
Сопр11 / РТМ+семинара++З+-+ДЗ3
.pdf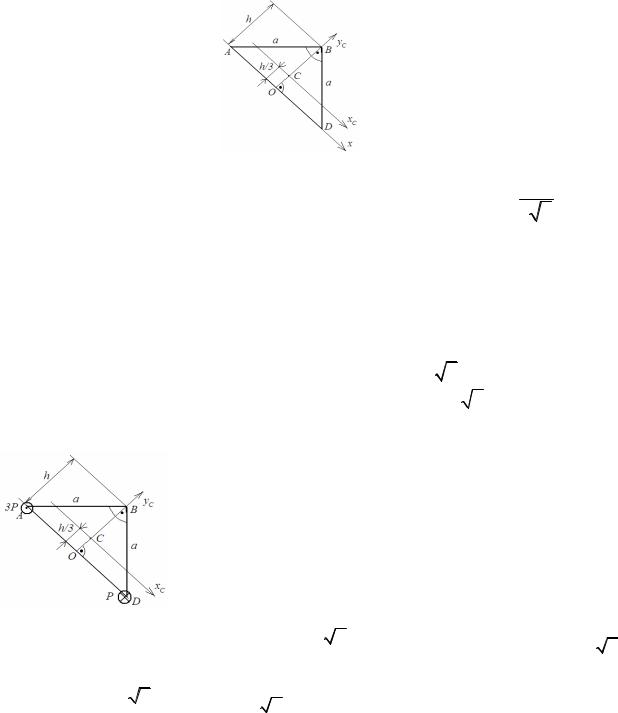
РУКОВОДЯЩИЙ ТЕХНИЧЕСКИЙ МАТЕРИАЛ СЕМИНАРА ПО ДЗ № 3
Тема семинара: косой изгиб, определение максимальных напряжений. Задача I типа. Внецентренное растяжение - сжатие
.
Этап 1. Расчет геометрических характеристик сечения
OYC – главная центральная ось инерции сечения.
В системе координат XOYC координата центра тяжести сечения ycC = h3 = 3 a2 .
Площадь поперечного сечения A = 1 a a = a2 .
2 2
По свойству аддитивности моментов инерции момент инерции сечения относительно центральной главной оси
I |
=2I |
|
|
|
h4 |
|
h4 |
a4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
yc +AOB |
=2 |
|
|
= |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
yc |
|
|
12 |
|
6 |
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2 |
|
AD h3 |
|
a2 |
|
a2 |
|
a 2 a3 |
|
a4 |
|
a4 |
|
|||
По теореме Штейнера |
Ix |
= Ix |
− yc |
A = |
|
− |
|
|
|
= |
|
|
− |
|
= |
|
. |
|||||||
12 |
18 |
2 |
12 |
2 2 |
36 |
72 |
||||||||||||||||||
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Этап 2. Приведение внешних сил к центру тяжести сечения С. 2.1. Расчетная схема приведения сил
2.2 . Теорема приведения системы сил к главному вектору R и главному моменту LC (теормех)
R = 2 P ; L x |
= −3 P |
h |
+ P |
h |
= −2 P |
h |
= − |
2 |
P a ; L y = 3 P h + P h = 4 P h = 2 2 P a. |
|
3 |
3 |
3 |
3 |
|||||||
|
|
|
|
|
|
2.3 Внутренние силовые факторы на всем участке (правила положительных знаков сопромата):
N = 2 P ; M x = |
2 |
P a ; |
M y = 2 2 P a. |
|
3 |
||||
|
|
|
1

2.4. Схема приложения внутренних силовых факторов.
Этап 3. Определение положения нейтральной линии в системе координат XCOYC
σ = |
N |
− |
M |
x |
y − |
M y |
x =0 (знаки напряжений по первому квадранту) |
A |
Ix |
|
Iy |
||||
|
|
|
|
|
|||
После подстановки 48 2x + 24 2 y = 4a . |
|||||||
Уравнение прямой в отрезках |
|
|
|
|
x |
|
|
|
+ |
|
|
y |
|
|
=1 - уравнение нейтральной линии |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
a |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
2 |
6 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Этап 4. Расчет максимальных напряжений. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Точка А. |
|
|
|
|
|
|
|
|
|
|
|
|
M y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
σ |
A |
= |
N |
|
− |
|
M |
x |
y |
A |
− |
|
x |
A |
= |
2P 2 |
+ |
|
|
2 72 |
Pa |
h |
+ |
2 2 24 |
Pah = |
P |
(4 |
+8 +48) |
=60 |
P |
||||||||||||||||||||||||
A |
|
|
Ix |
|
|
Iy |
|
a2 |
|
|
3a4 |
|
3 |
a4 |
a2 |
a2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Точка B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
σB |
= |
4P |
− |
|
|
2 72 |
Pa |
|
2a |
|
|
= −12 |
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
a2 |
|
|
|
3 |
2 |
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3a4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Точка С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
σ |
|
= 4 |
|
P |
|
|
+ |
|
|
2 72 |
Pa h |
− |
2 |
2 24 |
Pah = |
P |
(4 +8 −48) =−36 |
P |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
C |
a2 |
|
|
|
|
|
a2 |
a2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3a4 |
|
|
|
|
|
3 |
|
|
|
|
a4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Этап 5. Построение нейтральной линии и эпюры напряжений.
2

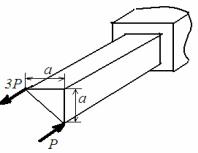
Задача 2-го типа. Нагрузки в двух взаимноперпендикулярных плоскостях
Рис.1
Решение.
Этап 1. Расчетные схемы изгиба в плоскостях XOZ и YOZ.
Рис.2 |
Рис.3 |
Этап 2. Построение эпюр изгибающих моментов Мx, Мy |
|
a) |
б) |
|
|
|
|
Рис.4 |
|
|
|
|
|
|
|
|
Рис.5 |
|
||
|
Уравнения равновесия: |
|
2 F; |
|
|
|
|
|
|
|
|
2 F; |
||||
а) |
∑MA =0 |
=RB 3l −2Fl |
→ RB |
= |
б) |
∑MA =0 =F 2l −RB 3l |
→ RB = |
|||||||||
|
|
|
|
|
3 |
|
2 |
|
|
1 |
3 |
|||||
|
∑Y =0 = |
2 |
|
|
|
4 |
|
∑Y =0 =F − |
|
|
|
|||||
|
|
F −2F +RA |
→ RA |
= |
|
F. |
|
|
F −RA |
→ |
RA = |
|
F. |
|||
|
3 |
3 |
|
3 |
3 |
|||||||||||
в) Эпюры изгибающих моментов в аксонометрии
Рис.6
г) Выбор наиболее опасных сечений №№ 1,2 – сечения с наибольшими изгибающими моментами в обеих плоскостях.
3
Этап 3. Геометрические характеристики сечений.
Ix |
= |
4a (2a)3 |
= |
8 |
4 |
; |
Iy = |
2a (4a)3 |
= |
32 |
a |
4 |
. |
12 |
3 |
a |
12 |
3 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
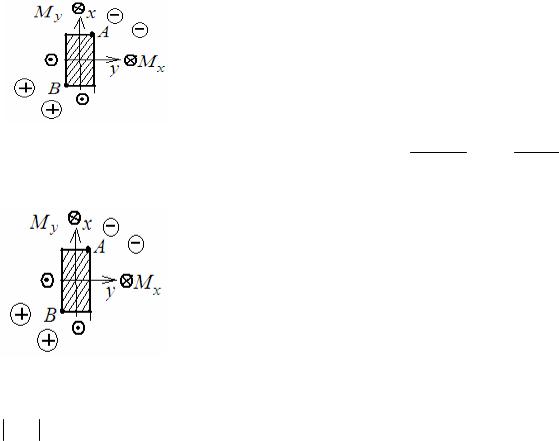
Этап 4. Расчет максимальных напряжений в точках наиболее опасных сечений.
σ z |
= − |
M y |
x − |
M |
x y; |
|
I y |
I x |
|||||
Сечение № 1 |
|
|
|
σ A = −σ B = − 34 Fl32a34 2a − 3Fl8a34 a = − 83 aFl4
σz |
= − |
M y |
|
x − |
M |
x y; |
|
|
|
|
|||||
Iy |
|
Ix |
|
|
|
|
|||||||||
Сечение № 2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2Fl 3 |
|
2Fl 3 |
|
3 Fl |
|||||
σ |
A |
= −σ |
B |
= |
2a + |
a = |
|||||||||
3 32a4 |
3 8a4 |
|
8 a3 |
||||||||||||
|
|
|
|
|
|
|
|||||||||
σmax = 83 Fla3
Этап 5. Расчет коэффициента запаса по текучести (σтр=σтс).
n |
= |
|
σ |
т |
= |
8 σ |
a3 |
|
|
т |
|
||||
σmax |
|
||||||
т |
|
|
3 Fl |
||||
4
