Фокусирующие системы / OPT_4-3

Богданов А.В. стр. 23 из 41 Фокусирующие системы ЛТУ

§ 1.4 ФОКУСЫ, ГЛАВНЫЕ ТОЧКИ И ФОКУСНЫЕ РАССТОЯНИЯ

ОПТИЧЕСКОЙ СИСТЕМЫ В ПАРАКСИЛЬНОЙ ОБЛАСТИ.

(т.1 с.23)

Рассмотрим три характерных положения предметной точки и ее изображения, имеющие большое значение при определении общих свойств оптических систем.

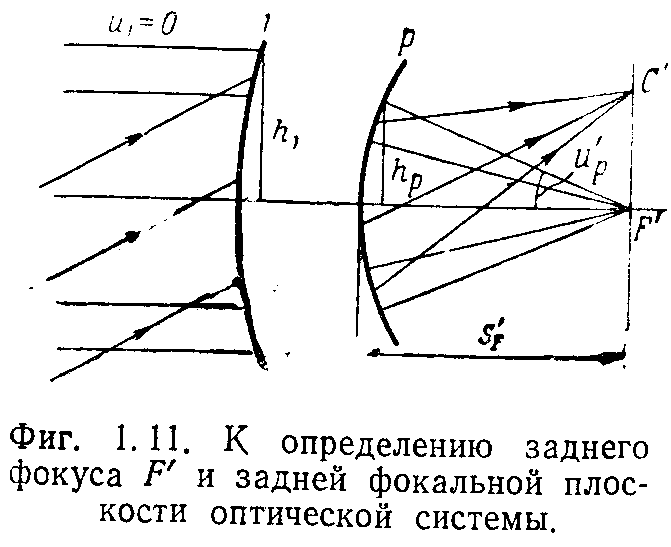
1 положение. Светящаяся точка находится на оптической оси слева в бесконечности (рис 1.11).Ее изображение будет в точке F'. Оно называется задним фокусом оптической системы. Пучок лучей из бесконечно удаленной точки на оси поступает в систему в виде пучка параллельных оптической оси лучей.

Следовательно, задний фокус обладает свойством что через него проходит всякий луч, поступающий в систему параллельно оси. Для нахождения положения заднего фокуса можно воспользоваться методом расчета хода лучей через оптическую систему, использовав для этого формулы (1.15) и (1.16) и положив для координат входного луча u = 0, а величину h выбрав произвольно. В результате получим значения h и u' = u ,после чего найдем отрезок s' , определяющий положение заднего фокуса:

(1.22)

Плоскость, проведенная перпендикулярно к оси через задний фокус, называется задней фокальной плоскостью; она является изображением бесконечно уделенной плоскости. Если светящаяся точка С, удаленная в бесконечность, находиться вне оптической оси, то лучи, идущие из нее, образуют наклонный пучок параллельных лучей, который имеет точку схода С' по выходе в задней фокальной плоскости (рис 1.11).

2 положение. Пусть светящаяся точка занимает такое положение на оптической оси F, что ее изображение находится справа в бесконечности. Эта точка называется передним фокусом оптической системы. Всякий луч, входящий в систему через передний фокус, выходит из системы параллельно ее оси (рис 1.12).

Для определения положения переднего фокуса можно так же воспользоваться формулами (1.15) и (1.16), применяя их в обратном порядке и положив , h выбирается произвольно. В результате будут найдены

Положение переднего фокуса определиться отрезком , равным

(1.23)

Плоскость, перпендикулярная к оптической оси и проходящая через передний фокус, называется передней фокальной плоскостью; ее изображение находится справа в бесконечности. Следовательно, пучок лучей, исходящий из любой точки С передней фокальной плоскости (коме фокуса), выходит из системы наклонным пучком параллельных лучей.

3 положение. Возьмем пару сопряженных и перпендикулярных к оптической оси плоскостей, для которых в параксильной области линейное увеличение равно +1.Такие плоскости называют передней и задней главными плоскостями, а точки их пересечения с оптической осью - главными точками. Обозначим их буквами Н и Н' (рис 1.13).

Пусть произвольный луч пересекает переднюю главную ось в какой-нибудь точке D. По выходе из оптической системы этот луч пересечет заднюю главную плоскость в точке D', которая будет изображением точки D. Эти точки удалены от оси системы на равные расстояния, т.к.

,

Отсюда следует, что входной и выходной лучи пересекают соответствующие главные плоскости на равных высотах.

Для луча, проходящего через главные точки, имеем:

; (1.24)

Положение главных плоскостей относительно фокусов определяется расстояниями f и f', которые соответственно называются передними и задними фокусными расстояниями. Фокусные расстояния отсчитываются от главных точек. Для определения этих расстояний опять воспользуемся формулами для расчета луча, проходящего через оптическую систему.

Возьмем произвольный луч, входящий в оптическую систему параллельно оптической оси u1=0 на высоте h1.

Этот луч выйдет из оптической системы через ее задний фокус под углом u' к оптической оси (рис 1.14)

Из рис 1.14 получим следовательно:

(1.25)

Положение заднего фокуса s'F и задней главной плоскости s'F относительно последней преломляющей поверхности определяется по формулам

(1.26); (1.27);

Аналогичным образом, применяя формулы (1.15) и (1.16) в обратном порядке, положив u'p =0 и взяв произвольное значение hp, можно определить переднее фокусное расстояние f, положения переднего фокуса sF и передней главной плоскости (рис 1.16).

(1.28)

(1.29)

(1.30)

Пусть теперь в систему падает наклонный пучок параллельных лучей под малым углом  w к ее оси (рис 1.16).Возьмем четыре луча из этого пучка и отметим их точки пересечения с передней главной плоскостью через D1 ,D2 ,D3 ,D4 .Преломляясь, эти лучи будут пересекать заднюю главную плоскость в точках D'1 ,D'2 ,D'3 ,D'4 удаленных от оси на такие же расстояния, как и точки D1 ,D2 ,D3 ,D4.(На рис 1.16 положение точек D'1 ,D'2 ,D'3 ,D'4 построено пунктирными линиями).Все эти лучи находятся в одной точке С' задней фокальной плоскости, удаленной от оси на расстояние dl'.

Рассматривая ход луча 1, проходящего через передний фокус, получим

wH (1.31)

и аналогично для луча 2, принимая во внимание формулу (1.24), будем иметь

(1.32)

Отсюда вытекает следующая зависимость между фокусными расстояниями оптической системы:

(1.33)

Т.к. всегда n > 0 и n'> 0, то, следовательно, фокусные расстояния оптической системы всегда имеют разные знаки. Обычно для характеристики оптической системы служит заднее фокусное расстояние, поэтому если f'>0, то система считается положительной, если f'< 0, то система считается отрицательной.

Если первая и последняя среды, окружающие оптическую систему, одинаковы, то при n = n’- f = f’,т.е. переднее и заднее фокусные расстояния равны друг другу, но противоположны по знаку. При этом из формулы (1.24) следует, что при

Всякий луч, входящий в оптическую систему через переднюю главную точку под некоторым углом, по выходе из системы проходит через заднюю главную точку под тем же углом, если последняя и первая среды одинаковы.

Таким образом, зная конструктивные элементы системы, с помощью формул (1.15) и (1.16) всегда можно определить фокусные расстояния, положение фокусов и главных плоскостей. Их расположение может быть самым различным в зависимости от того, какие конструктивные элементы имеет оптическая система.

Для иллюстрации на рис 1.17 показаны линзы различной формы с характерным положением главных плоскостей. Зная расположение фокусов и главных плоскостей в данной оптической системе, легко определить положение и величину изображения любого предмета, не рассматривая их последовательных изображений, как мы это делали раньше, что значительно упрощает решение задачи.

§ 1.5 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ И ВЕЛИЧИНЫ ИЗОБРАЖЕНИЯ, ОБРАЗУЕМОГО ОПТИЧЕСКОЙ СИСТЕМОЙ, У КОТОРОЙ ИЗВЕСТНЫ ПОЛОЖЕНИЯ ФОКУСОВ И ГЛАВНЫХ ТОЧЕК

(т.1 с.28)

Пусть дана оптическая система, состоящая из ряда преломляющих поверхностей, положения фокусов и главных плоскостей которой известны, а стало быть, известны и фокусные расстояния (рис 1.18).

Возьмем предмет dl, находящийся от переднего фокуса F системы 1-р на расстоянии х, а от передней главной точки Н на расстоянии а. Отрезки х и а имеют начало отсчета в точках F и Н.

Найдем положение изображения dl'.

Решим сначала эту задачу графическим способом. Построим изображение точки С - вершины заданного отрезка dl. Для этого достаточно взять любые два луча, выходящие из точки С, и найти точку их пересечения по

выходе из системы. Пусть луч СD идет параллельно оси, этот луч по выходе из системы пройдет через задний фокус F', причем у' = у = dl. Второй луч CF идет через первый фокус F и, следовательно, по выходе из системы будет параллелен оптической оси, при этом -y = -y' = -dl'. Точка С' пересечения этих лучей определяет положение и величину изображения отрезка dl'.

Из подобия треугольников получим

 (1.34)

откуда

(1.35)

или, заменяя х = a - f и x' = a'- f', найдем

(1.36)

Формулы (1.35) и (1.36) дают возможность определить положение изображения, зная положение предмета. Формула (1.35) носит название формулы Ньютона, а формула (1.36) - Гаусса.

Проведем теперь луч из точки А под некоторым углом к оси через точку D. Из фигуры следует, что

u = Y/a , u'= Y'/a'= Y/a'

Если теперь воспользоваться формулами (1.14) и (1.34), то получим следующую формулу для линейного увеличения:

 (1.37)

Таким образом, по формуле (1.37) можно вычислить величину изображения:

dl' = dl

Положение же изображения относительно последней преломляющей поверхности S' определяется с помощью формул (1.35) и (1.36), а именно:

S'= S'F + x'

или

S' = S'H + a'

Таким образом, если имеется сложная оптическая система с заданными конструктивными элементами и требуется найти положение и величину изображений ряда по разному расположенных предметов, то выгоднее сначала найти положение фокусов и главных плоскостей, а затем уже решать поставленные задачи по методике, изложенной в данном параграфе.

Кафедра МТ12 7^ой семестр opt_4-3.doc