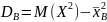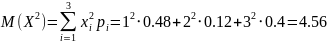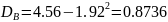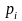45вариант_DDZ
.docxВариант 45
Задание 1
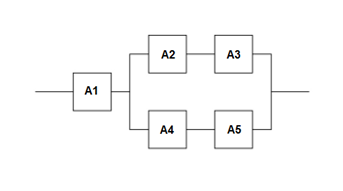
Электрическая цепь состоит из пяти элементов, выход из строя которых в заданный промежуток времени – независимые события, имеющие вероятности pi = 0.1 каждый. Найти вероятность Р отказа цепи за данный промежуток времени.
Решение
Рассмотрим порядок соединения для получения приведенной электрической схемы.
1. Элемент 1 и участок 2-5 соединены последовательно в участок 1-5.
2. Участки 2-3 и 4-5 соединены параллельно в участок 2-5.
3. Элементы 2,3 и 4,5 соединены последовательно.
Введем следующие обозначения событий:
Ai – работает элемент i (i=1, 2, …, 5),
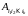 –
работает
участок соединения из элементов
–
работает
участок соединения из элементов
 .
.
По условию задачи
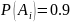
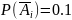
Необходимо
найти вероятность события
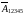 .
.
Будем находить вероятности событий, перечисленных в порядке соединения схемы.
При этом будем помнить, что для параллельного соединения проще найти вероятность отказа участка (все элементы соединения не работают), а для последовательного соединения проще найти вероятность работы участка (все элементы соединения работают).
Eсли соединение последовательное, нужно перемножать события, то есть
X=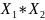
X1 - работает первая группа элементов X2 - работает вторая группа элементов
Теперь рассмотрим каждую группу. В первой группе всего один элемент, то есть она работает, когда работает первый элемент цепи (X1=A1). Мы дошли до элемента, разбор этой группы закончен.
Рассмотрим вторую группу. Видно, что вторая группа имеет уже параллельную структуру элементов. А вот внутри A4⋅A5 элементы соединены последовательно, A2⋅A3 элементы также между собой последовательно.
Так как A4⋅A5 и A2⋅A3 группа соединены параллельно, речь идет о сумме этих событий, то есть вторая группа работает если:
X2=A2⋅A3+A4⋅A5.
Сводим все в одну формулу и выпишем искомое событие (Цепь работает исправно):
X=X1⋅X2=A1⋅(A2⋅A3+A4⋅A5).
Надо определить вероятность того, что ток проходит в цепи. Будем использовать формулы (1-3).
P(A⋅B)=P(A)⋅P(B); (1)
P(A+B)=P(A)+P(B)−P(A)⋅P(B); (2)
P(A1+A2+...+An)=1−P(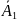 )⋅P(
)⋅P(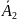 )⋅...⋅P(
)⋅...⋅P(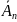 ).
(3)
).
(3)
Так как вероятность произведения для независимых событий равна произведению вероятностей, получим:
P(X)=P(A1⋅(A2⋅A3+A4⋅A5))==P(A1)⋅P(A2⋅A3+A4⋅A5)=
Для множителей с суммой событий внутри используем формулу (2):
=P(A1)⋅[P(A2⋅A3)+P(A4⋅A5)−P(A2⋅A3⋅A4⋅A5)]=
И снова раскрываем вероятности произведений:
=P(A1)⋅[P(A2)⋅P(A3)+P(A4)⋅P(A5)−P(A2)⋅P(A3)⋅P(A4)⋅P(A5)].
Перейдем к более компактной записи, положив pi=P(Ai)
P(X)=p1⋅[p2⋅p3+p4⋅p5−p2⋅p3⋅p4⋅p5].
Вероятность работы цепи:

Мы нашли вероятность работы цепи. Вероятность отказа:
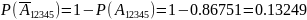
Ответ: 0.13249.
Задание 2
Дискретная случайная величина задана законом распределения pi(xi). Найти величину a, построить график функции распределения данной случайной величины. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины.
|
0 |
2 |
4 |
6 |
8 |
|
|
0,2 |
0,4 |
0,2 |
0,1 |
Решение
Так как сумма вероятностей должна быть равна 1, то величина а равна:
а = 1 – (0.2 + 0.4 + 0.2 + 0.1) = 0.1
Найдем функцию распределения:
Для нахождения интегральной функции распределения пользуемся ее определением применительно к каждому из промежутков изменения с.в.
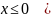
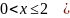
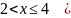
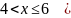
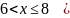

Вид функции распределения:
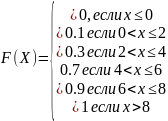
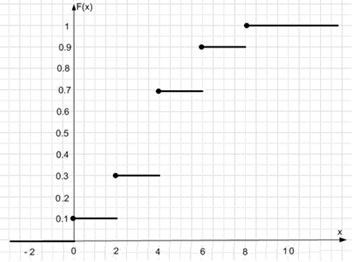
График функции распределения:
Математическое ожидание:
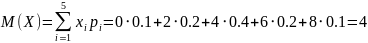
Найдем дисперсию:
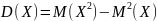

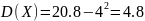
Среднее квадратическое отклонение:

Задание 3
Плотность распределения вероятностей непрерывной случайной величины задана выражением:
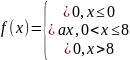
Найти величину коэффициента а, написать аналитическое выражение и простроить график функции распределения, найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. Найти вероятности попадания данной случайной величины в интервалы (0,6) и (6,10).
Решение
Найдем коэффициент a из условия:
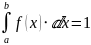
Для нашей функции:
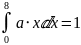
 или
или
32·a-1 = 0
Откуда, a = 1/32
Найдём функцию распределения:
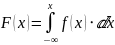
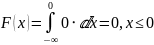
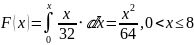
F(x) = 1, x > 8
Найдем математическое ожидание:
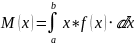
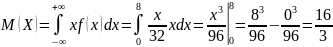
Найдём дисперсию непрерывной случайной величины Х:
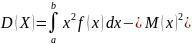
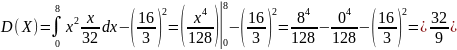
Среднее квадратическое отклонение:
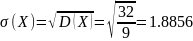
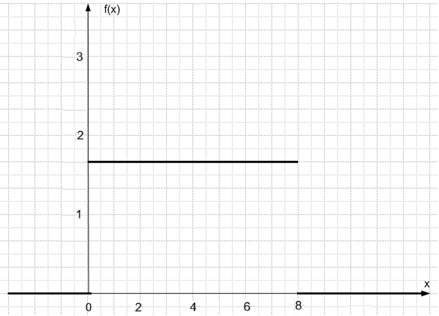
График плотности распределения:
Вероятность попадания непрерывной случайной величины в интервал найдем по формуле:
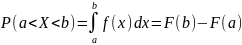
Поэтому:
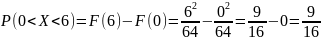
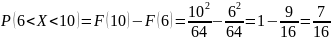
Задание 4
Вероятность попадания нормально распределенной случайной величины с математическим ожиданием m = 5 в интервал (4; 6) равна 0,8. Найти дисперсии данной случайной величины.
Решение
Для нормального распределения вероятность попадания случайной величины в интервал определяется по формуле:
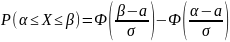
где Ф(Х) – функция Лапласа, значения которой определяются по таблицам,
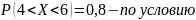
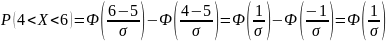 +
+
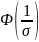 =2
=2
2
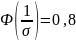
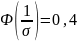
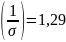

Найдём дисперсию:
D(X)=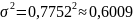
В данном случае:

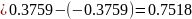
Ответ:
D(X)
Задание 5
Дискретная случайная величина задана выборкой:
1, 2, 3, 3, 3, 3, 3, 1, 1, 1, 2, 3, 3, 1, 1, 1, 1, 3, 3, 1, 1, 1, 2, 3, 1
Построить полигон частот и эмпирическую функцию распределения. Найти выборочное среднее и выборочную дисперсию.
Решение
Составим ряд распределения в виде таблицы:
xi |
1 |
2 |
3 |
ni |
12 |
3 |
10 |
Строим полигон частот:
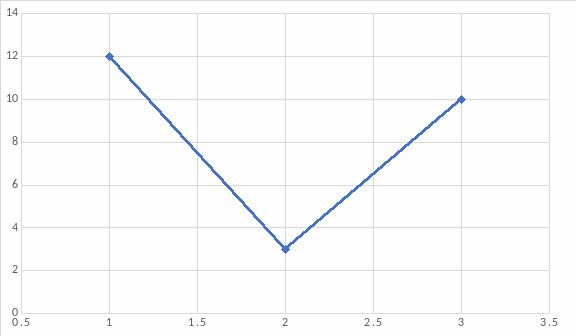
![]()
![]()
Находим относительные частоты:
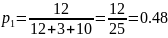
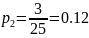
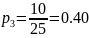
Тогда функция распределения:
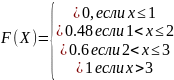
График функции распределения:
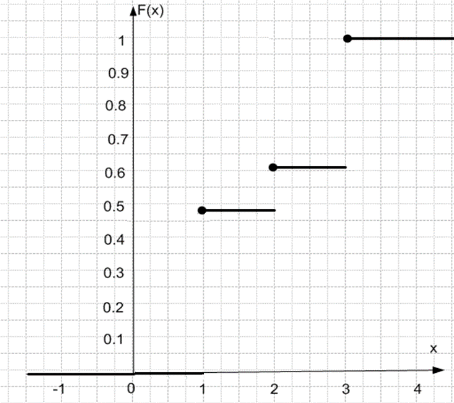
Выборочное среднее:
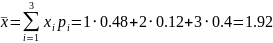
Найдем выборочную дисперсию: