Informatika(Логика, програмирование) / Использование графов при решении задач

Использование графов при решении задач

Вашему вниманию представлены теоретический материал, примеры решения задач и упражнения для тренировки по теме «Использование графов при решении задач». Рекомендуем работать с текстом лекции следующим образом. Прочитайте условие задачи и попробуйте решить её самостоятельно, после чего внимательно прочитайте решение. Если Вы получили правильный ответ, но Ваше решение отличается от предложенного, подумайте, всё ли Вы учли в своём решении. Оцените время и усилия, которые потребовались в каждом способе, и выберите тот, который Вам более понятен и быстрее приводит к результату. Для закрепления материала выполните упражнения. Задачи не связаны между собой, поэтому их изучение можно вести в любом порядке. Курсивом в решении выделены теоретические сведения, которые нужны для понимания решения, но их не нужно каждый раз записывать в тексте решения.

Решение некоторых задач значительно упрощается, если условие или ход рассуждений наглядно изобразить в виде графа. Под графом будем понимать некоторое множество точек и отрезков, соединяющих эти точки. Точки называются вершинами графа, отрезки – ребрами графа. Циклом в графе называется такая последовательность вершин и ребер, в которой все ребра различны, а начальная и конечная вершина совпадают. Граф, в котором отсутствуют циклы, называется деревом.

Задача 1.

В таблицах приведена протяженность магистралей между соседними населенными пунктами. Если пересечение строки и столбца пусто, то соответствующие населенные пункты не соединены автомагистралями. Укажите номер таблицы, для которой выполняется условие: «Максимальная протяженность маршрута из пункта A в пункт C не больше 5». (Протяженность маршрута складывается из протяженности автомагистралей между соответствующими соседними населенными пунктами.)

1

. Для каждой из таблиц изобразим схематично маршруты в виде графа, в котором вершинами являются населенные пункты, а ребрами – автомагистрали. Рядом с каждым ребром

Вычислим для каждого графа длины всех возможных маршрутов из А в С:

1)ABC – 3, ADC – 5, ABDC – 8;

2)AC – 2, ABC – 3, ABDC – 6;

3)AC – 3, ABC – 4, ADBC – 6;

4)AC – 2, ABC – 5, ADC – 2.

Вкаждом случае подчеркнута максимальная длина маршрута. Очевидно, максимальная протяженность не превосходит 5 только в одном случае – для четвертой таблицы.

Ответ: 4.

Упражнение 1.

Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечении строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними станциями. Если пересечение строки и столбца пусто, соответствующие станции не являются соседними. Укажите таблицу, для которой выполняется условие: «Минимальная стоимость проезда из A в B не больше 6». (Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями.)

Упражнение 2.

В таблице задана стоимость перевозок между соседними железнодорожными станциями. Укажите схему, соответствующую таблице.

2

QLO в этот день он опоздает, поэтому этот маршрут окажется самым невыгодным. Из двух оставшихся маршрутов самое раннее время прибытия даёт путь с пересадкой в IGT.

Ответ: 15:40.

Упражнение 3.

Между четырьмя местными аэропортами: ОКТЯБРЬ, БЕРЕГ, КРАСНЫЙ и СОСНОВО, ежедневно выполняются авиарейсы. Приведён фрагмент расписания перелётов между ними:

Путешественник оказался в аэропорту ОКТЯБРЬ в полночь (0:00). Определите самое раннее время, когда он может попасть в аэропорт СОСНОВО.

Задача 3.

На месте преступления были обнаружены четыре обрывка бумаги. Следствие установило, что на них записаны фрагменты одного IP-адреса. Криминалисты обозначили эти фрагменты буквами А, Б, В и Г. Восстановите IP-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.

А) 2.131 Б) 20 В) .31 Г) 2.19

Решение. 32-разрядные IP-адреса разбиваются на четыре группы по 8 бит, каждая группа представляется десятичным числом от 0 до 255, числа записываются через точку.

Для решения будем использовать граф, в котором вершинами являются фрагменты адреса. Вершины будем соединять ребром, если взятые фрагменты могут в адресе стоять рядом. При этом стрелкой на ребре будем отмечать направление, в котором фрагменты могут следовать друг

за другом. Найдем вершину, в которую не входит ни одной стрелки (Б) – это будет первый фрагмент адреса. Вершина, из которой не выходит ни одной стрелки (В) – последний фрагмент. Поскольку между оставшимися двумя вершинами стрелка только одна, то получаем ответ.

Ответ: БГАВ.

4

Упражнение 4.

На месте преступления были обнаружены четыре обрывка бумаги. Следствие установило, что на них записаны фрагменты одного IP-адреса. Криминалисты обозначили эти фрагменты буквами А, Б, В и Г. Восстановите IP-адрес. В ответе укажите последовательность

Задача 4.

Два игрока играют в следующую игру. На координатной плоскости стоит фишка. Игроки ходят по очереди. В начале игры фишка находится в точке с координатами (5, 2). Ход состоит в том, что игрок перемещает фишку из точки с координатами (x, y) в одну из трех точек: или в точку с координатами (x+3, y), или в точку с координатами (x, y+3), или в точку с координатами (x, y+4). Выигрывает игрок, после хода которого расстояние по прямой от фишки до точки с координатами (0, 0) не меньше 13 единиц. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.

Решение. Под игрой понимается процесс, в котором участвуют две (или более) стороны, ведущих борьбу за реализацию своих интересов. Каждая из сторон имеет свою цель – выигрыш, но выигрыш или проигрыш зависит не только от действий самого игрока, но также от поведения других игроков. Позиция в игре – это состояние объектов, участвующих в игре (например, расположение фигур). Начальная позиция – это состояние, с которой начинается игра. Конечная (или терминальная) позиция – это позиция, в которой заканчивается игра. Стратегия игрока – это последовательность ходов, ведущих из начальной позиции в конечную. Обычно в игре из любой позиции возможны несколько вариантов хода игрока, то есть игрок располагает множеством стратегий. Построение выигрышной стратегии заключается в выборе такого хода, который (если это возможно) ведёт к выигрышу. Безошибочная (правильная) игра заключается в том, что если у игрока есть возможность добиться выигрыша, следуя какой-либо стратегии, то он будет выбирать ходы в соответствии с этой стратегией.

Ход игры можно изобразить в виде графа, в котором вершинами будут позиции игры, а ребрами – ходы игроков. Поскольку в игре нет возможности вернуться в какую-либо позицию, то в графе игры отсутствуют циклы, то есть он является деревом.

5

Любую позицию в рассматриваемой игре можно описать парой чисел, соответствующих координатам точки. Расстояние L от точки с координатами (x, y) до начала координат

равно квадратному корню из суммы квадратов координат: L = x2 + y2 , значит, условие

окончания игры запишется как L ≥ 13. Заметим, что можно не вычислять квадратный корень, если перейти от условия L ≥ 13 к равносильному условию в целых числах: L2 ≥132 =169 . Для удобства отслеживания момента окончания игры будем для каждой позиции игры также указывать значение L2 (мелким шрифтом).

В начальной позиции L2 = 52 + 22 = 25+ 4 = 29 , условие окончания игры не выполнено, значит, первый игрок должен сделать ход, причем у него есть три варианта хода. Для наглядности построим дерево игры. Заметим, что ход игры можно оформлять также в виде таблицы. При оформлении решения не нужно рисовать дерево и таблицу, – достаточно выбрать один из вариантов оформления, который Вам больше понятен.

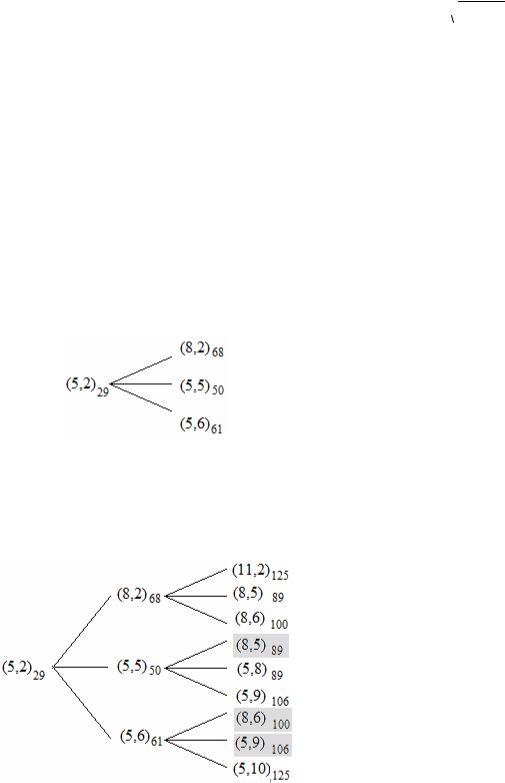
Видим, что одним ходом первый игрок никак не может выиграть (для всех вариантов L2<169). Поэтому рассмотрим следующий ход – второго игрока.

Серым выделены варианты, которые уже встречались в качестве результата второго хода (хотя получены в результате другой последовательности ходов). Дальше не стоит их рассматривать отдельно.

6

Проанализируем результаты второго хода. Очевидно, второй игрок тоже никак не может выиграть (для всех вариантов L2<169). Поэтому продолжаем рассуждения для третьего хода (его снова делает первый игрок). Поскольку дерево «разрастается» довольно быстро, то для сокращения записей мы не будем указывать все варианты хода, если из какой-то позиции существует ход, ведущий к выигрышу (будем указывать только этот вариант хода). Выигрышную позицию будем выделять жирным и подчёркивать.

В виде графа:

В виде таблицы:

Видим, что в некоторых случаях первый игрок может выиграть уже после третьего хода, однако для этого второй игрок должен выбрать варианты хода, ведущие к выигрышу первого игрока. Но поскольку второй игрок стремится к выигрышу (как и первый) на втором

7

ходе игры он не будет выбирать те варианты хода, которые ведут к выигрышу первого игрока, если у него есть возможность выиграть. А это мы сможем узнать, только рассмотрев дальнейший ход игры.

В виде графа:

В виде таблицы:

Теперь осталось выполнить самое главное – сделать анализ полученного дерева (таблицы) и определить, кто же выиграет, если оба играют лучшим для себя образом. Докажем, что выигрывает второй игрок (на четвертом ходе игры) при любом варианте ходов первого игрока. Какой бы первый ход ни сделал первый игрок, на втором ходе второй игрок может получить позицию (8,5) или (8,6). Из этих двух позиций первый игрок никаким своим ходом не может попасть в выигрышную позицию. А далее при любом ходе первого игрока (третий ход

8

игры) четвертым ходом второй игрок всегда может выиграть, если будет выбирать позиции, указанные в дереве игры (таблице).

Таким образом, при правильной игре выигрывает второй игрок.

Осталось выяснить, какой вариант первого хода должен выбрать второй игрок, чтобы свести игру к своему выигрышу:

(5,2) → (8,2) → (8,5) или (8,6) (5,2) → (5,5) → (8,5)

(5,2) → (5,6) → (8,6)

Замечаем, что второму игроку первым своим ходом нужно изменять ту координату, которая осталась неизменной после хода первого игрока.

Ответ: выигрывает второй игрок, для этого ему первым своим ходом нужно изменить ту координату, которая осталась неизменной после хода первого игрока.

Возможные ловушки и проблемы:

•Таблица получается довольно громоздкой, чтобы не запутаться, лучше оставлять в ней только те данные, которые действительно влияют на решение (как мы делали выше).

•Обнаружив, что первый игрок выигрывает в некоторых вариантах на 3-ем ходу, можно (напрасно!) обрадоваться и записать неверный ответ (помните, что факт выигрыша в ка- ких-то случаях, еще не означает, что этот игрок выиграет всегда).

•Для обоснования ответа необходимо проверить, при любом ли ходе проигрывающего игрока выигрывающий игрок может получить нужную для себя ситуацию.

•Обращайте внимание на формулировку условия окончания игры. Оно может быть сформулировано в виде «проигрывает тот игрок, после хода которого … ». В этом случае конечные позиции в дереве игры означают не выигрыш, как в рассмотренной задаче, а проигрыш. И при выборе выигрывающего игрока нужно учитывать неподчеркнутые конечные позиции.

Упражнение 5.

Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 1 камень, а во второй - 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то кучке, или добавляет 3 камня в какую-то кучку. Выигрывает игрок, после хода которого в одной из кучек становится не менее 24 камней. Кто выигрывает при безошибочной игре - игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.

9

Ответы и решения к упражнениям

Упражнение 1.

Для каждой из таблиц изобразим схематично маршруты в виде графа, в котором вершинами являются станции, а ребрами – дороги между ними. Рядом с каждым ребром укажем стоимость проезда между соответствующими пунктами.

1) 2) 3) 4)

Вычислим для каждого графа стоимости всех возможных маршрутов из А в В:

1)ACB – 7, ACЕВ – 7;

2)ACВ – 7, AЕCВ – 7;

3)ACВ – 7, ACЕВ – 6;

4)ADCB – 9, ADCEB – 8.

Вкаждом случае подчеркнута минимальная стоимость. Очевидно, минимальная стоимость не превосходит 6 только в одном случае – для третьей таблицы.

Ответ: 3.

Упражнение 2. Ответ: 2.

Упражнение 3.

Изобразим схематично маршруты в виде графа, в котором вершинами являются аэропорты, а ребрами – авиалинии. Для сокращения записи на рисунке будем обозначать аэропорты по первой букве названия. Поскольку нас интересует перелет из O в C, то стрелками отметим те маршруты, которые позволяют осуществить этот перелет.

По рисунку видим, что имеется три маршрута. Выбрав прямой рейс из О в С, путешественник окажется в С в 17:25. Рассмотрим маршрут О–Б–С: в Б путешественник окажется в 17:15, и на рейс Б–С в этот день он опоздает, поэтому этот маршрут окажется невыгодным. Для маршрута О–К–С: в К

путешественник прилетит в 13:30, и на рейс К–С в этот день он опоздает, поэтому этот маршрут окажется также невыгодным. Остается единственный маршрут – напрямую из О в С.

Ответ: 17:25.

10