3.2. Простейшие элементы механических систем

Пусть величина υ проекции скорости скольжения тела на выбранную координатную ось Ox пропорциональна величине P проекции приложенной силы на эту ось (рис. 8), тогда

P = kТРSυ ,

где kтр — коэффициент вязкого (линейного) трения, измеряемый в Н c /м3 ; S — площадь поверхности контакта.

Рис. 8. Схема скольжения тела по поверхности

Если в качестве потенциальной величины выбрать величину P, а в качестве потоковой

— величину υ, то записанное равенство можно сопоставить с уравнением состояния резистора. Тогда аналогами падения электрического напряжения и силы тока являются величины P и υ соответственно. Аналогом электрического сопротивления является величина RМ = kТРS . Величину RМ измеряют в кг/c , так как единицами измерения силы и скорости

являются соответственно Н = кг м/с2 и м/c .

Пусть величина ω проекции угловой скорости вращения цапфы вала (рис. 9) на ось вращения пропорциональна величине M проекции вращающего момента на эту ось, тогда

M = kТР 2π r l r 2 ω = 2π kТР r3 l ω ,

где M — величина, измеряемая в Н м; ω — величина, единицей измерения которой является рад/с; r и l — радиус и длина цапфы соответственно.

Рис. 9. Схема вращения цапфы вала относительно вкладыша подшипника: 1 — цапфа вала; 2 — вал; 3 — вкладыш подшипника скольжения; 4 — подшипник скольжения

Если в качестве потенциальной величины выбрать величину M, а в качестве потоковой — величину ω, то аналогами падения электрического напряжения и силы тока являются величины M и ω соответственно. Аналогом электрического сопротивления является величина RМo = 2π kТР r3 l , измеряемая в Н м с.

39

При относительном перемещении отдельных элементов механической системы на поверхности их контакта возникают силы трения, препятствующие этому перемещению. При движении против сил трения совершается работа. Мощность, требуемая для преодоления

трения при поступательном движении, равна WТР = Pυ = RМ υ2 , а при вращательном — WТР = Mω = RМo ω2 . Эта мощность является аналогом мощности тепловыделения на резисто-

ре.

В технических устройствах различного назначения часто используют узлы крепления. Такую механическую связь характеризуют жесткостью, под которой понимают отношение силы, приложенной к такому узлу, к перемещению точки приложения этой силы. Далее рассмотрим простейшую схему узла крепления (рис. 10).

Рис. 10. Схема узла крепления детали к неподвижному основанию: 1 — деталь; 2 — неподвижное основание; 3 — пружина

Пусть деталь крепится к неподвижному основанию с помощью пружины, жесткость которой равна c. Жесткостью пружины называют отношение c = P / u , измеряемое в

Н/м = кг/с2 , где P — величина проекции силы на координатную ось Ox инерциальной сис-

темы отчета; u — перемещение точки приложения силы, причем при u = 0 пружина не деформирована. Изменение во времени t силы приведет к изменению перемещения u. Если пренебречь массой пружины, а значение c считать постоянным, то после дифференцирования левой и правой частей равенства u(t) = P(t)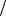c по времени получим

где υ — проекция скорости перемещения точки приложения силы; CМ =1/ c — податливость пружины, измеряемая в м/Н. Величину CМ можно рассматривать как аналог емкости электрического конденсатора. Очевидно, что величины u и υ являются аналогами электриче-

ского заряда Qe конденсатора и силы электрического тока I = ddQte соответственно.

При растяжении или сжатии пружины величина потенциальной энергии П равна работе силы, совершаемой при перемещении точки приложения этой силы. Если считать, что при u = 0 потенциальная энергия пружины равна нулю, то

Эта энергия является аналогом энергии электрического поля в конденсаторе. Полученные зависимости (27) и (28) характерны для многих элементов, материал которых при нагружении сохраняет свойство линейной упругости.

40

Если рассмотреть растяжение линейно упругого невесомого стержня с поперечным сечением площадью S (рис. 11), то в соответствии с законом Гука относительная деформация стержня равна

ε = σE = EPS ,

где σ = P / S — механическое напряжение в поперечном сечении стержня; E — модуль упругости материала стержня при растяжении (модуль Юнга), измеряемый в паскалях Па = Н/ м2 .

Рис. 11. Схема растяжения линейно упругого стержня

При этом торец стержня, подверженный действию силы, переместится относительно закрепленного торца на расстояние

u = ε l = EPSl ,

где l — начальная длина стержня. Тогда после дифференцирования левой и правой частей этого равенства по времени получим

величина является аналогом емкости электрического конденсатора.

Затем рассмотрим кручение упругого невесомого стержня длиной l (рис. 12).

Рис. 12. Схема кручения упругого стержня

41

Если один из концов упругого стержня жестко закреплен, а ко второму приложен крутящий момент, то угол закручивания стержня будет

ϕ= Мкр l ,

G J p

где Mкр — величина проекции крутящего момента на ось кручения; G — модуль сдвига материала стержня, который измеряют в Па; Jp — полярный момент инерции сечения стержня, единицей измерения которого является м4.

Для стержня с круглым поперечным сечением диаметра d полярный момент инерции равен π d 4 / 32 . Произведение величин G и Jp называют жесткостью сечения при кручении.

Дифференцированием по времени t находим

где ω — проекция на ось кручения угловой скорости поворота конца стержня, к которому приложен крутящий момент; CМo = GlJ p — податливость упругого стержня при кручении.

Эту величину измеряют в Н1м .

Если в качестве потенциальной величины выбрать величину Mкр, а в качестве потоко-

вой — величину ω, то аналогами падения электрического напряжения и силы тока являются величины Mкр и ω соответственно. Тогда величину CМo можно рассматривать как аналог ем-

кости электрического конденсатора.

Таким образом, при различном выполнении упругих элементов механической системы можно установить зависимости, аналогичные уравнению состояния электрического конденсатора.

Соотношение, аналогичное уравнению состояния индуктивной катушки можно получить непосредственно из второго закона Ньютона. Действительно, в случае поступательного движения тела массой m, к которому приложена сила, справедливо

P = m ddυt ,

где P — величина проекции силы на выбранную координатную ось инерциальной системы отчета; υ — величина проекции на эту ось скорости тела.

Если в качестве потенциальной величины выбрать величину P, а в качестве потоковой

— величину υ, то записанное равенство можно сопоставить с уравнением состояния индуктивной катушки. Тогда аналогом индуктивности катушки является масса тела.

В случае вращения тела относительно фиксированной оси под действием вращающего момента относительно этой оси справедливо

M = J ddωt ,

где M — величина проекции момента на ось вращения; J — момент инерции тела относительно оси вращения; ω — проекция на ось вращения угловой скорости. Если в качестве потенциальной величины выбрать величину M, а в качестве потоковой — величину ω, то аналогом индуктивности катушки является момент инерции тела относительно оси вращения, измеряемый в кг м2 .

42