5.4. Простейшие динамические модели

Если ММ описывает механическое движение тел как результат взаимодействия между телами, то такую модель называют динамической. Термины “динамическая ММ”, “нестационарная ММ” и “эволюционная ММ” обычно используют как синонимы.

Рассмотрим построение нелинейной динамической модели на примере простейшей механической системы с одной степенью свободы (рис. 54).

Рис. 54. Простейшая механическая система

Пусть механическая система состоит из всего одной материальной точки массой m. Состояние такой системы в момент времени t характеризуют значения перемещения u(t) материальной точки и ее скорости υ(t). На материальную точку действуют две силы, проекции которых на положительное направление координатной оси Ou обозначим P и P . Первая из сил — стационарная потенциальная сила1. Она не зависит от скорости υ и является функцией лишь перемещения u, т.е. P = P(u) . Вторая сила — непотенциальная, для нее в общем

случае имеем P = P (u, υ, t) . Согласно второму закону Ньютона запишем

Таким образом, скорость изменения кинетической энергии равна мощности действующих на материальную точку сил, что следует из закона сохранения энергии.

Очевидно, что для потенциальной энергии П(u) данной системы справедливо

P(u) = − d П(u) . d u

Тогда после подстановки

− P(u)υ = ddПu ddut = ddПt

в уравнение (63) получим

1 Силы называют потенциальными, если работа этих сил при переходе механической системы из одного положения в другое не зависит от пути и равна уменьшению потенциальной энергии системы (при мгновенном перемещении из одного положения в другое). Если потенциальные силы являются стационарными, то требование, заключенное в скобки, несущественно. К потенциальным силам относят, например, силу тяжести и реакцию упругих связей.

98

где W = К+ П — полная энергия системы.

В этом случае скорость изменения полной энергии W равна мощности P (u, υ, t)υ не-

потенциальной силы, действующей на рассматриваемую систему. В случае консервативной системы мощность непотенциальной силы равна нулю и W = К+ П = const .

Если в формуле (64) P (u, υ, t)υ ≤ 0 , то полная энергия динамической системы

уменьшается (рассеивается) за период времени, в течение которого мощность непотенциальной силы принимает отрицательные значения. Такую систему называют диссипативной (от латинского слова dissipatio — рассеяние). При этом механические формы энергии могут переходить в немеханические, например, в тепловую энергию.

Периодические колебания механической системы возможны, если ее полная энергия остается неизменной (как, например, в случае консервативной системы). Движение диссипативной системы не может быть периодическим. Строго говоря, полная энергия большинства реальных систем не остается постоянной. Поэтому динамические ММ консервативных систем лишь приближенно описывают поведение реальных систем.

Если действующие на механическую систему силы не зависят явно от времени, то ее называют автономной системой. Этот термин согласуется с понятием автономной нормальной системы ОДУ, которая описывает движение рассматриваемой механической системы и состоит из следующих уравнений:

Такая система ОДУ в общем случае является нелинейной динамической ММ данной механической системы.

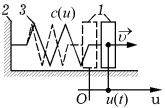
Пример 1. В качестве автономной механической системы рассмотрим твердое тело 1 массой m, движущееся по горизонтальной поверхности при наличии трения и связанное с неподвижной опорой 2 пружиной 3, жесткость c которой зависит от перемещения u этого те-

ла (рис. 55).

Рис. 55. Схема механической системы: 1 — тело; 2 — неподвижное основание; 3 — пружина

Отсчет перемещения u удобно вести от положения, в котором пружина не деформирована. Пружина действует на тело силой, являющейся потенциальной, причем проекция этой силы на положительное направление координатной оси Ou равна

P(u) = −c(u)u .

Предположим, что проекция P на положительное направление координатной оси силы трения пропорциональна квадрату скорости υ, т.е.

P (υ) = −kυ2 sgnυ ,

где k = const > 0 — коэффициент пропорциональности; sgnυ — функция-сигнум (знак).

99

Согласно второму закону Ньютона получим

m ddυt = P(u) + P (υ) = P(u) − kυ2 sgnυ .

Тогда движение рассматриваемой механической системы описывает автономная нормальная система ОДУ

Потенциальную энергию этой системы можно установить по формуле

u

П(u) = −∫P(s) d s ,

u0

где u0 — некоторое значение, определяющее положение тела, в котором потенциальную энергию полагают равной нулю. Тут удобно считать, что u0 = 0 , т.е. u0 равно значению, оп-

ределяющему положение тела, в котором пружина не деформирована. В этом случае для полной энергии системы получим

т.е. рассматриваемая система является диссипативной. При этом система за счет уменьшения своей полной энергии совершает работу против силы трения, частично или полностью переходящую в теплоту.

Если силой трения можно пренебречь, т.е. положить k = 0 в формуле (65), то ddWt = 0 ,

что соответствует консервативной системе, а ее динамическая ММ может описывать периодические колебания твердого тела.

Если принять скорость в качестве потоковой величины, а действующие силы — в качестве потенциальных, то введенные для механической системы понятия и полученные соотношения можно перенести на другие технические системы, в которых протекают процессы немеханической природы.

Пример 2. Рассмотрим на рис. 56 электрическую цепь, состоящую из катушки индуктивности L, конденсатора емкости C и резистора, сопротивление R(I) которого зависит от силы I тока в контуре.

Рис. 56. Электрическая цепь

100

При достаточно длительном подключении к контуру источника напряжения (ключ К в положении 1) конденсатор накопит электрический заряд Qe пропорционально разности потенциалов U* на его обкладках, причем

Qe = CU .

Очевидно, что энергия электрического поля, запасенная в конденсаторе, равна

Пусть в некоторый момент времени t = t0 ключ К переведен из положения 1 в положение 2. Тогда, согласно второму закону Кирхгофа, имеем

где Qe (t) — электрический заряд конденсатора в момент времени t. Учитывая, что

I = ddQte ,

запишем автономную нормальную систему ОДУ

которая является нелинейной ММ данной электрической системы.

Если принять первый вариант электромеханической аналогии, то кинетической энергии соответствует энергия магнитного поля катушки, а потенциальной — энергия электрического поля, запасенная в конденсаторе. Это позволяет перенести полученные ранее соотношения для механической системы на электрическую систему. Действительно, полная энергия рассматриваемой электрической системы равна

Учитывая равенство (66), получаем

ddWt = I (−I R(I ))= −I 2 R(I ) ≤ 0 .

Следовательно, рассматриваемая электрическая цепь является диссипативной системой, в которой полная энергия переходит в джоулеву теплоту, выделяющуюся при протекании тока через резистор. Это приводит к затуханию колебаний. Если можно пренебречь сопротивлением R резистора, то электрическая система будет соответствовать консервативной системе, так что ММ такой электрической системы может при определенных условиях описывать периодические колебания.

101