5.3. Некоторые нестационарные математические модели

Иногда некоторые нестационарные ММ технических устройств можно привести к нелинейному ОДУ первого порядка

где u(t) — действительная функция действительного аргумента t.

Пусть функция f (t, u) , определенная в области G, удовлетворяет условию Липшица в

G относительно u, т.е. существует такое число L > 0 , называемое постоянной Липшица, что для любых двух точек (t, x) и (t, y) из G выполнено неравенство

f (t, x) − f (t, y) ≤ L x − y .

Пусть функция f (t, u) непрерывна в прямоугольной замкнутой области

D ={(t, u) R2 : t −t0 ≤ a, u −u0 ≤ b} G ,

тогда, согласно теореме Коши, существует единственное решение ОДУ (60) с начальным условием u(t0 ) = u0 . Это решение определено при

t −t0 ≤ h ,

Если выполнены условия теоремы Коши, то решение ОДУ непрерывно зависит от начального условия и правой части ОДУ. Если к тому же правая часть этого ОДУ зависит от некоторого параметра α A R , где A — интервал числовой прямой, то решение задачи Коши

dudt = f (t, u(t), α) , u(t0 , α) = u0

непрерывно зависит от параметра α при дополнительном условии непрерывной дифференцируемости функции f (t, u, α) по α на множестве

D ={(t,u,α) R3 : (t,u) D R2 , α A R}.

Свойство непрерывной зависимости решения важно при рассмотрении многих прикладных задач, поскольку начальное условие, правая часть ОДУ или параметр известны лишь приближенно.

Если имеет место непрерывная зависимость решения от параметра α, то изменение этого параметра не приведет к резкому изменению расположения интегральных кривых на плоскости tOu. Пусть непрерывная зависимость решения задачи Коши от параметра α нарушается, и в окрестности некоторого значения α0 параметра α происходит качественная перестройка расположения интегральных кривых на плоскости tOu. Тогда это явление называют

бифуркацией, а значение α0 — бифуркационным значением.

Выявим особенности интегральной кривой, являющейся графиком решения ОДУ (60), для случая, когда правая часть этого ОДУ не зависит явно от времени, т.е.

dudt = f (u) .

93

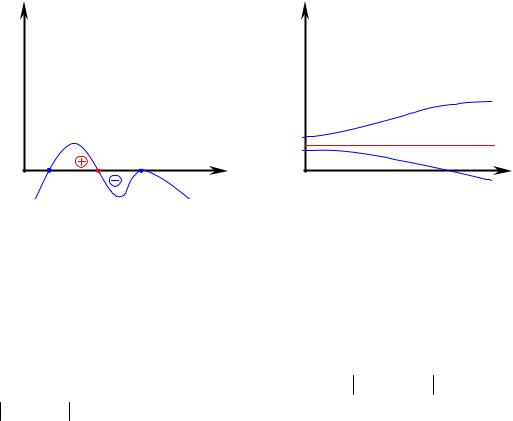
Вид этой кривой зависит от того, имеет или нет уравнение f (u) = 0 действительные корни. Если таких корней нет, то производная функции u(t) знакопостоянна, а функция u(t) строго монотонна (возрастает или убывает).

Пусть уравнение f (u) = 0 имеет n N действительных различных корней u1, u2 , ...un . Тогда каждая из прямых u(t) = ui = const , где 1 ≤ i ≤ n , на плоскости tOu будет соответствовать решению ОДУ при условии, что u(t0 ) = ui .

Предположим, что в рассматриваемой области полностью выполнены условия теоремы Коши. Тогда в силу единственности решения ОДУ через любую точку (t0 , ui ) этой облас-

ти пройдет лишь одна интегральная кривая.

Следовательно, интегральные кривые расположенные в полосе между прямыми u(t) = ui = const , где 1 ≤ i ≤ n , не имеют общих точек с этими прямыми. Поскольку в такой

полосе правая часть ОДУ знакопостоянна, то каждой интегральной кривой в этой полосе соответствует строго монотонная функция u(t), а ограничивающие полосу прямые служат горизонтальными асимптотами графика этой функции.

На рис. 49. показан график функции f(u) и соответствующий ей качественный характер интегральных кривых на плоскости tOu.

u3 u2

u1

Рис. 49. Качественный характер интегральных кривых

Выясним условия устойчивости решения u(t) = ui = const ОДУ первого порядка dudt = f (u)

при t > t0 .

Решение ϕ(t) называют устойчивым в смысле Ляпунова, если для любого сколь угодно малого ε > 0 существует δ(ε) > 0 , что из неравенства u(t0 ) −ϕ(t0 ) < δ(ε) следует нера-

венство u(t) −ϕ(t) < ε при t > t0 . Это означает, что в случае устойчивости решения ϕ(t) достаточно близкие по начальным значениям решения u(t) остаются близкими при t > t0 . Если при этом решения ϕ(t) и u(t) сближаются при возрастании t, т.е.

lim [u(t) −ϕ(t)] = 0 ,

t→+∞

то решение ϕ(t) называют асимптотически устойчивым. Решения, не обладающие свойством устойчивости, называют неустойчивыми.

ким образом, по графику функции f(u) можно определить, какие решения u(t) = ui = const являются устойчивыми, а какие — нет.

94

Пример. Рассмотрим электрическую цепь на рис. 50, которая состоит из последовательно соединенных источника постоянного напряжения, катушки индуктивностью L, резистора сопротивлением R и двух электродов, между которыми при их сближении возникает дуговой разряд (вольтова дуга).

Рис. 50. Электрическая цепь, содержащая электроды

Пусть вид нелинейной характеристики дугового разряда UД(I) известен и определяется напряжением на электродах от силы I тока, протекающего в электрической цепи.

Если считать, что при изменении I соответствующие значения UД устанавливаются мгновенно, то в соответствии со вторым законом Кирхгофа изменение во времени t силы тока в этой цепи описывает нелинейное ОДУ первого порядка

Рис. 51. График функции f(I)

Изменение хотя бы одного из параметров U или R приводит к изменению корней уравнения f (I ) = 0 . Если существует непрерывная зависимость решения рассматриваемого

ОДУ (61) от U и R как от параметров, то такое изменение будет непрерывным и не приведет к резкому изменению в расположении интегральных кривых на плоскости tOI.

Рассмотрим случай, когда правая часть ОДУ (61) зависит от параметра U и в окрестности некоторого его значения происходит качественная перестройка расположения интегральных кривых на плоскости tOI.

Пусть функция

U (I )= R I +UД (I ),

95

Предположим, что значение напряжения источника изменяется столь медленно, что

каждому значению соответствует значение I силы тока в электрической цепи. Тогда при увеличении напряжения источника от 0 до U0 тока в электрической цепи сначала не будет и дуговой разряд между электродами не возникает. При медленном возрастании напряжения

от U0 до U2 сила тока растет от нуля до значения I1 , но затем увеличивается скачком до значения I3 , т.е. между электродами возникает дуговой разряд и ток в дуге довольно значителен.

Если после этого начать уменьшать напряжение источника, то I будет уменьшаться сначала непрерывно до значения I2 , а затем скачком до значения I0 , что означает прекра-

щение горения дугового разряда.

На рис. 53 изобразим графики функции f(I) при фиксированных значениях напряжений источника U1, U* и U2.

f

U = U2 = const

Рис. 53. Графики функции f(I) при фиксированных значениях напряжений источника

96

При движении из точки B к точке C число нулей функции f(I) изменяется, действительно, точки, соответствующие значениям I1 и I2, сливаются в одну, соответствующую зна-

чению I1 , т.е. на плоскости tOI вместо прямых I(t) = I1 и I (t) = I2 образуется одна прямая

I (t) = I1 , которая соответствует неустойчивому решению ОДУ.

При движении из точки B1 к точке A1 число нулей функции f(I) также изменяется. Точки, соответствующие значениям I2 и I3, сливаются в одну, соответствующую значению

I2 . Это означает, что на плоскости tOI вместо прямых I (t) = I2 и I (t) = I3 образуется одна прямая I (t) = I2 , которая соответствует неустойчивому решению ОДУ.

Таким образом, при изменении параметра U в правой части ОДУ (61) изменяется качественный характер расположения интегральных кривых.

Значение параметра U, в окрестности которого происходит качественная перестройка расположения интегральных кривых на плоскости tOI, является бифуркационным. В этом примере бифуркационными являются значения U1 и U2 параметра U, а явление, связанное с качественным изменением расположения интегральных кривых, является бифуркацией.

97