Лекция 02.11.2019

Умозаключение – это некая формула?

Посылки, заключения

A₁ , A_n ╞ В

Умозаключение является правильным, если и только если между посылками и заключением имеется отношение лог следования.

Нет такой строчки, где все посылки истины, а В ложно – конкретно так будет выглядеть в таблице истинности.

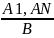
А, А⊃ В, ╞ В

A	A	⊃	B	╞	B
И	И	И	И		И
И	И	Л	Л		Л
Л	Л	И	И		И
Л	Л	И	Л		Л

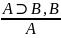
• Если построить таблицу истинности, то получим, что у нас в одной из строчек из истины следует ложь – поэтому такая формула неправильна.

Простая реструктивная дилемма.

⎤A v ⎤B, C ⊃A, C ⊃ B, ⊧⏋C

⏋

A

v

⏋

В

C

⊃

А

C

⊃

В

⊧

⏋

С

Л

И

Л

Л

И

И

И

И

И

И

И

+

Л

И

Л

И

Л

Л

И

Л

И

И

Л

И

И

+

И

Л

Л

И

И

И

Л

И

И

И

И

Л

Л

+

Л

И

Л

И

И

И

Л

Л

И

И

Л

И

Л

+

И

Л

И

Л

И

Л

И

И

Л

Л

И

И

И

+

Л

И

И

Л

И

Л

И

Л

И

Л

Л

И

И

+

И

Л

И

Л

И

И

Л

И

Л

Л

И

Л

Л

+

Л

И

И

Л

И

И

Л

Л

И

Л

Л

И

Л

+

И

Л

ПРАВИЛЬНО

СОКРАЩЕННЫЙ МЕТОД ПОЗВОЛЯЕТ ЗНАЧИТЛЕЬНО СОКРАТИТЬ КОЛ-ВО СТРОК. (на странице 68 в учебнике хорошо написано)

Мы предполагаем, что рассуждение неправильно и решаем, отталкиваясь от этого. Если мы в процессе вычислений впадем в противоречие, то наше рассуждение не верно, а значит, умозаключение верно.

Предположим, что мы не знаем ответа, и что это выражение не правильное.

⏋

A

v

⏋

В

C

⊃

А

C

⊃

В

⊧

⏋

С

И

Л

И

И

Л

И

И

Л

И

И

Л

-

Л

И

Цветом выделила противоречие.

(ну или в зависимости от того, от чего ты будешь плясать у тебя может получится и дизъюнкция не верная - смысл все тот же)

A	⊃	B	A	╞	A
Л	И	И	И	+	Л

Тут нет противоречия - значит, умозаключение не верно.

СПОСОБ ПРОВЕРКИ УМОЗАКЛЮЧЕНИЙ, ИЗЛОЖЕННЫЙ В УЧЕБНИКЕ.

Рассуждение правильно, если тождественна истинна следующая формула:

( A₁ & … & A_N) ⊃ B

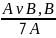
((A v B) & B) ⊃ A

A v B	&	B	⊃	⏋A
И	И	И	Л	Л
И	И	И	И	И
И	Л	Л	И	Л
Л	Л	Л	И	И

ОПРОВЕРЖИМЫЙ, НЕ ЗАКОН – потому что есть противоречие

(натуральный вывод знать не надо, какие-то таблицы знать не надо)