Некоторые, большинство, меньшинство – кванторы существования
Решение сложной задачи:
А ⊃ ⏋B
⏋B ⊃ (C v D) C v ⏋A
⏋D
A v ⏋A – закон лишнего третьего
⏋A ⊃ ⏋A – закон тожества
Сложно конструктивная дилемма нужна теперь
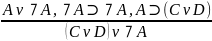
C v ⏋A- - разделительно-категор - все правильно.
Соглашение об опускании скобок.
Скобки играют ту же самую роль, что и запятая. До какой-то степени можно опускать скобки и не попадать в двойственные ситуации. Соглашение
Всегда опускаются внешние скобки
Логические связки ранжируются по степени «силы»
Запишем порядок «притяжения формул к себе»
От сильного к менее сильному –
⏋, &, V, ⊃, ≡
Например,
(p v ( q & ⏋r)) = p v (q & ⏋r) = p v q & ⏋r
Построение таблицы истинности
Конъюнкция истинна – когда обе истины, в других случаях нет. (в общем, см связки – они у нас уже есть).
2n – экспонента (быстрый рост) – количество строк исчисляется (функция перебора)
Где, n – переменная?
Мы будем действовать в пределах 3.
p⊃ p – тут импликация - выполнима, тождественно-истинная
И И И
Л И Л
p ⊃ ⏋ p – выполнима, опровержима
И Л Л И
Л И И Л
P v ⏋q
И И Л И
И И И Л
Л Л Л И
Л И И Л
(P v ⏋q ) ⊃⏋p – выполнима, опровержима
И И Л И Л Л И
И И И Л Л ЛИ
Л Л Л И И И Л
Л И И Л И И Л
1 ЗАДАЧА
Задача на определение видов формулы. Формула называется выполнимой, если её итоговый столбец содержит хотя бы 1 истину.
Формула называется опровержимой, если ее итоговый столбец содержит хотя бы 1 ложь.
Тожественно истинной – если все истинны. Законы логики, которые еще называются тавтологией. В логике тавтология не имеет негативного аспекта.
A v ⏋A
И И Л И
Л И И Л
⏋( A v ⏋A) - опровержимая!!!
Л И И Л И
Л Л И И Л
Пример, p v (q & ⏋r )
И |
И |
И |
Л |
Л |
И |
И |
И |
И |
И |
И |
Л |
И |
И |
Л |
Л |
Л |
И |
И |
И |
Л |
Л |
И |
Л |
Л |
Л |
И |
Л |
Л |
И |
Л |
И |
И |
И |
И |
Л |
Л |
Л |
Л |
Л |
Л |
И |
Л |
Л |
Л |
Л |
И |
Л |
Выполнимая, опровержимая
(не делать таблиц больше 16 строчек)
2 задача
С помощью таблиц истинности можно находить отношения между сложными суждениями.
Л |
И |
Л |
И |
И |
Л |
И |
И |
Л |
И |
Л |
Л |
И |
Л |
Л |
Л |
Л |
И |
И |
Л |
И |
Л |
И |
И |
И |
И |
Л |
Л |
Совместимы по истинности – 2 строчка
Совместимы по ложности – 4 строчка
╡- 1, 3 строчка
╞ - не 1, 3 строчка ---- подчинение
3 задача
p q
И |
|
И |
И |
|
Л |
Л |
|
И |
Л |
|
Л |
Совместимы по истинности – 1 строчка
Совместимы по ложности – 4 строчка
Нет следования – независимость