Отрицание суждений
Мы постоянно что-то отрицаем. Отрицание суждения А – это получение суждения Р, которое находится в противоречии с А.
⎤ А (неверно, что А)
Проблема
перевода внешнего отрицания во внутреннее.
Отрицание простых суждений
Все ли пишут лекцию - ставим отрицание – Не все пишут лекции
Во внутреннем – Все не пишут лекцию.
ТО, ЧТО МЫ ЗАПИСАЛИ – ОШИБКА! Некоторые считают, что общее остается общим, а чатсное остается частым.
Общие
при отрицании переходит в частное и
наоборот – 1 правило
Неверно, что все студенты люди ≡⎤SaP
≡SoP≡ - некоторые студенты, не являются людьми
Неверно, что Москва не является столицей - ⎤s не есть P ≡
Единичные при отрицании остаются единичными - 2 правило.
Москва – столица.
Отрицание реляционных суждений
Неверно, что все студенты (каждый студент) знают какой-то иностранный язык.
Общее
Частное
Утвердительное
Должно стать частно обще отрицательным.
Некоторые студенты не знают ни 1 иностранный языка.
Отрицание сложных суждений
⎤⎤A ≡ A – закон отрицания отрицания
⎤(A&B) ≡(⎤AV⎤B) - отрицания конъюнкции есть дизъюнкция отрицания
⎤ (AVB) ≡(⎤A &⎤B) - ⎤□A ≡ ◇⎤A
⎤ (A⊃B) ≡ (A & ⎤B) - ⎤◇A ≡ □⎤A
⎤ (A≡B) ≡ (AVB)
Самая тяжелая тема – Дедуктивные умозаключения – 19.10.2019
2 самые распространённые темы экзамена:
Таблицы истинности
Силлогизм
Вопросы:
Традиционные умозаключения
Таблицы истинности – все вопросы
Непосредственные умозаключения
Силлогизм
Дедукция – что мы знаем о ней. Метод научного познания – от общего к частному. Дедукция – выведение. Дедуктивное умозаключение зачастую противопоставляется индуктивному умозаключению. Третий способ научного познания – абдукция (от частного к частному).
Дедуктивные умозаключения носят достоверный характер! Недостаток – отсутствие информативности (выводим то, что и так знаем) – Н-р, все студенты, значит, и Маша студентка! (мы и так это знаем).
Традиционные умозаключения:
Их 4 вида. Разберем как таблицу умножения.
Чисто условные (и посылки, и умозаключения являются условными суждениями)
Если из А следует В, а из В следует С Из А следует С
А⊃В, В⊃С А⊃В
А⊃С ⎤В⊃⎤А
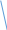
Но такой пример неверный – смотри вниз (Если пошел дождь, то асфальт намек. Если асфальт намок, то пошел дождь – неверно!)
А⊃В А⊃В
В⊃А ⎤А⊃⎤В
Условно
категорические (одна из посылок
условная, другая и заключение –
категорические).
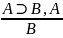
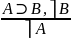
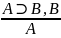
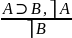
В обычной жизни, мы под «если…то» понимаем «если и только если», поэтому мы говорим, о том, что замена импликации на эквивалентность дадут нам правильные примеры вместо неправильных.
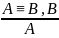
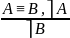
Кул стори от Шангина: поселился рядом сосед, стали знакомиться. Комик спрашивает соседа – чем вы занимаетесь. «Я профессор логики».
-Ого, а что такое логика
- Давайте на примере покажу.
Профессор спрашивает у комика.
- у вас будка есть?
- да есть
- значит, собака у вас есть
- Да, есть собака
- раз у вас есть собака, значит, у вас и семья есть
- да, действительно, все при мне
- ну тогда, вам нравятся женщины
- да, действительно, нравятся женщины
- Вот это и есть логика. Видите, как из факта обладания собачьей конуры я вывел, что вам нравятся женщины.
Комик впечатлен; встретил друга. Поделился новостью.
- что такое логика
- на примере покажу
- (повторяется история с будкой)
- нет будки
- значит, ты женщин не любишь)))
У человека есть конура – А
У человека есть собака – В
…D – любит женщин
А⊃В В⊃C C ⊃D (ход рассуждений)
C⊃D
A⊃D
Покажем, что рассуждение правильное. Вывод получил по транзитивности. Из 3 (см выше).
А вот теперь рассуждения юмориста.
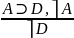
Разделительно категорические – или – (посылка – разделительная (дизъюнкция), посылка и заключение – категорические)
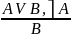
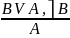
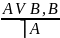
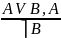
Эти рассуждения становятся правильными, если мы поменяем дизъюнкцию на строгую дизъюнкцию, то рассуждения становятся правильными.
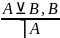
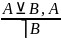
Я поеду в Питер или на автобусе, или на машине. Я поеду на машине. Не поеду на автобусе.
Условно разделительные – (любит спрашивать на экзамене) – они называются так, потому что там есть, и условные, и разделительные, и категорические. С одной стороны, дилеммы делятся на простые (3 суждения) и сложные (4 суждения). С другой стороны, они делятся на конструктивные, деструктивные. В конструктивных – нет отрицания, в деструктивных – появляется.
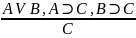(простое) 
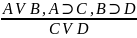(сложное)
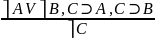
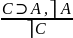
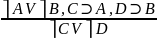– сложная деструктивная дилемма
Таблица истинности
- от нас не будут требовать строить их в обычной жизни, а на экзамене будут…
Это метод, в отличии от контр примера, который всегда работает.
ТАБЛИЧНОЕ ПОСТРОЕНИЕ ЛОГИКИ ВЫСКАЗЫВАНИЯ
Алфавит логики высказывания –
маленькие буквы из середины алфавита. (p, q, r)- пропозиционные переменные
&, V, V, ⊃,≡,⎤ - пропозиционные связки
«Логика при всей свой бесчеловечности, очень гуманитарная наука»- в частности, она будет использовать скобочки – (,) - технические, второстепенные символы (казнить, нельзя помиловать – как ту роль играет запятая – неосознанно поставила запятую в правильном месте ).
Формула – аналог предложения.
Все пропозициональные переменные являются формулами (простые формулы – p, q, r)
Если А и В формулы, то (А & B), (A V B), ( A V B) и т.д. суть формулы
Ни что иное не есть формула
(начнем с опускания скобок)