- •Предмет логики, история логики.
- •2 Лекция – 14.09.2019
- •Лекция 21/09/2019
- •Специфика языка права
- •Тема. Имя
- •Лекция 05.10.2019
- •Отношения между суждениями
- •Отрицание суждений
- •Традиционные умозаключения
- •Непосредственные умозаключения
- •Силлогизм
- •Некоторые, большинство, меньшинство – кванторы существования
- •Построение таблицы истинности
- •Лекция 02.11.2019
- •Непосредственные умозаключения
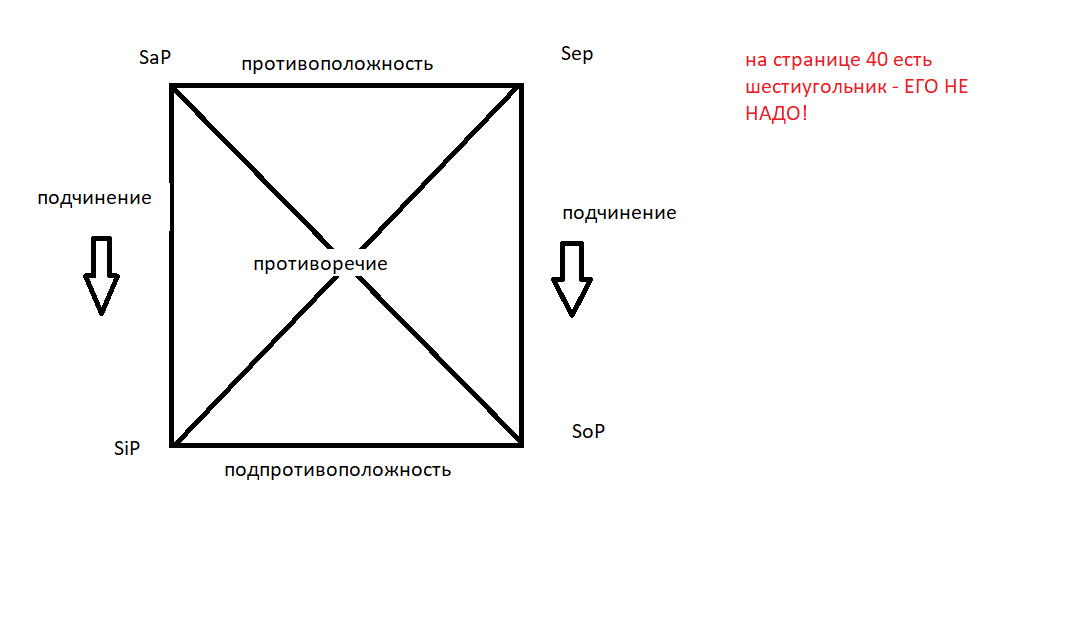
- •Выводы по логическому квадрату
- •Обращение, превращение, противопоставление субъекта и предиката.
- •Простой категорический силлогизм. Энтимема
- •- Состав, фигура и модус силлогизма.
- •Энтимема
- •Логическая и прагматическая характеристика вопросов и ответов
- •Индуктивные умозаключения
- •Понятие абсолютной или безусловной вероятности
- •Тема. Методы установления причинной связи, связанные с явлением исключающая индукция.
- •Метод единственного сходства
- •Метод единого различия
- •Соединенный метод сходства и различия
- •Метод сопутствующих изменений
- •Аналогия (подвопрос индуктивных умозаключение)
- •Понятие
- •Понятие. Обобщение и ограничение понятий
- •Логические основы аргументации – почитать в учебнике эту тему (шире раскрыта)
Лекция 05.10.2019
Второй вопрос прошлой темы – сложные суждения.
- это суждения, в которых можно выделить простые суждения; состоят из простых суждений, соединенных логическими связками.
Виды сложных суждений:
Соединительные – суждения, в которых выражается наличие 2-3 ситуаций. (Конъюнктивные)
Соединительно-конъюнктивное – одновременное наличие 2 ситуаций (как минимум) - &
Последовательно-конъюнктивные
Разделительные – дизъюнктивные
Строго разделительные – V
Нестрого разделит – V
Условные – если-то – импликативные (импликация) виды понимания:
Одна ситуация обуславливает другую ситуацию (причинно-следственная связь) A B
НЕОБХОДИМАЯ ПРИЧИНА – не A не B (Если не полить цветы, они не будут расти; без воздуха, нет человека)
ДОСТАТОЧНАЯ ПРИЧИНА – AB
Суждение логич следования заключают только 1 случай, когда из истины следует ложь
Суждение эквивалентности – равнозначности
Фактическая A <-> B (A B) & (B A)
Логическая A ≡ B (A ⊃B) & (B ⊃A)
Суждение с внешним отрицанием - ⎤- ЛЛИИ – это характеристика (в таких же столбиках) – нет соотношения понятий, оно тут только 1
Модальные суждения – Москва-столица России; а вот утверждение – Необходимо, что Москва – столица России (ложно)
Фактические – то, что не противоречит законом природы
Логические – не противоречит законам логики
Связки (союзы) – и, но, а и так далее – свойство соединять, поэтому соединительные связки (конъюнкция) – &
Или, либо… - разделительное (дизъюнкция) – V
Или- или – строго разделительное - ⊻
Если то, следовательно, потому что, так как – условия, импликация - ⊃
Если и только если - равнозначные, эквивалентные - ≡
Неверное что, ложно что – отрицательное, негативное - ⎤
Связка глагол
Есть, суть – утвердительная
Не суть, не есть – отрицательная
Кванторы – количественные слова
Все, каждый, никто, ни один – кванторы общности
Некоторые, большинство, меньшинство – кванторы существования
Соединительное – примеры
A&B – несколько значений: оба истины, последовательно истинно и ложно или когда оба ложны.
И И И
И Л Л
Л Л И
Л Л Л
И – 1 Л – 0 – обозначение. Желтым отмечено каким будет суждение в целом. Получается истинным будет только в 1 случае, когда обе части истинны.
Разделительные – примеры
A V B
И Л И
И И Л
Л И И
Л Л Л
A V B
И И И
И И Л
Л И И
Л Л Л
Отношения между суждениями
2 вида отношений:
Фундаментальное
Совместимость по истинности – А и В совместимы по истине, если возможна ситуация, когда они одновременно истины
По ложности
Логическое следование (A ⊨B) из А логически следует В, если нет такого случая, когда А истинно, а В ложно (
И Л)
Производное
Противоположные - есть 2, нет 1 – совместимы по ложности, но нет совместимости по истинности
Подпротивоположность0 есть совместимость по истинности, нет совместимости по лжи
Противоречие – нет по истинности, нет по ложности

Подчинение A ⊨B, B
⊨AЭквивалентность A ⊨B, B
⊨AНезависимость – истинность и ложность одного суждения не зависит от истинности и ложности другого A ⊨B, B
⊨A
Противоречащий ни одно и тоже, что и противоположный.
Отношения между простыми атрибутивными суждениями (на 40 странице учебника – но она не полная)
|
(S, P) - равнообъемность |
((S)P) |
((P)S) |
(S ()P) |
((S) (P)) |
(S/P) – противоречие |
|
SaP (есть) |
И |
И |
Л |
Л |
Л |
Л |
|
SeP (не есть) |
Л |
Л |
Л |
Л |
И |
И |
|
SiP (некоторые есть) |
И |
И |
И |
И |
Л |
Л |
|
SoP (некоторые не есть) |
Л |
Л |
И |
И |
И |
И |
|
Только некоторые S есть P
|
Л |
Л |
И |
И |
Л |
Л |
|
PiS |
И |
И |
И |
И |
Л |
Л |
|
Также противоречие Sep и SiP – тоже противоречие.
Sap и SeP не совместимы по истинности, но совместимы по ложности - противоположность.
Всякий раз,
когда SaP истинно, SiP
тоже истинно, но не наоборот – подчинение
SaP ⊨
SiP
SoP и SeP – аналогично с прошлым
SiP SoP – нет эквивалентности.
SoP и SiP не совместимы по ложности, но совместимы по истинности – подпротивоположность