Прагматическая характеристика вопросов и ответов – оценка вопросов и ответов с точки зрения полезности.
Расширительные вопросы. Напр., задавая вопрос в суде, адвокат не должен требовать устранения неопределенности, если это устранение усугубляет виновность подсудимого.
Нерелевантные вопросы – вопросы, не относящиеся к делу. Задача судьи — отклонять такого рода вопросы.
Избыточные ответы – ответы, снижающие не только выраженную в вопросе неопределённость, но и ту, кот. в вопросе не выражена. Напр., подсудимого спрашивают, знает ли он потерпевшего. Подсудимый отвечает, что не знал раньше потерпевшего, но знал его жену.
11. УСЛОВНО КАТЕГОРИЧЕСКИЕ И РАЗДЕЛИТЕЛЬНО-КАТЕГОРИЧЕСКИЕ УМОЗАКЛЮЧЕНИЯ. ДИЛЕММА.
Умозаключение – процесс получения знания, выраженного в суждении, из других знаний, тоже выраженных в суждениях. Посылка умозаключения – исходное суждение. Заключение – получаемое суждение.
Классификация умозаключений:
дедуктивные – связи между посылками и заключениями представляют собой формально-логические законы, в силу чего при истинных посылках заключение истинно;
индуктивные – связи по формам между посылками и заключениями обеспечивают получение только правдоподобного заключения при истинных посылках.
Виды дедуктивных умозаключений:
умозаключения, в которых при осуществлении вывода учитывается внутренняя структура простых суждений;
выводы логики высказываний – умозаключения, в которых при осуществлении вывода внутренняя структура простых суждений не учитывается.
Условно-категорические умозаключения – умозаключения, в которых 1 посылка – условное суждение, а 2-ая посылка совпадает с основанием или следствием условного суждения или же с результатом отрицания основания или следствия условного суждения.
Формы условно-категорических умозаключений:
1. Правильные:
утверждающий модус (если.., то… Если. Следовательно, то.);
отрицающий модус (если.., то… Не то. Следовательно, не если).
2. Неправильные (если.., то… То. Следовательно, если), а также (если.., то… Не если. Следовательно, не то).
Разделительно-категорические умозаключения – умозаключения, в которых 1 из посылок – разделительное суждение, а 2-ая совпадает с одним из членов разделительного суждения или с отрицанием одного из членов этого суждения. Заключение тоже совпадает с одним из членов разделительного суждения или с отрицанием одного из членов этого суждения.
Формы правильных разделительно-категорических умозаключений:
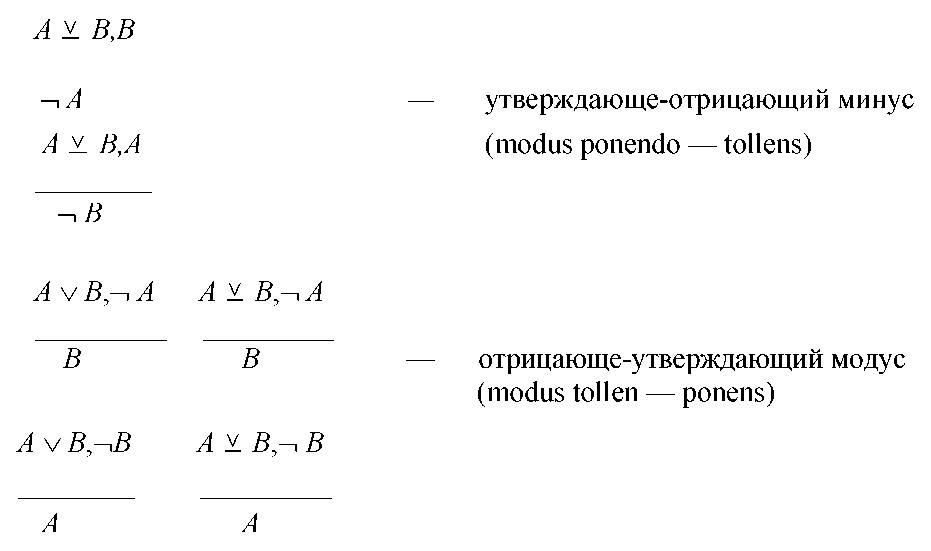
Дилемма – это умозаключение из трех посылок: две посылки — условные суждения, а одна — разделительное суждение. Дилеммы делятся на простые и сложные, конструктивные и деструктивные.
Формы правильных дилемм основных видов указаны в следующей таблице:
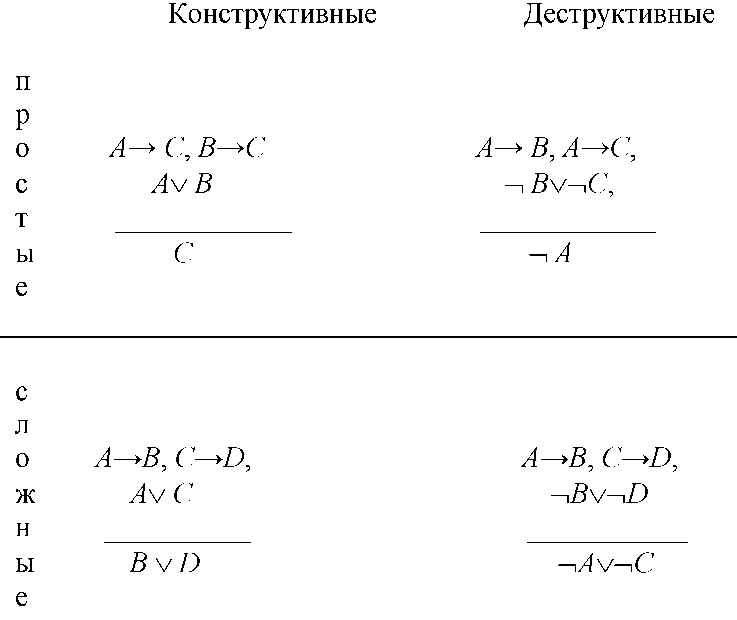
Примером простой конструктивной дилеммы может служить рассуждение Сократа:
Если смерть — переход в небытие, то она благо.
Если смерть — переход в мир иной, то она благо.
Смерть — переход в небытие или в мир иной.
____________________
Смерть — благо.
12. ЯЗЫК ЛОГИКИ ВЫСКАЗЫВАНИЙ. ТАБЛИЧНЫЕ ОПРЕДЕЛЕНИЯ ЛОГИЧЕСКИХ ТЕРМИНОВ.
Табличное построение логики высказываний – один из способов описания выводов логики высказываний. Логика высказываний – раздел символической логики, поэтому в ней используется язык символов.
Символы языка логики высказываний:
p, q, r, s, p1, q1,... — пропозициональные символы (символы для суждений);
¬, &, ∨, →, ↔ — логические термины (константы);
(,) — скобки.
Определение формулы:
Пропозициональная переменная есть формула
Если А - формула и В - формула, то ¬A, (А & В), (A ∨ B), (А ⊃ В), (А ≡ В) — формулы
Ничто иное не есть формула.
Принимаются соглашения об опускании скобок в формулах. Опускаются внешние скобки у отдельно стоящей формулы. Считают, что знак ¬ связывает теснее, чем знаки &, v, ⊃, ≡; знак & — теснее, чем v, ⊃, ≡; знак v — теснее, чем ⊃, ≡; знак ⊃ теснее, чем ≡.
При табличном построении логики высказываний лог. константы определяются посредством таблиц истинности. При этом принимается, что каждое высказывание имеет одно значение — или «истина», или «ложь».
Элементарная формула - формула, являющаяся пропозициональным символом.
Сложная формула - формула, содержащая логические константы. В сложной формуле можно выделить логическую константу, называемую главной логической константой формулы.
Каждую сложную формулу логики высказываний можно единственным образом представить в виде:
¬ А
А & В
A v В
А ⊃ В
А ≡ В
13. СПОСОБ ПОСТРОЕНИЯ ТАБЛИЦ ИСТИННОСТИ ДЛЯ ФОРМУЛ ЛОГИКИ ВЫСКАЗЫВАНИЙ.
Способ построения таблиц истинности для формул логики высказываний:
в таблице под главной константой ф-лы будем писать истинностные значения формулы в целом.
чтобы установить истинностные значения всей формулы, необходимо установить истинностные значения подформул, составляющих ее;
число строк в таблице истинности определяется как 2n+1, где n - число различных пропозициональных переменных, входящих в формулу, а число 2 показывает число истинностных значений;
число столбцов будет определяется как n + О, где n - число логических переменных, а O - количество операций. Количество операций = количество значков;
благодаря тому, что мы разделили сложную формулу на несколько отдельных операций мы можем просто подставить табличные значения для каждой из них;
производим необходимые расчеты и получаем результат.
14. МЕТОД ИССЛЕДОВАНИЯ РАССУЖДЕНИЙ ПОСРЕДСТВОМ ТАБЛИЧНО ПОСТРОЕННОЙ ЛОГИКИ ВЫСКАЗЫВАНИЙ.
Логика высказываний, построенная табличным способом, дает эффективную процедуру для выявления законов логики, а также является методом проверки правильности рассуждений.
Виды формул
Тождественно-истинная (общезначимая) формула (закон логики) - формула, принимающая значение «истина» при любом наборе значений входящих в нее переменных.
Тождественно-ложная формула (противоречие) - формула, принимающая значение «ложь» при любом наборе значений входящих в нее переменных.
Выполнимая (опровержимая) формула – формула, принимающая значение «истина» («ложь») хотя бы при некоторых наборах значений переменных.
Правильное рассуждение – рассуждение, между посылками и заключением которого имеет место отношение логического следования, т.е. если импликация является тождественно-истинной.
Пусть дано какое-то рассуждение. Для определения правильности рассуждения требуется:
обозначить различными символами различные прост. высказывания p, q, r, s
перевести на язык логики высказываний посылки и заключение;
формулы, являющиеся переводом посылок, последовательно соединить знаком конъюнкции;
для полученной формулы построить таблицу истинности.
Если вышло, что что формула тождественно-истинная, то можно сделать вывод о том, что рассуждение правильное. Если тождественно-ложной, то рассуждение неправильное. Если формула является выполнимой и опровержимой, то нет оснований считать рассуждение правильным. Необходимо продолжить анализ рассуждения, но уже ср-вами более богатого раздела логики — средствами логики предикатов.
Если формула содержит много переменных, то в нек. случаях можно не строить таблицу, а путем особых «сокращающих» рассуждений установить, является ли она:
тождественно-истинной
тождественно-ложной
выполнимой и опровержимой.
15. СПОСОБ УСТАНОВЛЕНИЯ ОТНОШЕНИЙ МЕЖДУ СУЖДЕНИЯМИ ПОСРЕДСТВОМ ТАБЛИЧНО ПОСТРОЕННОЙ ЛОГИКИ ВЫСКАЗЫВАНИЙ.
Порядок установления отношений:
суждения переводятся на язык логики высказываний;
для формул, соответствующих суждениям, строятся таблицы истинности;
устанавливаются виды отношений между суждениями.
Основные отношения между суждениями:
совместимы по истинности суждения, когда существует набор значений переменных, при котором формулы принимают значение «И» (то есть существует строка в таблице истинности, в которой эти суждения истинны);
совместимы по ложности суждения, когда существует набор значений переменных, при котором формулы принимают значение «Л»;
логическое следование имеет место между суждениями А и В (АВ), если и только если не существуют суждения А' и В' тех же логических форм, что А' истинно, а В' ложно.
Производные от основных отношения между суждениями:
логическая эквивалентность имеет место между суждениями А и В, если и только если А → В и В → А. Оно обозначается так: А ↔ В. Если они следуют друг из друга;
подчинение имеет место, если и только если А → В и В | А. Знак “|” означает: “не следует”. Суждение А называется в этом случае подчиняющим, а В — подчиненным
контрадикторность (противоречие) имеет место между суждениями, которые не совместимы по истинности и не совместимы по ложности;
контрарность имеет место, если суждения совместимы по ложности, но не совместимы по истинности;
субконтрарность имеет место, если суждения совместимы по истинности, но не совместимы по ложности;
лог. независимость имеет место, если и только если суждения совместимы по истинности и ложности и каждое из них не находится в отношении лог. следования к др. из этих суждений.
16. ВЫВОДЫ ИЗ КАТЕГОРИЧЕСКИХ СУЖДЕНИЙ: УМОЗАКЛЮЧЕНИЯ ПО ЛОГИЧЕСКОМУ КВАДРАТУ, ОБРАЩЕНИЕ И ПРЕВРАЩЕНИЕ.
Выводы из категорических суждений можно подразделить на:
непосредственные умозаключения – выводы из 1 посылки
категорические силлогизмы – выводы из 2 и более посылок
Непосредственными умозаключениями являются превращение и обращение категорических суждений.
Превращение категорического суждения — это изменение его качества одновременно с заменой предиката на противоречащий ему термин. Превращение осуществляется в соответствии со следующими схемами, при этом общеутв. (А), частноутв. (I), общеотриц. (Е), частноотриц. (О).
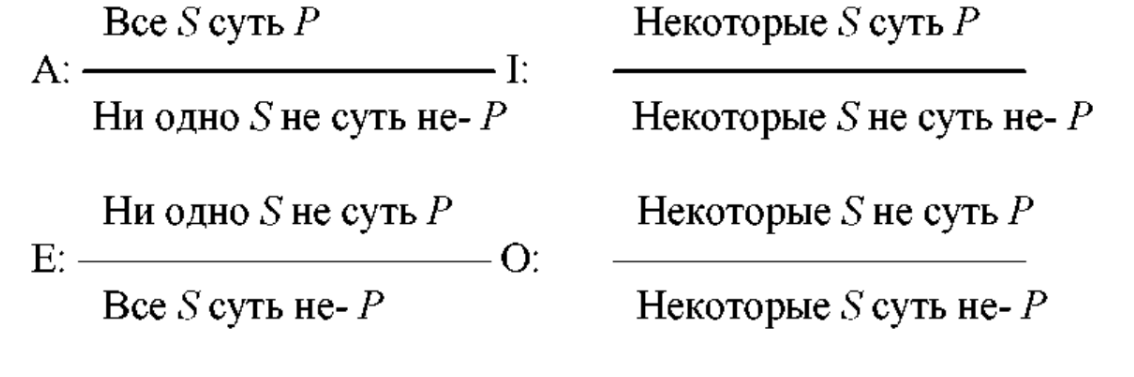
Обращение категорического суждения заключается в перемене местами его субъекта и предиката в соответствии со следующими схемами:
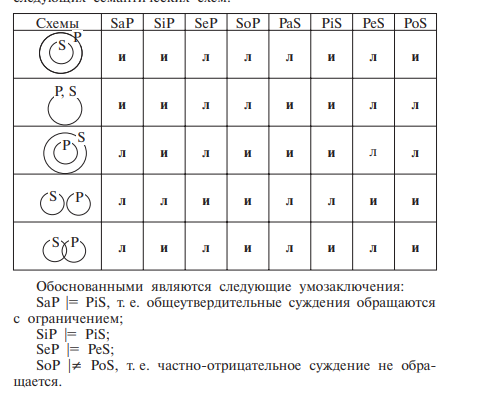
Логический квадрат помогает строить умозаключения, когда известно о истинности или ложности какого-либо одного из категорических суждений одной структуры.
|
Где, SaP – общеутвердительное, SeP – общеотрицательное, SiP – частно-утвердительное, SoP – частно-отрицательное.
|
А+ → Е – , Е+ → А –
А+ → I +, Е+ → О +
I – → А –, О – → Е –
I – → О +, О – → I +
плюс противоречия по диагонали |
Суждения с субъектами, являющимися мнимыми именами, принимаются за бессмысленные. Не обращаются суждения, предикатами которых являются мнимые имена. Если это ограничение игнорировать, то из истинного суждения можно получить ложное. Кроме того, не рассматриваются суждения, в которых объединения объемов субъекта и предиката образуют универсум рассуждения.