3. Способ.

Еще один способ установления отношения логического следования между суждениями, а также и других отношений, заключается в следующем:

• суждения переводятся на язык логики высказываний;

• для формул, соответствующих суждениям, строятся сравнимые таблицы истинности;

• устанавливаются виды отношений между суждениями на основе следующих определений:

1) суждения совместимы по истинности, если и только если в сравнимых таблицах есть строка, в которой все формулы имеют значение “истина”;

2) суждения совместимы по ложности, если и только если в сравнимых таблицах есть строка, в которой все формулы имеют значение “ложь”;

3) из суждений А1, А2, …, An следует суждение В, если и только если в сравнимых таблицах нет строки, в которой все формулы, соответствующие суждениям А1, А2, …, An, имеют значение “истина”, а формула, соответствующая суждению В, имеет значение “ложь”.

Остальные отношения являются производными по отношению к названным. Пример: Пусть переводами трех суждений являются, соответственно, формулы ¬ r ∧ р, p ⊃ q ∨ r, q. Построим для этих формул таблицы истинности таким образом, чтобы эти таблицы можно было сравнивать. Для этого выпишем вначале все переменные, входящие в какие-либо из этих формул. Это переменные р, q, r. Число строк таблиц = 2 = 8. Строим таблицы:

Между первыми двумя суждениями и последним имеет место отношение логического следования. Эти суждения (все три) совместимы по истинности (см. строку 5) и не совместимы по ложности.

УМОЗАКЛЮЧЕНИЯ, В КОТОРЫХ ВЫВОДЫ ОСНОВЫВАЮТСЯ КАК НА СВЯЗЯХ МЕЖДУ ВЫСКАЗЫВАНИЯМИ, ТАК И НА ВНУТРЕННЕЙ СТРУКТУРЕ ПРОСТЫХ ВЫСКАЗЫВАНИЙ

В традиционной логике основными умозаключениями этого типа считали так называемые непосредственные умозаключения и категорический силлогизм.

• Непосредственные умозаключения

1. Непосредственными называются умозаключения из одной посылки, являющейся категорическим суждением (общеутвердительным, общеотрицательным, частноутвердительным или частноотрицательным атрибутивным суждением). Непосредственными умозаключениями являются превращение и обращение категорических суждений. Превращение категорического суждения — это изменение его качества одновременно с заменого предиката на противоречащий ему термин. Превращение осуществляется в соответствии со следующими схемами:

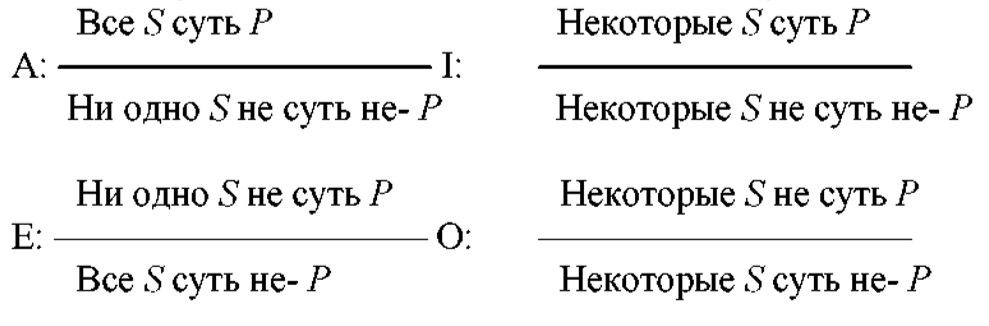
Пример: Некоторые материалисты — метафизики. => Некоторые материалисты не суть не метафизики.

Обращение категорического суждения заключается в перемене местами его субъекта и предиката в соответствии со следующими схемами:

Замечание. Суждения с субъектами, являющимися мнимыми именами, принимаются за бессмысленные. Не обращаются суждения, предикатами которых являются мнимые имена. Если это ограничение игнорировать, то из истинного суждения можно получить ложное. Кроме того, не рассматриваются суждения, в которых объединения объемов субъекта и предиката образуют универсум рассуждения.

Пример: Ни один философ не открыл секрет физического бессмертия (человека). => Ни один человек, открывший секрет физического бессмертия, не является философом. Каждый человек, открывший секрет физического бессмертия, суть не философ. (Результат превращения предшествующего суждения). => Некоторые не философы открыли секрет физического бессмертия (человека).

2. К непосредственным умозаключениям относятся выводы, заключающиеся в превращении категорического суждения и обращении результата превращения (противопоставление предикату), а также в обращении категорического суждения и превращении результата обращения (противопоставление субъекту).

Противопоставление предикату — это умозаключение, в котором субъектом заключения является термин, противоречащий предикату посылки, предикатом — субъект посылки, и заключение и посылка различны по качеству.

Противопоставление субъекту — это умозаключение, в котором субъектом заключения является предикат посылки, предикатом заключения — термин, противоречащий субъекту посылки и заключение и посылка различны по качеству.

Противопоставление предикату и противопоставление субъекту можно осуществлять и анализировать поэтапно (например, в случае противопоставления предикату сначала произвести превращение, а затем осуществить правильное обращение). Общие схемы противопоставления предикату:

... S суть Р=>... не-Р не суть S

... S не суть Р=>...не-Р суть S

Общие схемы противопоставления субъекту:

... S суть Р=> ... Р не суть не-S

... S не суть Р=> ... Р суть не-S

Замечание. Нельзя делать выводы, называемые противопоставлением предикату и противопоставлением субъекту, из суждений с предикатами, являющимися, соответственно, универсальными и мнимыми именами.

Пусть дано умозаключение: Некоторые хозрасчетные предприятия являются рентабельными. => Некоторые нерентабельные предприятия не являются хозрасчетными.

Это умозаключение подпадает под общую схему противопоставления предикату. Чтобы проверить, правильное оно или нет, нужно произвести превращение исходного суждения:

Некоторые хозрасчетные предприятия являются рентабельными => Некоторые хозрасчетные предприятия не являются нерентабельными.

Затем правильно произвести обращение результата превращения:

Некоторые хозрасчетные предприятия не являются нерентабельными. => ?

Частноотрицательное суждение не обращается. Следовательно, приведенное выше умозаключение не является правильным.

Для письменной проверки правильности непосредственных умозаключений можно использовать круговые схемы Эйлера. Пусть дано умозаключение (противопоставление субъекту): Некоторые материалисты (S) — метафизики (Р) => Некоторые метафизики (Р) не суть не материалисты (не-S)

В посылке этого умозаключения утверждается, что некоторые элементы объема имени S входят в объем имени Р. Поскольку слово “некоторые” употребляется в смысле “по крайней мере некоторые, а, может быть, и все”, то в общем случае следует допустить четыре возможности: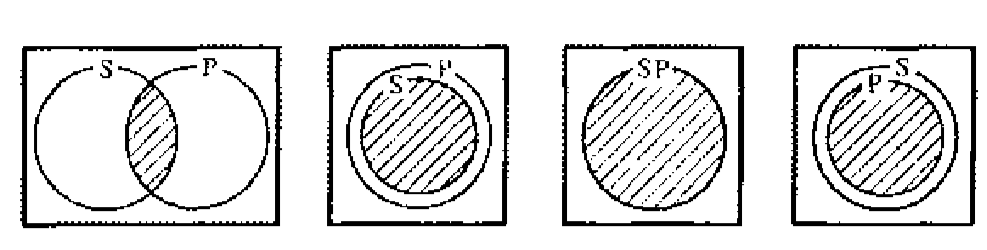

Заштрихованная поверхность соответствует тем элементам объема имени S, которые входят в объем имени Р. Прямоугольником представлен универсум рассуждения — в данном случае, например, класс философов. Что говорится в заключении? Некоторые Р не суть не-S. Во всех ли случаях на приведенных схемах отражено, что (по крайней мере) некоторые элементы объема термина Р не включаются в объем термина не-S? Заштрихуем на схемах горизонтальными линиями поверхности, соответствующие объему термина не-S . Для этого схемы начертим еще раз:

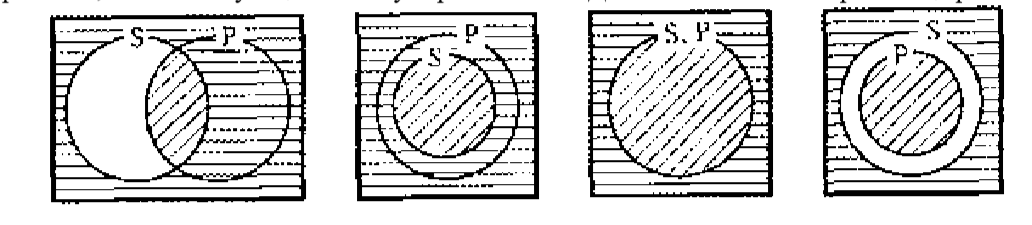
Очевидно, что во всех четырех случаях некоторые Р не являются элементами не-S. Эти элементы объема термина Р представлены поверхностями, заштрихованными наклонными линиями. Анализируемое рассуждение является правильным. Чтобы установить, что непосредственное умозаключение не является правильным, нет необходимости рассматривать все возможные отношения между субъектом и предикатом посылки, при которых она является истинной. Достаточно найти один опровергающий случай.

Рассмотрим схему умозаключения, напоминающего обращение общеутвердительного суждения: Все S суть Р => Все Р суть S

Одной из схем, представляющих возможные отношения между S и Р, при которых посылка истинна, является следующая схема 1.

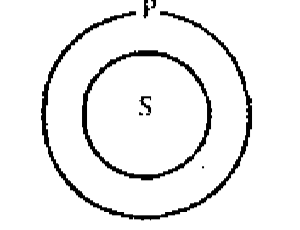
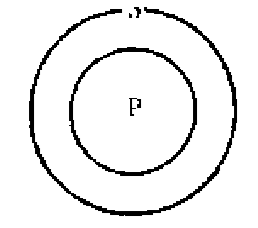
Очевидно, что в этом случае нельзя сделать вывод о том, что все Р суть S, т.е. обращение общеутвердительного суждения без ограничения невозможно (является неправильным). Покажем, что обращение частноотрицательного суждения Некоторые S не суть Р => Некоторые Р не суть S не являются правильным умозаключением. Одной из схем, представляющих возможные отношения между S и Р при истинности частноотрицательного суждения, является схема 2

• Категорический силлогизм

3. Категорическим силлогизмом является умозаключение, в котором из двух атрибутивных суждений выводится третье атрибутивное суждение. В заключении категорического силлогизма связь между терминами устанавливается на основании их отношения к некоторому “третьему” термину в посылках.

Пример: Некоторые поэтические произведения — философские. Все философские произведения — мировоззренческие. => Некоторые мировоззренческие произведения — поэтические.

В категорическом силлогизме три дескриптивных термина, являющихся общими или единичными именами.

1. Термины, входящие в заключение, называются крайними, а термин, входящий в каждую из посылок, но не входящий в заключение, — средним. В примере средним термином является общее имя “философское произведение”. Средний термин обычно обозначается буквой М.

2. Термин, соответствующий субъекту заключения, называется меньшим. Обозначается латинской буквой S.

3. Термин, соответствующий предикату заключения, называется большим и обычно обозначается латинской буквой Р.

Структура приведенного выше силлогизма: Некоторые Р суть М. Все М суть S. => Некоторые S суть Р.

4. Один из способов установления правильности силлогизмов заключается в следующем: нужно проверить, соблюдены ли (общие) правила силлогизмов. Общие правила:

1) по крайней мере одна из посылок должна быть общим суждением;

2) по крайней мере одна из посылок должна быть утвердительной;

3) при одной частной посылке заключение должно быть частным;

4) при одной отрицательной посылке заключение должно быть отрицательным;

5) при обеих утвердительных посылках заключение должно быть утвердительным;

6) средний термин должен быть распределен по крайней мере в одной из посылок;

7) термин, не распределенный в посылке, не должен быть распределен в заключении.

Если все общие правила соблюдены, то силлогизм правильный. Если хотя бы одно из этих правил не соблюдено, то силлогизм неправильный. Факт неправильности силлогизма можно также обнаружить посредством следующего эвристического приема: нужно установить, что какие-то из так называемых правил фигур не соблюдены. (Если правила фигур соблюдены, то это еще не означает, что силлогизм является правильным.)

Фигуры силлогизмов. Фигурами называются типы силлогизмов, выделяемые на основе способов расположения терминов в посылках:

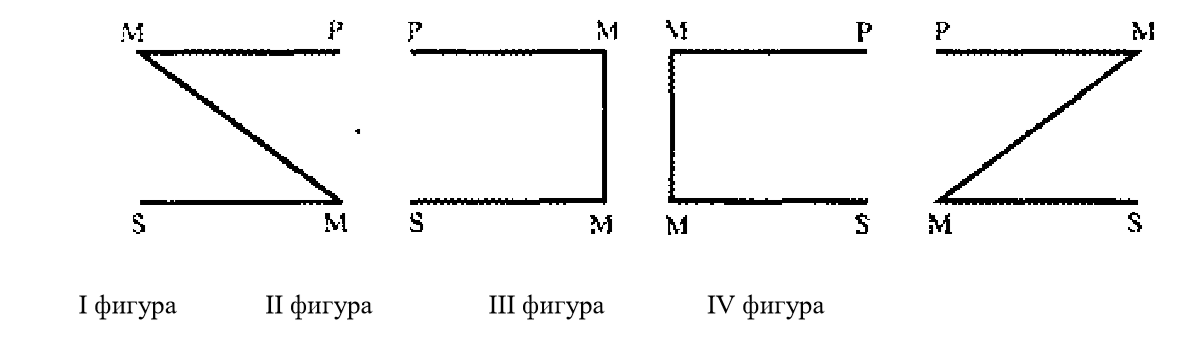
К какой фигуре относится следующий силлогизм? Все металлы — теплопроводные вещества. Все металлы — электропроводные вещества. => Некоторые электропроводные вещества являются теплопроводными.

Сначала нужно выделить меньший и больший термины в заключении. Меньший термин (S) — “электропроводные вещества”, больший термин (P) — “теплопроводные вещества”.

Посылка, в которую входит меньший термин, называется меньшей. Здесь меньшая посылка: “Все металлы — электропроводные вещества”. Посылка, в которую входит больший термин, называется большей. В рассматриваемом примере большей посылкой является суждение: “Все металлы — теплопроводные вещества”. Средний термин (М) — металлы.

Силлогизм относится к третьей фигуре. Его структура:

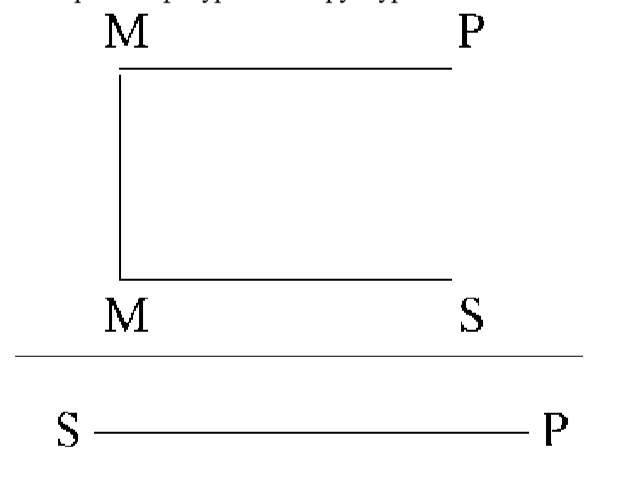
Сформулируем правила трех первых фигур.

Правила I фигуры:

• большая посылка должна быть общим суждением (единичное суждение обычно отождествляется с общим);

• меньшая посылка должна быть утвердительным суждением.

Правила II фигуры:

• большая посылка должна быть общим суждением;

• одна из посылок должна быть отрицательным суждением

Правила III фигуры:

• меньшая посылка должна быть утвердительным суждением;

• заключение должно быть частным суждением.

5. При исследовании силлогизмов также можно использовать круговые схемы. Графический метод заключается в следующем. Выявляются и представляются посредством круговых схем все возможные отношения между терминами одной посылки, затем — второй, при которых посылки истинны. После этого соответствующие схемы совмещаются и проверяется, истинно ли заключение при каждом совмещении выделенных схем. Если да, то силлогизм правильный. Проанализируем таким способом последний из приведенных выше силлогизмов:

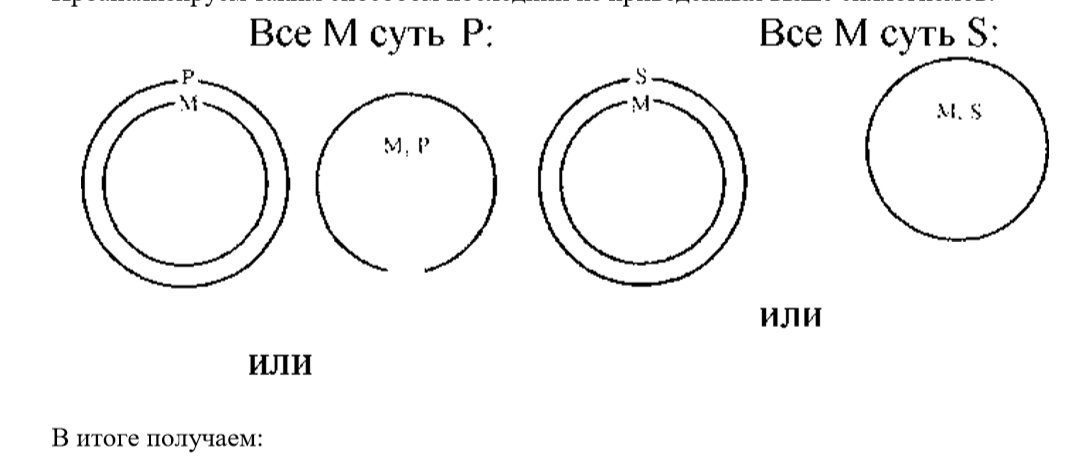
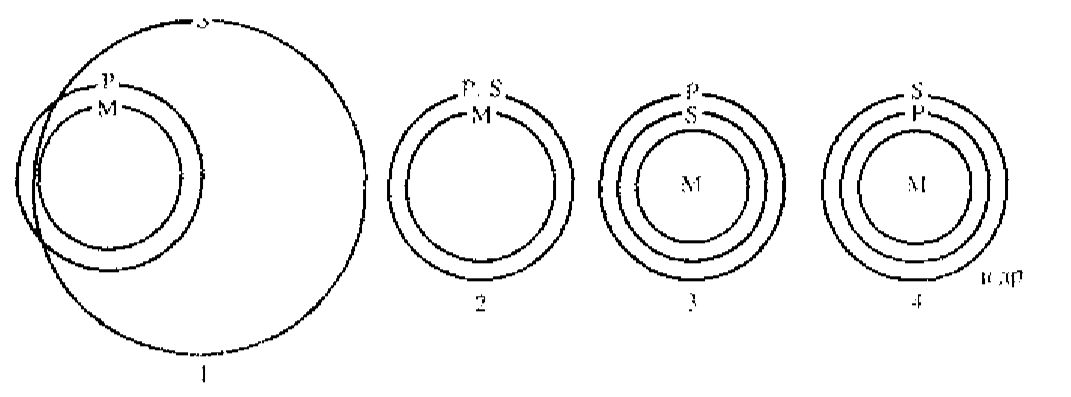Силлогизм неправильный, поскольку в первом и четвертом случаях нельзя утверждать, что все S суть Р. Для установления неправильности силлогизма достаточно обнаружить хотя бы одно отношение между терминами силлогизма, при котором посылки истинны, а заключение ложно.

Рассмотрим силлогизм: Все дельфины — киты. Ни одна рыба не является китом. => Ни одна рыба не является дельфином. Его структура: Все Р сутъ М. Ни один S не суть М. => Ни один S не суть Р.

Возможные отношения между терминами большей посылки, при которых она истинна:

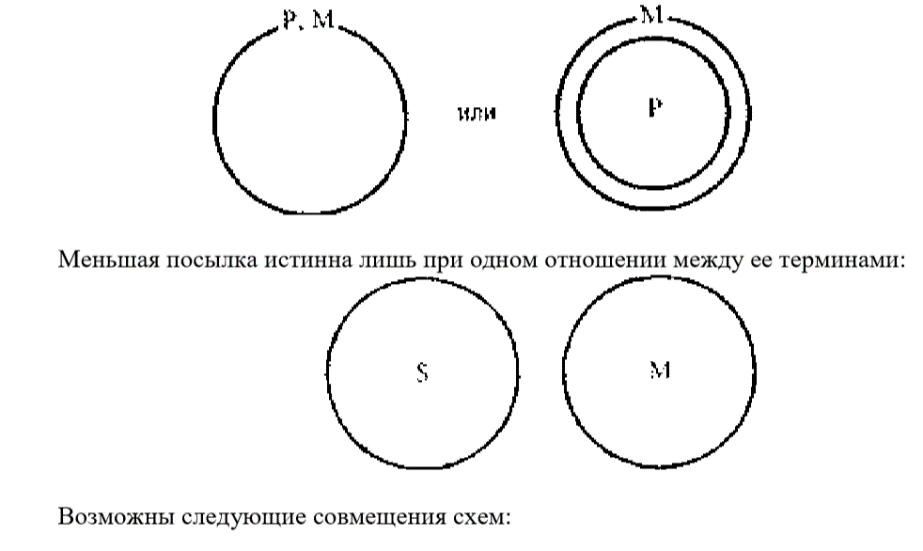
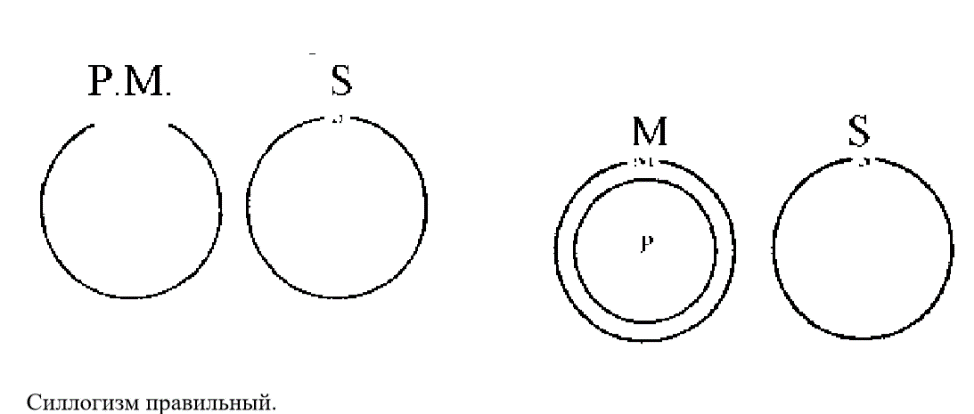
Силлогизмы не всегда высказываются полностью. Часто одна из посылок или заключение опускаются. Такие рассуждения называются энтимемами (от греческого Для проверки правильности энтимемы нужно попытаться восстановить пропущенную часть таким образом, чтобы получился правильный силлогизм. Если этого сделать нельзя, то энтимема является неправильной, если удается, то правильной. При исследовании энтимемы в процессе аргументации целесообразно попытаться установить, является ли восстановленная посылка силлогизма истинной или ложной. Если она оказывается истинной, то аргументация корректная, в противном случае — некорректная.

Пусть дана энтимема, в которой пропущена одна из посылок: Дельфины — не рыбы, так как они киты.

Рекомендуется сначала выделить в энтимеме заключение и написать его под чертой (не высказанное заключение обычно находится легко). Заключение стоит после слов “следовательно”, “поэтому” и соответствующих им по смыслу или же перед словами “так как”, “потому что”, “ибо” и т.д. В приведенном рассуждении заключением является высказывание “Дельфины — не рыбы”. Далее следует выделить в заключении меньший и больший термины и выяснить, какой посылкой является высказывание “Дельфины — киты”. Очевидно, что в это высказывание входит меньший термин, т.е. оно является меньшей посылкой. Имеем: Дельфины (S) суть киты (М).=> Дельфины (S) не суть рыбы (Р).