
ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ
Умозаключение — это процесс получения знания, выраженного в суждении, из других знаний, тоже выраженных в суждениях. Исходные суждения называются посылками умозаключения, а получаемое суждение — заключением. Умозаключения делятся на:
Дедуктивные (от латинского слова “deductio” -“выведение”). В дедуктивных умозаключениях связи между посылками и заключением представляют собой формально-логические законы, в силу чего при истинных посылках (при истинных исходных знаниях) заключение всегда оказывается истинным.
Индуктивные (латинского слова “inductio” - “наведение”). Между посылками и заключением в этих умозаключениях имеют место такие связи по формам, которые обеспечивают получение только правдоподобного заключения при истинных посылках.
Посредством дедуктивных умозаключений “выводят” некоторую мысль из других мыслей, а индуктивные умозаключения лишь “наводят” на мысль.
Различают два вида дедуктивных умозаключений в зависимости от того, учитывается ли в них при осуществлении вывода внутренняя структура простых суждений, входящих в посылки и заключения, или нет.
Умозаключения, в которых при осуществлении вывода внутренняя структура простых суждений не учитывается, они называются выводами логики высказываний. Они делятся на 2 вида:
Условно-категорические. Это умозаключения, в которых одна посылка — условное суждение, а вторая посылка совпадает с основанием или следствием условного суждения или же с результатом отрицания основания или следствия условного суждения.
Пример: Если понятые не приглашены, то процессуальный порядок следственного действия не соблюден. Понятые не приглашены. => Процессуальный порядок следственного действия не соблюден.
Логическая форма этого умозаключения такова: А → В, А, => В. Умозаключения такой формы относятся к утверждающему модусу
А умозаключения формы: А → В, ¬ В => ¬ А — отрицающему модусу.
Умозаключения этих логических форм являются правильными, а умозаключения, например, следующих форм: А→ В, В, =>; А и А → В, ¬ А=> ¬ В — неправильными.
Чтобы выяснить, является ли условно-категорическое умозаключение правильным или нет, нужно выявить его форму и установить, относится оно к одному из правильных модусов или нет. Если оно относится к правильному модусу, то оно правильное. В противном случае — неправильное.
Примеры: Если на хлебоприемном пункте систематически создастся неучтенный резерв зерна, то на нем имеет место хищение зерна. На хлебоприемном пункте имеет место хищение зерна. Следовательно, на хлебоприемном пункте систематически создается неучтенный резерв зерна. Форма этого умозаключения: А→ В, В=> А - умозаключение неправильное.
Если человек умирает, не узнав, что такое любовь, то он уносит с собой в могилу свое горе. Человек умер, не полюбив. => Он унес в могилу свое горе. Форма: А→ В, А=> В - умозаключение правильное.
Разделительно-категорическими. В этих умозаключениях одна из посылок является разделительным суждением, а вторая совпадает с одним из членов разделительного суждения или с отрицанием одного из членов этого суждения.
Заключение тоже совпадает с одним из членов разделительного суждения или с отрицанием одного из членов разделительного суждения. Эти умозаключения тоже будем называть разделительно-категорическими.
Формы
правильных разделительно-категорических
умозаключений:

Примеры умозаключений утверждающе-отрицающего модуса. Это преступление совершено путем действия или же оно совершено путем бездействия. Это преступление совершено путем бездействия. Следовательно, оно не совершено путем действия.
Для установления правильности умозаключения рассматриваемого вида необходимо выяснить, относится ли оно к одному из правильных модусов. Если относится, то оно правильное. В противном случае — неправильное.
В умозаключениях утверждающе-отрицающего модуса в разделительном суждении союз “или” должен быть строго-разделительным. В противном случае умозаключение не будет правильным.
Дилеммы (от греческих слов “ди” — дважды и “лемма” — предположение). Дилемма — это умозаключение из трех посылок: две посылки — условные суждения, а одна — разделительное суждение. Дилеммы делятся на
Простые и сложные
Конструктивные и деструктивные.
Формы
правильных дилемм основных видов указаны
в следующей таблице:

Пример простой конструктивной дилеммы: Если смерть — переход в небытие, то она благо. Если смерть — переход в мир иной, то она благо. Смерть — переход в небытие или в мир иной. => Смерть — благо.
Чисто условные умозаключения. Посылками и заключениями этих умозаключений являются условные суждения.
Контрапозиция. Форму: А→В=> ¬B→¬ A
Пример: Если философ — марксист, то он диалектик => Если философ не диалектик, то и не марксист.
Сложная контрапозиция. Схема: (А∧В) →С => (прерывистое следствие) (А∧¬С) →¬В
Пример: Если Иванов совершил преступление, предусмотренное ст. 156 УК, и он же совершил преступление, предусмотренное ст. 206 УК, то он подлежит наказанию по двум этим статьям. => (прерывистое следствие) Если Иванов совершил преступление, предусмотренное ст. 156 УК, и он не подлежит наказанию по двум статьям — 156 и 206 УК, то он не совершил преступление, предусмотренное ст. 206 УК.
Транзитивность: A→B, B→C => A→C
Импортация: A→ (B→C) => (A∧B) →C
Экспортация: (A∧B) →C, => А→(В→С)
Табличное построение логики высказываний.
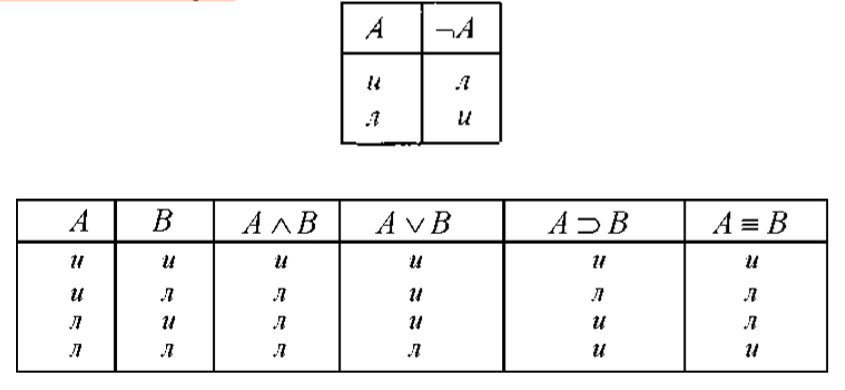
Логика высказываний — раздел символической логики, поэтому в ней используется язык символов. Символы этого языка:
а) p, q, r, s, p1, q1,... — пропозициональные символы (пропозициональные переменные);
б) ¬, ∧, ∨, ⊃, ≡ — логические термины (логические константы);
в) (,) — скобки.
Определение формулы:
а) пропозициональная переменная есть формула;
б) если А есть формула и В есть формула, то ¬A, (А ∧ В),(A ∨ B), (А ⊃ В), (А ≡ В) — формулы;
в) ничто иное не есть формула.
Согласно определению, выражения (р∧q), ((р∧¬q) ≡ (р ⊃ r)), ¬¬ p, r являются формулами, а выражения (p ∨ q) ⊃, r ≡, ∧ (р ⊃ s) — нет.
Примем соглашения об опускании скобок в формулах.
Будем опускать внешние скобки. Условимся считать, что знак ¬ связывает теснее, чем знаки ∧, ∨, ⊃, ≡; знак ∧ — теснее, чем ∨, ⊃, ≡; ∨ — теснее, чем ⊃, ≡; ⊃ теснее, чем ≡. Исходя из сказанного, в формулах ((р∧¬q) ⊃ (r∨s)), (¬¬р ≡ (р ⊃ q)) можно опустить скобки следующим образом: р ∧¬ q ⊃ r ∨ s, ¬¬ р ≡ (р ⊃ q).
При табличном построении логики высказываний логические константы определяются посредством таблиц истинности. При этом принимается, что каждое высказывание имеет одно значение — или “истина”, или “ложь”.
Назовем формулу, являющуюся пропозициональной переменной, элементарной, формулу, содержащую логические константы, — сложной.
В сложной формуле можно выделить логическую константу, называемую главной логической константой формулы. Каждую сложную формулу логики высказываний можно единственным образом представить в виде — ¬ А, или А ∧ В, или A ∨ В, А ⊃ В или А ≡ В. Буквами А и В здесь обозначаются формулы, являющиеся частями сложной формулы. Подформулы, конечно, в свою очередь могут быть сложными формулами. Представив таким образом сложную формулу, мы выделяем в ней последнюю по построению логическую константу, которая и называется главной логической константой формулы. Найдем главную логическую константу формулы ¬ p ∨ q ⊃ p ∧¬ q. Восстановим скобки в этой формуле: ((¬ p ∨ q) ⊃ (р ∧¬ q)). Эту формулу единственным образом можно представить в форме А з В. Ее главным знаком является знак импликации. Можно представить в виде “дерева” процесс построения этой формулы:
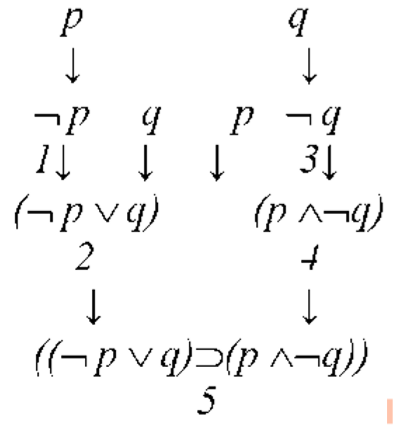
Стрелки показывают, что из формул (или формулы), от которых они направлены, образована формула, к которой они направлены. Цифры под логическими константами указывают порядковый номер константы по построению формулы. Последняя по построению константа имеет номер 5.
Способ.
Построим таблицу истинности для формулы р∨ q ⊃¬ q. В таблице под главной константой формулы будем писать истинностные значения формулы в целом. В этой формуле главной логической константой является знак импликации. Чтобы установить истинностные значения всей формулы, необходимо установить истинностные значения подформул, составляющих ее, т.е. формул р ∨ q и ¬ q. Истинностные значения этих формул будем соответственно писать под логическими константами ∨ и ¬. В результате получим таблицу истинности.

