Лр3 / лр3

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра БТС

ОТЧЕТ

по лабораторной работе №3

по дисциплине «Моделирование биологических процессов и систем» Тема: Моделирование ЭКГ сигнала.

Студент

Преподаватель Тероева Ю. А.

Санкт-Петербург

2022

Цель: изучение модели ЭКГ сигнала на основе генерации эталона в виде суммы несимметричных гауссовых функций.

Основные теоретические положения: в основу построения базовой математической модели генерации искусственной ЭКГ положено аналитическое решение одного из дифференциальных уравнений. Базовая модель формируется по эталону 𝑧(𝑡), который описывается суммой несимметричных гауссовых функций:

г де 𝑡₀ — общая продолжительность (мс) 𝑧(𝑡), связанная с частотой FЧСС сердечных сокращений (уд/мин) соотношением:

а моменты начала 𝑡_i⁽¹⁾ и окончания 𝑡_i⁽²⁾ каждого i -го фрагмента эталона, 𝑖 ∈ {𝑃,𝑄, 𝑅, 𝑆, 𝑆𝑇, 𝑇}, связаны с параметрами 𝑏_i⁽¹⁾, 𝑏_i⁽²⁾ и 𝜇_i следующим образом (поскольку гауссова функция главным образом сосредоточена на «трехсигмовом» интервале, можно полагать так):

Известно, что даже у здоровых людей в состоянии покоя сердечный ритм подвержен значительным колебаниям. Для моделирования этого явления на основе эталона на последовательных временных интервалах:

𝑡_0𝑚 = 𝑡₀ (1 + 𝛾_𝑚), 𝑚 = 1, … , N

ф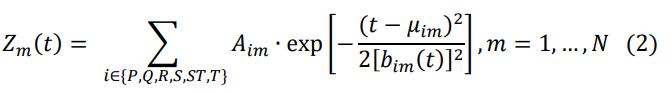 ормируется последовательность циклов Z₁(t)...Z_N(t) по формуле:

i	𝐴𝑖	bi(1)	bi(2)	𝜇𝑖
P	0,11	0,014	0,014	0,399
Q	- 0,004	0,008	0,008	0,45
R	1,453	0,008	0,008	0,474
S	- 1,053	0,007	0,007	0,495
ST	0,063	0,04	0,04	0,574
T	0,52	0,056	0,024	0,7

Таблица 1- Параметры искусственной ЭКГ

Ход работы:

struct WaveParams

    name::String

    A::Float64

    b1::Float64

    b2::Float64

    mu::Float64

end

function model_cmpx(all_waves::Vector{WaveParams},

    t0m::Float64, Fs::Number)

        time_grid = collect(0:1/Fs:t0m) # временная сетка  

        out = fill(0.0,length(time_grid))

        for point in all_waves

     # числитель формулы для Z(t)

            num = (time_grid .- point.mu).^2

    # знаменатель считается в зависимости от mu  

    # так задается ассиметричность волны

            den = Float64[]

            for t in time_grid

                if t<point.mu

                    push!(den, point.b1^2)

                else

                    push!(den, point.b2^2)  

                end

            end        

     # в соответствии с формулой (2) результаты суммируем

            out .+= point.A*exp.(-num./den)

        end

    return out

end

function realECG(all_waves::Vector{WaveParams},

    t0m::Float64, Fs::Number, V::Vector)

        time_grid = collect(0:1/Fs:t0m) # временная сетка  

        out = fill(0.0,length(time_grid))

        for point in all_waves

     # числитель формулы для Z(t)

            num = (time_grid .- point.mu).^2

    # знаменатель считается в зависимости от mu  

    # так задается ассиметричность волны

            den = Float64[]

            for t in time_grid

                if t<point.mu

                    push!(den, point.b1^2)

                else

                    push!(den, point.b2^2)  

                end

            end        

     # в соответствии с формулой (2) результаты суммируем

            A = point.A*(1+rand(V))

            out .+= A*exp.(-num./den)

        end

    return out

end

include("lib.jl")

Fs=500; T=1/Fs;

t0_sec = 1 # базовая длительность комплекса, в сек.

V = collect(-0.2:0.01:0.2) # допуски на вариабельность ритма

N = 20 # число комплексов

all_waves = Vector{WaveParams}()

push!(all_waves, WaveParams("P",0.11,0.014,0.014,0.399))

push!(all_waves, WaveParams("Q",-0.004,0.008,0.008,0.45))

push!(all_waves, WaveParams("R",1.453,0.008,0.008,0.474))

push!(all_waves, WaveParams("S",-1.053,0.007,0.007,0.495))

push!(all_waves, WaveParams("ST",0.063,0.04,0.04,0.574))

push!(all_waves, WaveParams("T",0.52,0.056,0.024,0.7))

ecg = Float64[] # пустой вектор, куда будет собран сигнал

realecg = Float64[]

#ЭКГ только с вариабельностью ритма

for m = 1:N

    t0m = t0_sec*(1+rand(V))

    out = model_cmpx(all_waves, t0m, Fs)

    append!(ecg,out)

end

#ЭКГ с помехами и вариабельностью амплитуды и ритма

for m = 1:N

    Amp = Vector()

for j in 1:6

    push!(Amp, all_waves[j].A)

end

t0m = t0_sec*(1+rand(V))

    out = realECG(all_waves, t0m, Fs, V)

    append!(realecg,out)

end

tmax = T*length(realecg)

x = collect(0+T:T:tmax)

y = Vector()

dreif = Vector()

for i in 1:length(realecg)

push!(y, 0.1*sin(2*pi*50*x[i]))

push!(dreif, 0.3*sin(2*pi*0.25*x[i]))

end

itog = y .+ realecg .+ dreif

#ЭКГ с депрессией ST-сегмента

all_waves_depression = Vector{WaveParams}()

push!(all_waves_depression, WaveParams("P",0.04,0.03,0.03,0.203))

push!(all_waves_depression, WaveParams("Q",0,0.066,0.066,0.266))

push!(all_waves_depression, WaveParams("R",0.64,0.016,0.026,0.296))

push!(all_waves_depression, WaveParams("S",-0.1,0.03,0.03,0.4))

push!(all_waves_depression, WaveParams("ST",-0.23,0.15,0.2,0.45))

push!(all_waves_depression, WaveParams("T",0.06,0.01,0.08,0.7))

ecg_depression = Float64[] # пустой вектор, куда будет собран сигнал

for m = 1:N

    t0m = t0_sec*(1+rand(V))

    out_depression = model_cmpx(all_waves_depression, t0m, Fs)

    append!(ecg_depression,out_depression)

end

using Plots

plotlyjs()

plot(ecg, label="ECG")

plot(x, itog, label="Real ECG", xticks = 0:20, yticks = -1.5:0.3:1.5)

plot(ecg_depression,label="ECG with ST-depression")

Рис 1.Смоделированный сигнал

Рис 2.Смоделированный сигнал приближенный

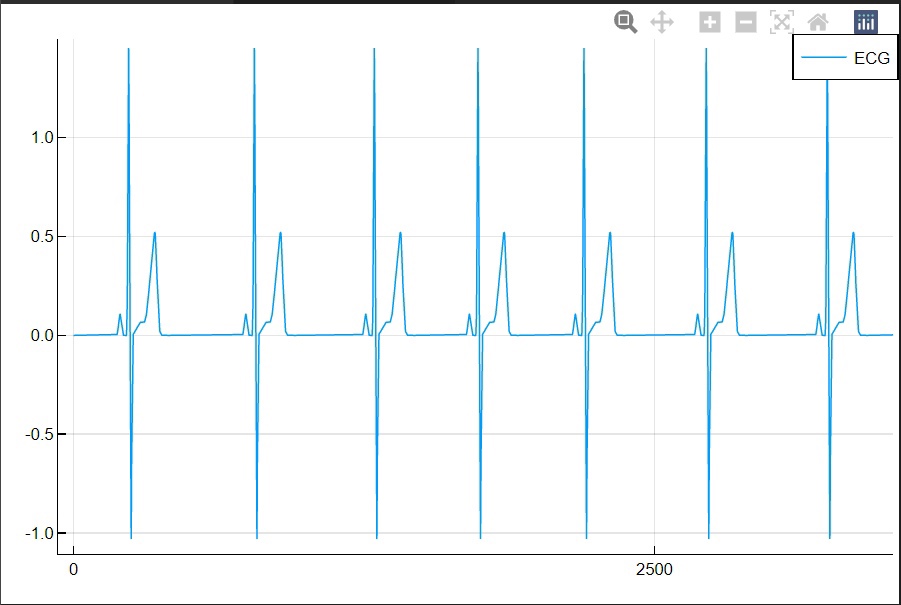
Рис 3.Сигнал ЭКГ с депрессией ST-сегмента

Рис 3.Сигнал ЭКГ с депрессией ST-сегмента приближенный

Рис 4.Сигнал ЭКГ сетевой наводкой и дрейфом

Рис 4.Сигнал ЭКГ сетевой наводкой и дрейфом приближенный

Вывод: в результате лабораторной работы был смоделирован сигнал ЭКГ. Для приближения нашего моделируемого ЭКГ сигнала была добавлена вариабельность значения длительности комплекса (t₀), добавили в модель варьирование по амплитуде зубцов в небольших пределах. Также добавили дрейф изолинии и сетевую наводку в 50 Гц.