Лекции / 12. Библиотеки numpy и matplotlib Jupyter Notebook

In [104]:

y

Out[104]:

array([ 1.1, 3.3, 4.4, 5.5])

Как он работает? Очень просто. (Ну ок, не очень.) Для начала, что такое x < 50 ? Это результат применения операции «сравнение с 50» к каждому элементу массива. То есть это новый массив.

In [105]:

x < 50

Out[105]:

array([ True, False, True, True, True], dtype=bool)

Если в каком-то месте стоит True , то это означает, что на соответствующем месте в x стоит элемент, который удовлетворяет условию, а если False , то не удовлетворяет.

Теперь можно попробовать подставить массив из True и False в качестве индекса в x .

In [106]:

x[ array([True, True, False, False, True]) ]

Out[106]:

Эта штука выбирает ровно те элементы, на чьих местах стоит True — то есть ровно те, для которых выполнялось условие. То, что нам нужно!

А вот так можно проверить несколько условий одновременно:

In [115]:

x[ (x < 50) & (x > 2) ]

Out[115]:

array([ 3.3, 4.4, 5.5])

Скобочки очень важны, иначе ничего не заработает. Операция & соответствует логическому И и опять же выполняется поэлементно.

In [76]:

(x < 50) & (x > 2)

Out[76]:

array([False, False, True, True, True], dtype=bool)

Для логического ИЛИ мы бы исползовали | , а для отрицания ~ .

In [116]:

(x < 50) | (x > 2)

Out[116]:

array([ True, True, True, True, True], dtype=bool)

In [117]:

~ (x < 50)

Out[117]:

array([False, True, False, False, False], dtype=bool)

Результатом такого выбора снова является вид, и это очень удобно, потому что позволяет заменять одни элементы на другие в зависимости от условий и таким образом избавляться от операторов if .

# заменить все элементы, большие 50, на 0

In [122]:

x

Out[122]:

array([ 1.1, 0. , 3.3, 4.4, 5.5])

Кстати, чтобы узнать, правда ли, что два массива равны (в том числе, что состоят из одних и тех же элементов, находящихся в одном и том же порядке), теперь нельзя использовать == — ведь это тоже поэлементная операция!

In [142]:

np.array([1, 2, 3]) == np.array([1, 2, 3])

Out[142]:

array([ True, True, True], dtype=bool)

Чтобы понять, правда ли, что массивы равны, можно использовать такой синтаксис:

In [144]:

(np.array([1, 2, 3]) == np.array([1,2,3])).all()

Out[144]:

True

Здесь мы сначала сравниваем массивы поэлементно, а потом применяем к результату метод all() , возвращающий истину только если все элементы являются истиными. Этот подход часто используется, хотя имеет свои подводные камни (см. на stackoverflow (http://stackoverflow.com/questions/10580676/comparing-two-numpy-arrays-for-equality-element-wise)). Есть и специализированная функция для проверки на равенство:

In [151]:

np.array_equal(np.array([1, 2, 3]), np.array([1, 2, 3]))

Out[151]:

True

Построение графиков в matplotlib

В Python существует много способов строить графики. Мы сейчас рассмотрим самый простой из них, а позже поговорим про более сложные. Для этого нам потребуется библиотека matplotlib , а точнее её часть под названием pyplot . Стандартный способ её импорта выглядит вот так:

In [123]:

import matplotlib.pyplot as plt

Чтобы графики рисовались прямо в ноутбуке, нужно дать вот такую магическую команду:

In [124]:

%matplotlib inline

Простейшее рисование — это функция plot , она принимает на вход список -координат, список -координат и рисует соответствующую картинку либо в виде ломаной:

28.11.2022, 02:19 12 Библиотеки numpy и matplotlib - Jupyter Notebook

In [84]:

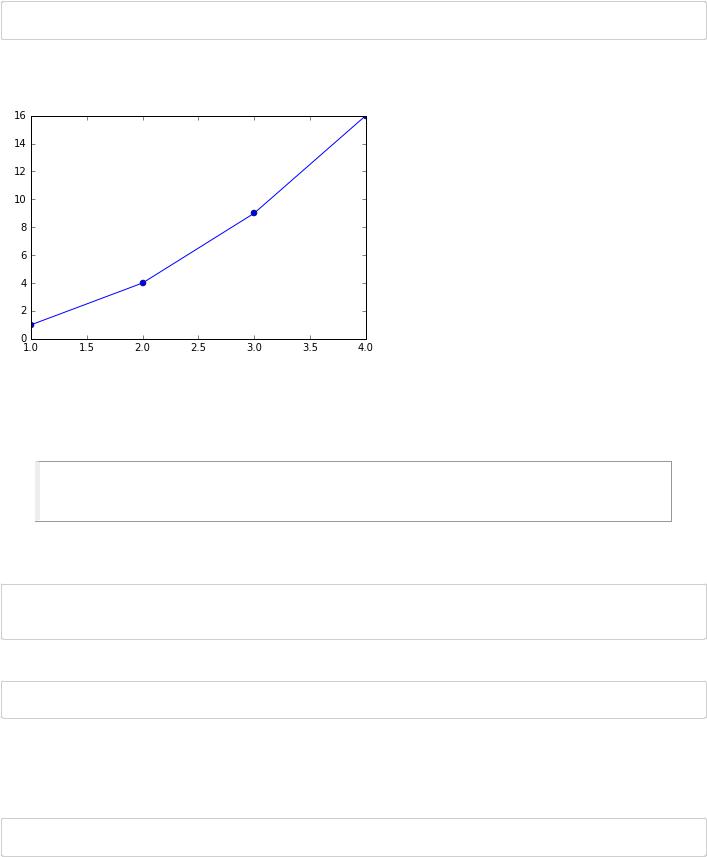
plt.plot([1, 2, 3, 4], [1, 4, 9, 16])

Out[84]:

[<matplotlib.lines.Line2D at 0x10ff2ef60>]

либо в виде отдельный точек:

In [126]:

plt.plot([1, 2, 3, 4], [1, 4, 9, 16], 'o')

Out[126]:

[<matplotlib.lines.Line2D at 0x1112d2550>]

Либо ещё кучей способов.

In [127]:

plt.plot([1, 2, 3, 4], [1, 4, 9, 16], '-o')

Out[127]:

[<matplotlib.lines.Line2D at 0x111394470>]

Посмотрим, как numpy работает в связке с matplotlib.pyplot . Вообще это всё очень похое на MATLAB, и если вы знаете MATLAB, то для вас многое здесь будет знакомо — и наоборот, после numpy и matplotlib.pyplot будете чувствовать себя как дома в MATLAB.

Chewie, we're home. [Здесь должна была быть картинка из «Звёздных войн», но я не могу её включить по соображениям авторских прав.]

In [128]:

x = np.linspace(-5, 5, 200)

# это массив из 200 элементов, состоящий из равномерно разбросанных чисел от -5 до 5

In [129]:

len(x)

Out[129]:

200

In [132]:

x[:10]

Out[132]:

array([-5. , -4.94974874, -4.89949749, -4.84924623, -4.79899497, -4.74874372, -4.69849246, -4.64824121, -4.59798995, -4.54773869])

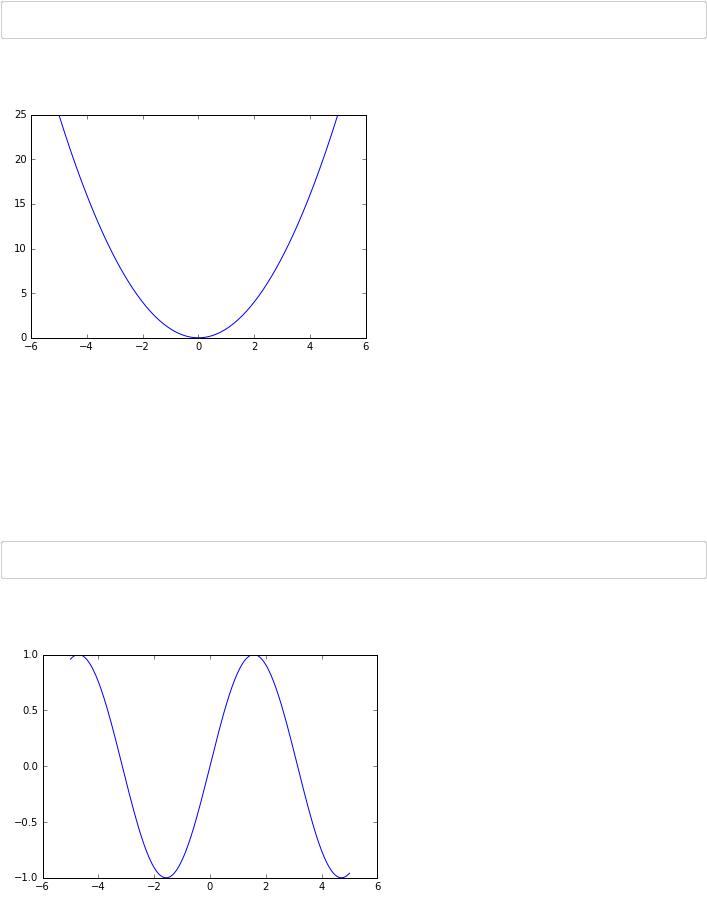
Вот так можно нарисовать параболу:

In [136]:

plt.plot(x, x**2)

Out[136]:

[<matplotlib.lines.Line2D at 0x1115d62b0>]

Действительно, x**2 — это массив, элементами которого являются квадраты чисел, лежащих в x . Значит, построив график, состоящий из точек, -координаты которых записаны в x , а -координаты с x**2 , мы построим график функции .

А вот, например, синусоида:

In [139]:

plt.plot(x, np.sin(x))

Out[139]:

[<matplotlib.lines.Line2D at 0x111758710>]

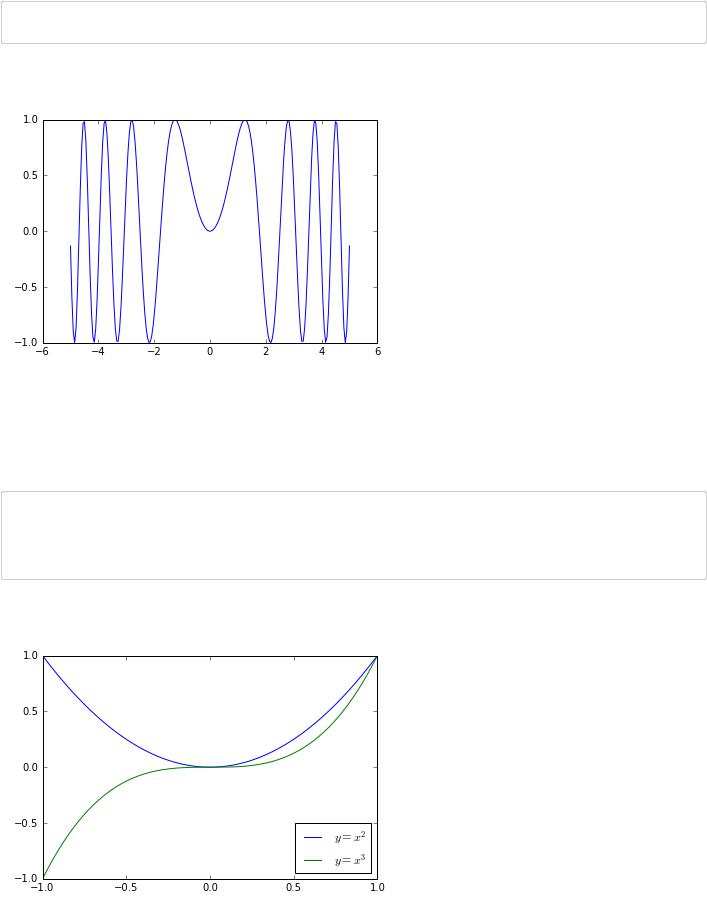
А вот что-то посложнее:

In [140]:

plt.plot(x, np.sin(x**2))

Out[140]:

[<matplotlib.lines.Line2D at 0x11180f7b8>]

Вот так можно построить несколько графиков и сделать подписи.

In [157]:

x = np.linspace(-1,1,201) plt.plot(x,x**2, label = '$y = x^2$') plt.plot(x,x**3, label = '$y = x^3$') plt.legend(loc='best')

Out[157]:

<matplotlib.legend.Legend at 0x111b369b0>

Знак $ в label используется для того, чтобы записывать формулы — это делается в LaTeX (https://en.wikibooks.org/wiki/LaTeX/Mathematics)-нотации и долларами там обозначается начало и конец формулы. (Кстати, в IPython Notebook в ячейках типа Markdown тоже можно записывать формулы в

LaTeX-нотации.)

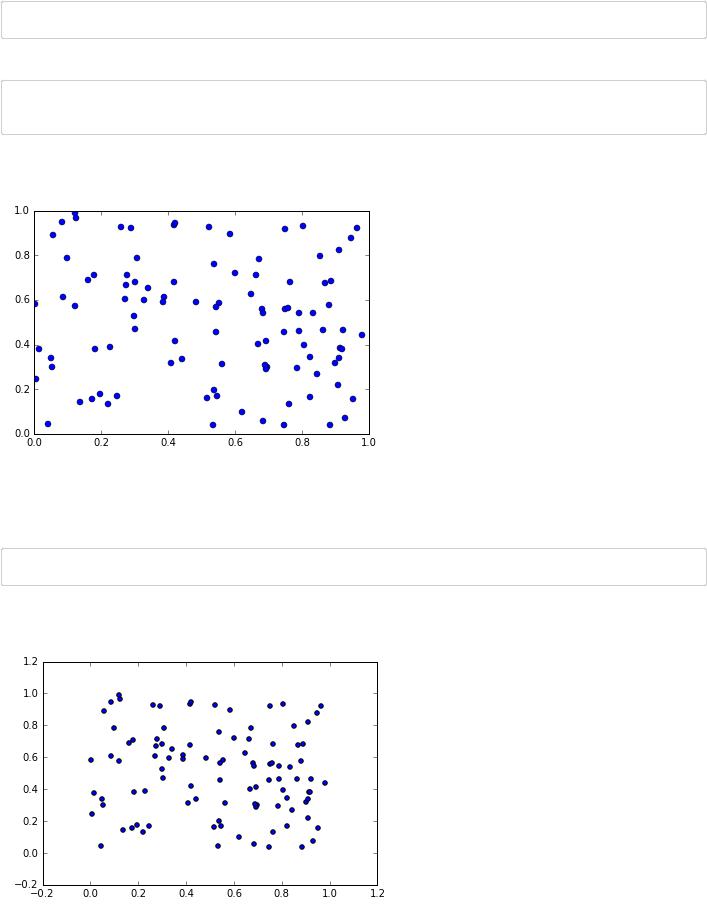
Конечно, мы могли бы получить x и y не в результате вычисления значений какой-то функции, а откуда-то извне. Возьмём для примера случайные числа.

In [152]:

x = np.random.random(100)

In [153]:

y = np.random.random(100) plt.plot(x,y, 'o')

Out[153]:

[<matplotlib.lines.Line2D at 0x1118ee668>]

Есть и специализированная функция для создания scatter plot.

In [154]:

plt.scatter(x,y)

Out[154]:

<matplotlib.collections.PathCollection at 0x1119a8048>

Ещё можно построить гистограмму

(https://ru.wikipedia.org/wiki/%D0%93%D0%B8%D1%81%D1%82%D0%BE%D0%B3%D1%80%D0%B0%D0%B

<a list of 10 Patch objects>)

Можно строить трёхмерные картинки, но тут уже нужна магия и я не буду вдаваться в детали.

In [175]:

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D fig = plt.figure()

<matplotlib.figure.Figure at 0x111b6d668>

In [176]:

%matplotlib inline

28.11.2022, 02:19 12 Библиотеки numpy и matplotlib - Jupyter Notebook

In [178]:

x,y = np.mgrid[-1:1:0.01, -1:1:0.01]

ax = fig.add_subplot(111, projection='3d') ax.plot_surface(x,y,x**2+y**2)

fig Out[178]:

Наконец, можно строить интерактивные картинки!

In [180]:

from ipywidgets import interact, interactive, fixed import ipywidgets as widgets

import numpy as np

import matplotlib.pyplot as plt

In [181]:

%matplotlib inline

In [182]:

def plot_pic(a, b):

x = np.linspace(-3,3,200) plt.plot(x, np.sin(x*a+b))