3.2 Проектирование планетарного редуктора

3.2.1. Исходные данные.

Однорядный планетарный редуктор с внешним зацеплением.

Передаточное отношение планетарного редуктора U=6.136

Число сателлитов k =3

Модуль зубчатых колес m=1

Колеса планетарного редуктора нулевые

Параметры исходного реечного инструмента стандартные

3.2.2. Синтез планетарного механизма.

Дан однорядный редуктор со смешанным зацеплением.

1. 

2. Должно соблюдаться условие соосности, т.е. оси центральных колес при назначенных Z должны совпадать с осью водила. В нашем случае выражение условия соосности имеет вид:

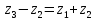
3. Должно выполняться условие соседства (совместности), т.е. должна быть возможность размещения нескольких сателлитов по общей окружности в одной плоскости без соприкосновения друг с другом. Выражение условия имеет вид:

4. Должно соблюдаться условие сборки, т.е. должна обеспечиваться возможность одновременного зацепления всех сателлитов с центральными колесами при равных углах между сателлитами: - целому числу.

5. Должно соблюдаться условие отсутствия подрезания, т.е. при колесах нарезанных стандартным инструментом без смещения (при ;) Z1-4min должно быть больше 18.

Исходя из вышеперечисленных условий находят количество зубьев:

Рассчитают диаметры колес в планетарном редукторе:

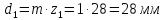
3.2.3. Проверка передаточного отношения графическим способом.

Найдут передаточное отношение графическим способом:

Задали произвольный отрезок АА¢, который изображает линейную скорость точки А. Так как колёса вращаются вокруг оси О, то закон распределения линейных скоростей изобразили линией 1, проходящей через точки О и А¢. Второе колесо имеет в точке А точно такую же скорость. В точке В блок сателлитов имеет скорость, которая изображена отрезком ВВ¢. В точке В водило имеет такую же линейную скорость. Водило вращается вокруг О. Поэтому закон распределения линейных скоростей по водилу изображается линией В, проходящей через точки О и В¢. Углы ψ10 и ψH отложены в разные стороны от вертикали, т.е. входное и выходное звенья вращаются в противоположные стороны.

4. Проектирование кулачкового механизма

4.1. Исходные данные.

Ход толкателя кулачкового механизма выталкивателя
Максимально допустимый угол давления в кулачковом механизме
Соотношение между ускорениями толкателя		-
Угол рабочего профиля кулачка

4.2. Построение кинематических диаграмм движения толкателя с использованием ЭВМ.

По условию задания задан закон изменения аналога углового ускорения толкателя в зависимости от поворота кулачка.

Связь аналогов ускорения и скорости и перемещения толкателя выражается формулами:

В программе MathCAD строим графики передаточных функций ускорения и скорости и функции перемещения от угла поворота кулачка:

4.3. Определение основных размеров кулачкового механизма.

Для определения допустимой области расположения центра вращения кулачка необходимо произвести построение его фазового портрета. Эта операция сводится к построению зависимости передаточной функции скорости толкателя от его перемещения. Затем проведем прямые, касательные к крайним точкам фазового портрета для каждого положения и перпендикулярные аналогам скорости, и отложим от них допустимые углы давления. Проведя под этим углом прямые до их пересечения, получим точку, являющуюся центром кулачка минимальных размеров. Такой кулачок будет обеспечивать прямой и обратный ход толкателя без заклинивания.

Вся область, расположенная под этой точкой и ограниченная двумя прямыми, является областью, каждая точка которой может быть центром вращения кулачка, обеспечивающего прямой ход и реверс без заклинивания. Учитывая то, что мы стремимся спроектировать механизм с наименьшими габаритами, кулачок должен быть минимальных размеров, и, следовательно, центр его вращения должен находиться в точке пересечения прямых.

Данные для построения фазового портрета занесены в таблицу

№поз
0	0	0	0
1	15	0.122	0.016
1’	18.5	0.153	0.025
2	30	0.111	0.051
3	45	0.056	0.073
4	60	0	0.08
5	75	0	0.08
6	90	-0.056	0.073
7	105	-0.111	0.051
8’	116.5	-0.153	0.025
8	120	-0.122	0.016
9	135	0	0

Определены искомые размеры кулачкового механизма:

e₀= 0.003685 м

S₀= 0.029 м

4.4. Построение профиля кулачка.

При графическом построении профиля кулачка применили метод обращенного движения: всем звеньям механизма условно сообщили угловую скорость, равную −w1. При этом кулачок стал неподвижным, а остальные звенья вращались с угловой скоростью, равной по величине, но противоположной по направлению, угловой скорости кулачка.

При построении профиля кулачка с качающимся толкателем из центра O1 проводят в масштабе графика ml окружности радиусами rO и aw. Точку O1 соединяют с произвольно выбранной точкой M0 на окружности радиусом aw . От луча O1M0 в направлении −w1 откладывают угол φраб рабочего профиля кулачка.

Дугу, соответствующую углу φраб делят на части в соответствии с делением оси φ1 на графике SL(φ1). Из точек M0 , M1… M9 проводят дуги радиусом lLM от точек 0, 1…9 на окружности радиусом rO. От точек 0, 1, 2, ... по дугам откладывают в масштабе графика перемещения SL точки L толкателя. Соединяя полученные точки L0 ... L9 плавной кривой, получают центровой профиль кулачка.

В кулачковых механизмах обычно на конце толкателя размещают ролик, главным образом, для уменьшения трения при взаимодействии толкателя и кулачка. Естественно, фактический профиль кулачка с учетом наличия ролика на толкателе будет отличаться от построенного профиля. Чтобы построить фактический профиль кулачка, выбирают радиус Rрол ролика исходя из прочностных или геометрических соображений. для этого часто используют эмпирические формулы:

R_рол= (0.25 – 0.4)r_Oили R_рол< 0,8 ρ_min,

где ρ_min- минимальный радиус кривизны центрового профиля кулачка.

Для получения конструктивного (рабочего) профилия кулачка строят эквидистантный профиль, отстоящий от центрового на расстояние, равное радиусу ролика, который соответствует огибающей к дугам, проведенным из множества точек центрового профиля радиусом ролика.

4.5. Построение графика изменения углов давления.

5. Заключение

В данной курсовой работе были рассчитаны механизмы одноударного холодновысадочного автомата с цельной матрицей.

В результате выполнения работы получены следующие результаты:

1. Определён закон движения звена приведения основного кулисного механизма. Построены диаграммы ω₁=f(φ₁), J_Iпр=95.489 кг · м²;

2. Для заданного положения механизма проведён силовой расчёт, определены реакции в кинематических парах механизма и движущий момент. Величина этого момента, определённая при силовом расчёте, отличается от значения, определённого на первом листе на 4.3%.

3. Cпроектирована эвольвентная цилиндрическая зубчатая передача с числами зубьев Z₁=14 и Z₂=21, коэффициентами смещения x₁=0.6 и x₂=0.5.

4. Спроектирован двухрядный планетарный редуктор с передаточным отношением u_1Н=4.071 и числами зубьев z₁=28, z₂=29, z₃=86.

5. Спроектирован кулачковый механизм по допустимому углу давления. e₀= 0.003685 м, S₀= 0.029 м при допустимом угле давления [υ]=30 град. Радиус ролика толкателя R_p=0.01 м.