3.2 Проектирование планетарного редуктора

3.2.1. Исходные данные.

Двухрядный планетарный редуктор с внешним зацеплением.

Передаточное отношение планетарного редуктора U=-24

Число сателлитов k =3

Модуль зубчатых колес m=1

Колеса планетарного редуктора нулевые

Параметры исходного реечного инструмента стандартные

3.2.2. Синтез планетарного механизма.

Дан планетарный двухрядный редуктор со смешанным зацеплением.

Делят числитель и знаменатель последнего выражения на . В итоге получают:

Проектируемый редуктор должен удовлетворять следующим требованиям:

1. Он должен обеспечивать необходимое передаточное отношение. Для этого записывают выражение, связывающее между собой количество зубьев колес планетарного редуктора (Z₁,Z₂,Z₃,Z₄) и заданное передаточное отношение. В нашем случае выражение имеет вид:

1)

2) Должно соблюдаться условие соосности, т.е. оси центральных колес при назначенных Z должны совпадать с осью водила. В нашем случае выражение условия соосности имеет вид: Z₁+Z₂=Z₄+Z₃

3) Должно выполняться условие соседства (совместности), т.е. должна быть возможность размещения нескольких сателлитов по общей окружности в одной плоскости без соприкосновения друг с другом. Выражение условия соосности имеет вид:

4) Должно соблюдаться условие сборки, т.е. должна обеспечиваться возможность одновременного зацепления всех сателлитов с центральными колесами при равных углах между сателлитами:

- целому числу.

5. Должно соблюдаться условие отсутствия подрезания, т.е. при колесах нарезанных стандартным инструментом без смещения (при ;) Z_1-4min должно быть больше 18.

Исходя из вышеперечисленных условий находят количество зубьев с помощью метода сомножителей. Находим значение выражения .

и раскладываем полученное число на сомножители А, B, C, D, которым числа зубьев Z₁,Z₂,Z₃,Z₄ должны быть соответственно пропорциональны. Чтобы обеспечить соосность механизма вводят дополнительные множители, поставленные в скобки:

С учётом соосности для этой схемы:

Общий сомножитель q подбирают так, чтобы все числа зубьев были целыми и выполнялись условия по количеству зубьев перечисленные в начале этого пункта.

Подбирают А=1, B=5, C=1, D=5, q=4

Тогда

Проверяют выполнения требований:

1. Проверяют передаточное отношение:

2. Проверяют условие соосности:

Z₁+Z₂=Z₄+Z₃

24+120=120+24

3. Проверяют условие соседства:

4. Проверяют условие сборки:

- целому числу.

Верно при

Следовательно, все условия выполняются.

Рассчитают диаметры колес в планетарном редукторе:

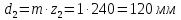
3.2.3. Проверка передаточного отношения графическим способом.

Построим схему механизма в масштабе μ_l=800 мм/м.

Найдут передаточное отношение графическим способом:

Задали произвольный отрезок АА¢, который изображает линейную скорость точки А. Так как колёса вращаются вокруг оси О, то закон распределения линейных скоростей изобразили линией 1, проходящей через точки О и А¢. Второе колесо имеет в точке А точно такую же скорость. В точке В блок сателлитов имеет скорость, которая изображена отрезком ВВ¢. В точке В водило имеет такую же линейную скорость. Водило вращается вокруг О. Поэтому закон распределения линейных скоростей по водилу изображается линией В, проходящей через точки О и В¢. Углы ψ₁₀ и ψ_H отложены в разные стороны от вертикали, т.е. входное и выходное звенья вращаются в противоположные стороны.

Так как ошибка менее допустимой (5%), рассчитанные параметры принимаем.