2.4. Определение реакций в кинематических парах.

Звено 5

Рассмотрим сначала равновесие звена 5:

Реакции F50 и F54 определяем из плана сил для звена 5:

φ₅₀ = 0⁰

φ₅₄ = 248.7⁰

Группа звеньев 4-5

Рассмотрим равновесие группы звеньев 4-5:

Направление реакции F43 и ее значение определяем из плана сил для звеньев 4-5:

φ₄₃ = 248.2⁰

Определяем момент М50:

Группа звеньев 2-3

Рассмотрим равновесие группы звеньев 2-3.

Определяем реакцию F21 из суммы моментов относительно точки D:

φ₂₁ = 113.1⁰

Реакцию F30 определяем из плана сил для звеньев 2-3:

φ₃₀ = 261.2⁰

Звено 2

Рассмотрим равновесие звена 2:

φ₂₃ = 293.1⁰

Звено 1

Рассмотрим равновесие звена 1. Уравнение моментов:

Из уравнения моментов получаем движущий момент, приложенный к кривошипу:

_{Рассмотрим силы, действующие на первое звено:}

Реакцию F10 определяем из плана сил для звена 1:

φ₁₀ = 93.5⁰

2.5. Погрешность нахождения движущего момента на начальном звене.

Неизбежны отклонения в числовых значениях, полученных при выполнении первого и второго листов курсового проекта, которые оценивают относительной погрешностью вычислений (%):

3. Проектирование зубчатой передачи и планетарного механизма

3.1. Проектирование зубчатой передачи.

При проектировании зубчатой передачи существенную роль играет выбор ее геометрических параметров. Геометрический расчет зубчатой передачи производится при условии, что модуль m зубчатых колес получен из расчета зубьев на прочность.

При проектировании зубчатой передачи необходимо выбрать коэффициент смещения стандартного инструмента, который бы обеспечивал допустимую форму зуба, удовлетворял бы ограничению по толщине зуба и, по возможности, обеспечивал одинаковый износ зубчатых колес. Для достижения всех вышеназванных условий, проводится анализ влияния коэффициента смещения инструмента для первого колеса, при заданном коэффициенте смещения инструмента для второго колеса, на различные параметры показателей зубчатого колеса — коэффициентов скольжения колес и коэффициента перекрытия.

3.1.1. Исходный контур инструмента и станочное зацепление.

Стандартом установлены следующие параметры и коэффициенты исходного производящего контура: угол главного профиля  = 20⁰ ; коэффициент высоты головки зуба h^*_а = 1,0; коэффициент высоты ножки h^*_f = 1,25; коэффициент радиального зазора с^* = 0,25; угол наклона линии зуба  = .

При нарезании косозубых колес применяется тот же стандартный инструмент, устанавливаемый наклонно к плоскости заготовки. Принимаем смещение колеса

Параметры определяются следующим образом :

угол профиля

– шаг ,

– модуль зубьев

– коэффициент высоты головки зуба

– коэффициент радиального зазора

Далее расчет ведётся при свободном выборе межосевого расстояния и определяются:

– радиусы делительных окружностей колес

– радиусы основных окружностей

Расчетные коэффициенты смещений идля рассчитываемой зубчатой передачи должны обеспечивать отсутствие подрезания (Х_tmin) и заострения (Х_tmax) зубьев, гарантировать минимально допустимую величину коэффициента перекрытия. Следовательно, должно выполнятся условие Х_tmin<Х< Х_tmax. Для этого определяется наименьшее число зубьев на колесе без смещения, свободное от подрезания

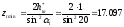
а затем коэффициент наименьшего смещения исходного контура

Максимальный коэффициент смещения не может быть определён.

Его получают путем построения, на графике проводят линию [S_a/m]=0.2, до пересечения с кривой S_a1/m.Точка пересечения и дает значение x₁=x_1max. Отсутствие заострения может быть определено после подсчета толщины зубьев по окружностям вершин; оно отсутствует, если удовлетворено условие:

При выборе коэффициента смещения необходимо учитывать общие рекомендации:

Проектируемая передача не должна заклинивать.

Коэффициент перекрытия должен быть больше допустимого.

Зубья у проектируемой передачи не должны быть подрезаны, и их толщина на окружности вершин должна быть больше допустимой __.

Выбран коэффициент смещения . Он удовлетворяет всем требованиям и соответствует ГОСТ 16532-70.

Угол зацепления передачи определяется по формуле: , где х_=х₁+х₂, а z_=z₁+z₂. При ручном счете угол _tw находится по inv_tw в таблице эвольвентных функций.

_tw=26.3 град

Коэффициент воспринимаемого смещения

Коэффициент уравнительного смещения

Радиусы начальных окружностей

Межосевое расстояние

Исполнительные размеры зубчатых колес:

– радиусы окружностей вершин

– радиусы окружностей впадин

– высота зубьев колес

– толщина зубьев по дугам делительных окружностей

– углы профиля на окружностях вершин зубьев колес

–толщины зубьев по дугам окружностей вершин

Для построения станочного зацепления дополнительно определяются следующие размеры:

– толщина зуба S₀ ИПК по делительной прямой, равная ширине впадины

– шаг

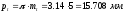
радиус округления