1. Определение закона движения механизма

1.1. Определение размеров механизма.

Проектирование кривошипно-ползунного механизма ведётся по заданным условиям. Требуется определить ход ползуна H, длины звеньев l_DB, l_BC, межосевое расстояние l_OD, положение центра тяжести шатуна l_BS4.

Определяем угол перекрытия по соотношению:

180=36.

Определяем углы начального и конечного положения кривошипа :

Определяем ход ползуна H:

м

Длину l_DB определяем по формуле:

м

Длину шатуна l_BC определяем из соотношения:

м

Определяем межосевое расстояние l_OD:

м

Определяем положение центра тяжести шатуна l_BS4:

м

На листе вычерчивается схема механизма в масштабе:

Вычисления в программе MathСАD приведены в Приложении 1 .

1.2. Нахождение значений передаточных функций.

Для нахождения передаточных функций скоростей и ускорений механизма используем программу MathCAD. Вычисления приведены в Приложении 1.

Кинематические передаточные функции скорости (аналоги скоростей):

Кинематические передаточные функции ускорения (аналоги ускорений):

1.3. Выбор динамической модели механизма.

В качестве звена приведения выбираем кривошип 1. Пользуясь теоремами о равенстве элементарных работ и равенстве элементарных энергий приведём все силы, моменты и массы механизма к динамической модели, чтобы упростить определение закона движения механизма.

1.4. Определение приведенных моментов инерции II-й группы звеньев механизма.

представляет собой сумму приведенных моментов инерции всех звеньев механизма, т.е. , где 1…n – номера подвижных звеньев механизма.

Звенья механизма делят на две группы.

В I группу входят начальное звено и все звенья, связанные с ним постоянным передаточным отношением. Приведенные моменты инерции звеньев I группы – постоянны, их значение не зависит от положения механизма. Их сумма - .

Ко II группе относятся все остальные звенья механизма. Приведенные моменты инерции звеньев этой группы – переменны, они зависят от положения механизма. Их сумма - .

Значения переменных приведенных моментов инерции II группы звеньев вычисляются по формулам:

кгм²

1.5. Определение приведенного момента движущих сил и суммарного приведенного момента.

На механизм действуют моменты от сил тяжести G₄, G₅ звена 4 и силы резания, а также момент от движущей силы.

Сила резания определяется из условия:

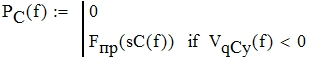
График силы сопротивления приведен в Приложении 1.

Приведённый момент силы сопротивления:

Момент от сил тяжести G₄, G₅ звена 4:

Суммарный приведенный момент силы сопротивления:

Н·м

Механизм работает в установившемся режиме (кинетическая энергия или обобщённая скорость являются периодическими функциями времени). Значит работа сил сопротивления за цикл равна по модулю работе, совершаемой движущими силами.

Работа сил сопротивления за цикл:

Движущий момент найдём по формуле:

Воспользовавшись программой MathCAD, получили, что28.629 Н ·м.

Построим теперь график суммарного момента, сложив момент от движущей силы и момент силы сопротивления :

1.6. Построение диаграммы кинетической энергии для первой группы звеньев.

По методу Н.И. Мерцалова.

График полной кинетической энергии всего механизма получаем по зависимости .

Диаграммы кинетических энергий для первой и второй групп звеньев получают на основании теоремы об изменении кинетической энергии системы:

_График кинетической энергии второй группы звеньев получим из зависимости (Приложение 1). Принимаем, что , так как коэффициент неравномерности вращениямал. Найдем . Так как частота вращения коленчатого вала (определяется в Приложении 1) n₁=0.72 , то

График колебаний кинетической энергии I-ой группы звеньев определяют по уравнению