
Лабораторная работа № 9
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Цель работы — изучение колебательного движения на примере крутильного маятника, определение момента инерции твердого тела методом крутильных колебаний.
О |
1. Метод измерения и расчетные соотношения |
|
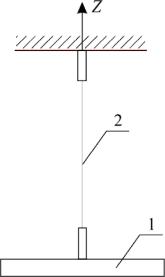
Крутильный маятник (рис. 1) представляет собой твердое тело 1 (диск,
цилиндр, шар, параллелепипед), подвешенное на тонкой упругой прово- |
||||||
локеФ(подвесе) 2 так, чтобы линия подвеса проходила через центр масс |
||||||
тела. При повороте тела относительно оси z на угол в проволоке возни- |
||||||
кает крутящий момент, который стремится вернуть систему в исходное |
||||||
положение равновесия. Если тело отпустить, то оно начнет совершать |
||||||
крутильныеЯколебания. Движение тела можно описать, используя основ- |
||||||
|
С |
|
|
|||
ное уравнение динамики вращательного движения в проекции на ось z |
||||||
|
n |
|
|
|
|
|
I z |
εz M i(z) , |
|
(1) |
|
||
|
i 1 |
Н |
|
|||
|
|
|
|
|
||
где Iz — момент инерции тела относи- |
|
|||||
тельно оси подвеса; z — угловое ускоре- |
|
|||||
|
|
|
n |
|
|
|
ние тела относительно оси z; |
Иi(z) |
|||||
M |
— |
|
||||
|
|
|
i 1 |
У |
||
алгебраическая сумма проекций моментов |
М |
|||||
сил на ось z. |
|
|
|
|
||
Если допустить, что моментом сил |
||||||
|
||||||
сопротивления |
воздуха |
можно прене- |
Э |
|||
бречь, то движение будет определяться |
||||||
|
||||||
только моментом упругих сил, возника- |
И |
|||||
ющих в проволоке при |
ее |
деформации |
||||
кручения. При малых деформациях воз- |
||||||
Рис. 1. Схема крутильного |
||||||
никающий крутящий момент будет про- |
маятника |
|
порционален углу скручивания проволо- |
||
|
ки, равному углу поворота φ тела относительно положения равновесия
Мупр –k . |
(2) |
Знак минус в формуле (2) показывает, что момент упругих сил, воз- |
|
никающих в подвесе, направлен против угла поворота φ, |
препятствует |
выводу системы из положения равновесия и всегда стремится вернуть ее в положение равновесия. Размерный коэффициент пропорциональности k называется модулем кручения.
Модуль кручения — постоянная для данной проволоки величина, определяется как механическими свойствами материала проволоки, так и ее геометрическими размерами.
k G |
πd |
4 |
(3) |
|
32l |
||||
|
|
|||
где G — модуль сдвига (механическая характеристика материала проволоки); d — диаметр проволоки; l — длина проволоки.
С учетом (2), уравнение (1) может быть представлено в виде обык-
новенного дифференциального уравнения второго порядка |
|
||||||||||||||||
О |
|
|
|
I0 d2φ2 kφ |
0 |
|
|
|
|
|
(4) |
||||||
|
или |
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|||
Ф |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
d φ |
2 |
|
|
|
|
|
|
|
||||||||
|
|
и |
|
, |
|
|
|
|
(5) |
||||||||
|
|
dt2 |
ω0φ 0 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
где |
d2φ |
εz |
— угловое ускорение тела относительно оси подвеса; |
|||||||||||||
|
2 |
||||||||||||||||
|
|
k |
|
dЯt |
|
|
|
|
|
|
|
|
|
|
|||
ω0 |
|
— собственная циклическая частота колебаний. |
|
||||||||||||||
|
Iz |
|
|||||||||||||||
|
|
|
С |
|
|
|
|
|
|
|
|
||||||
|
Решением уравнения (5) является функция |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
φ(t) φ0 cosω0t, |
|
|
|
|
(6) |
|||||
|
где |
|
|
|
Н |
|
|
|
|
|
|
|
|||||
|
φ0 — максимальный угол отклонения системы от положения |
||||||||||||||||
равновесия. |
|
|
|
|
И |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Таким образом, колебания системы носят гармонический характер, |
||||||||||||||||
при этом период колебаний определяется выражением |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
У |
|
||||||
|
|
|
|
|
|
|
|
|
|
Т 2π |
2π |
|
Iz |
. |
(7) |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
ω0 |
|
|
|
k |
|
||
|
|
|
|
|
|
|
|
|
|
Методом |
М |
колебаний |
|||||
|
|
|
|
|
|
|
|
|
|
|
крутильных |
||||||
|
|
|
|
|
|
|
|
|
|
можно |
определить момент |
инерции |
|||||
|
|
|
|
|
|
|
|
|
|
твердого тела относительноЭодной из |
|||||||
|
|
|
|
|
|
|
|
|
|
осей, проходящей через его центр масс. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
Из соотношения (7) следует, что, зная |
|||||||
механические свойства материала проволоки и рассчитав модуль кручения k, а также, измерив период колебаний Т, можно найти момент инерции тела относительно оси подвеса.
|
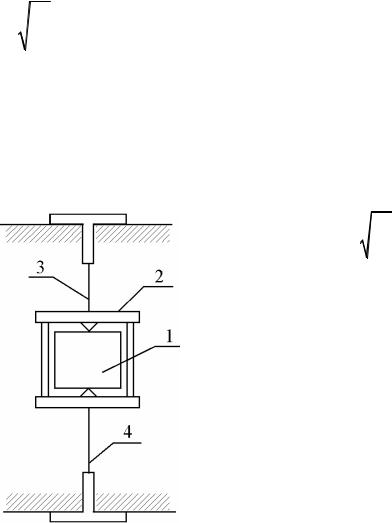
Изучаемое тело 1 (рис. 2) помещается |
|
|
в рамку 2, которая закреплена на двух |
|
Рис. 2. Схема системы подвеса |
вертикальных соосных растяжках 3 и 4, |
|
выполненных из упругих тонких метал- |
||
|
лических проволок-растяжек одинакового диаметра. Наличие двух про- волок-растяжек исключает появление нежелательных дополнительных движений тела, связанных с внешними возмущениями системы.
Длины растяжек в общем случае разные, поэтому при выводе системы из положения равновесия на угол в проволоках возникают свои крутящие моменты
М1 –k1 и М2 –k2 .
Тогда общий крутящий момент, действующий со стороны проволок на систему рамка-тело
Огде k = k1 + k2. |
|
М М1 М2 –k , |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
Учитывая, что |
|
|
|
|
|
|
|
|
|
|
|
|
получаеми |
|
πd 4 |
|
|
|
πd 4 |
|
|||||
k1 G |
|
|
и k2 G |
|
, |
|||||||
32l |
|
32l |
||||||||||
|
|
1 |
|
|
|
|
|
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
||
Яk G |
πd 4 1 |
1 |
|
(8) |
||||||||
|
|
l |
|
|
|
|
||||||
|
32 |
l |
|
|||||||||
|
С |
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как рамка 2 также обладает моментом инерции, то для определения
момента инерции изучаемого тела необходимо провести два опыта. Пусть |
||||||
Н |
|
|
— |
|||
I0 — момент инерции пустой рамки относительно оси подвеса, а Т0 |
||||||
период крутильных колебаний пустой рамки. Пусть также I1 — момент |
||||||
|
|
TИT |
|
|||
инерции системы рамка-тело, а Т1 — период соответствующих колеба- |
||||||
ний. Тогда, используя соотношение (7) можно записать |
|
|||||
|
|
2 |
У |
|
||
|
|
|
2 |
|
|
|
I |
0 |
0 k и |
I |
1 |
k . |
|
|
4π |
1 |
4π |
|
||
|
|
|
|
|||
Поскольку момент инерции системы относительно некоторой оси ра- |
|||||||
|
|
|
|
|
М |
|
|
вен сумме моментов инерции отдельных частей системы относительно |
|||||||
этой оси (свойство аддитивности для момента инерции), то |
|
||||||
|
|
|
I1 I0 Iт , |
|
Э |
(9) |
|
|
|
|
|
|
|||
где |
Iт — момент инерции изучаемого тела. |
И |
|||||
Отсюда |
Iт I1 I0 |
|
|||||
|
|
|
|||||
или |
|
|
|
|
|||
|
|
k |
T12 T02 |
|
|
|
|
|
Iтэ |
|
|
(10) |
|||
|
2 |
|
|||||
|
|
|
4π |
|
|
|
|
где k — рассчитывается по соотношению (8).
Таким образом, экспериментальная задача по определению момента инерции изучаемого тела сводится к измерению периодов колебаний пустой рамки и рамки с закрепленным в ней телом.
Изучаемое тело представляет собой однородный прямоугольный параллелепипед массой m и длинами ребер а, b и c (рис. 4).
Момент инерции такого параллелепипеда относительно оси, перпендикулярной грани со сторонами а и b и проходящей через его центр масс (см. рис. 4, а) рассчитывается по формуле
|
I zт |
m |
a 2 b2 |
(11) |
|
|
|||
|
12 |
|
|
|
Следовательно, можно сравнить экспериментальное значение момента |
||||
инерции тела с его теоретическим значением относительно оси подвеса. |
||||
О |
2. Описание схемы установки |
|
||
|
|
|||
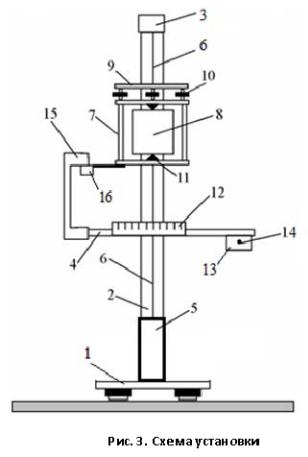
Установка (рис. 3) представляет собой жестко связанную с массивным основанием 1 вертикальную стойку 2, на которой крепятся верхний 3,
жний |
|
|
среднийФ4 |
|
5 кронштейны. Между кронштейнами 3 и 5 на тон- |
ких проволоках-растяжках 6 закреплена рамка 7. Исследуемое тело 8 |
||
Я |
||
|
С |
|
|
|
Н |
|
|
И |
|
|
У |
|
|
М |
|
|
Э |
|
|
И |
фиксируется внутри рамки с помощью прижимной планки 9, зажимных гаек 10 и запорного винта 11. На среднем кронштейне 4 размещена шкала 12 и электромагнит 13, фиксирующий рамку при заданном начальном угле поворота системы относительно положения равновесия. Фиксация рамки в начальном положении производится включением тумблера 14.
3. Порядок выполнения работы
1. Заполните табл.1 спецификации измерительных приборов. Запишите данные установки, которые приведены на лицевой панели. Запуск установки и измерение периода колебаний можно производить в «ручном» режиме, используя секундомер с ценой деления 0,2 с.
В зависимости от конструкции установки возможно использование автоматической системы запуска и измерения времени электронными средствами, в состав которой входят инфракрасный датчик перемещения и электронный секундомер, позволяющий производить отсчет времени заданного числа периодов N.
2. С помощью штангенциркуля измерьте длины ребер исследуемого |
|||||||||||||||||
О |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
параллелепипеда а, b и c. Измерения длины каждого ребра повторите три |
|||||||||||||||||
раза, меняя место измерения длины ребра. Результаты запишите в табл.2. |
|||||||||||||||||
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
|||
|
Спецификация измерительных приборов |
|
|
|
|||||||||||||
|
Я |
|
|
|
|
|
|
Инструментальная |
|
|
|||||||
|
Название |
Пределы |
|
Цена |
|
|
|
|
|||||||||
|
прибораСи измерения |
деления |
|
|
|
погрешность |
|
|
|||||||||
|
его тип |
Н |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Данные установки: |
|
|
|
|
|
|
|
|||||||
Масса параллелепипеда |
|
|
|
У |
,Δm = . |
|
|
||||||||||
|
|
|
m = |
|
|
|
|
||||||||||
Модуль сдвига материала нити |
G = , |
|
,ΔG = . |
|
|
||||||||||||
Диаметр нити |
|
|
|
|
|
d = |
|
|
,Δd = |
|
|
||||||
Длина нити над грузом |
|
|
|
М |
. |
|
|||||||||||
|
|
|
l1 = |
|
|
,Δl1 |
= |
|
|||||||||
Длина нити под грузом |
|
|
|
l2 = |
|
|
,Δl2 |
= . |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Э |
||||
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
|
|
|
|||
|
Результаты измерений длины ребер параллелепипеда |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||
|
|
|
№ |
|
a, мм |
|
b, мм |
|
c, мм |
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Среднее |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
Таблица 3 |
|
|
Результаты измерений времени десяти колебаний |
||||||||
|
|
|
крутильного маятника |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
№ |
Ребра |
Ребра |
|
Ребра |
Пустая |
||
|
|
|
a – c |
a – b |
|
b – c |
рамка |
|
|
|
|
|
τ1, с |
τ2, с |
|
τ3, с |
τ0, с |
|
|
О |
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
Среднее |
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
3. Закреп те исследуемый параллелепипед в рамке так, чтобы ребра |
|||||||||
а и b наход л сь в плоскости, перпендикулярной оси вращения, а ось |
|||||||||
вращения проход ла через центр масс. |
|
|
|
||||||
4. Измерьтеивремя 1 |
десяти полных колебаний системы. Измерения |
||||||||
повторите 3 раза. Результаты измерений занесите в табл. 3. |
|||||||||
5. ЗакрепитеЯпараллелепипед в рамке так, чтобы ребра а и c находи- |
|||||||||
лись в плоскости, перпендикулярной оси вращения, а ось вращения про- |
|||||||||
ходила через центрСмасс. Проделайте три опыта по измерению времени 2 |
|||||||||
|
|
|
Н |
|
|
|
|||
десяти полных колебаний параллелепипеда. |
|
|
|||||||
6. Закрепите параллелепипед в рамке так, чтобы ребра b и с находи- |
|||||||||
лись в плоскости, перпендикулярной оси вращения, а ось вращения про- |
|||||||||
|
|
|
И |
|
|
||||
ходила через центр масс. Проведите три опыта по измерению времени 2 |
|||||||||
десяти полных колебаний системы. |
У |
||||||||
7. Снимите параллелепипед с рамки. Измерьте время 0 десяти полных колебаний пустой рамки. Проделайте опыт 3 раза. Результаты измерений пп. 4—7 занесите в табл. 3.
4.Обработка результатов измерений
1.Проведите статистическую обработку результатов прямых измерений. Вычислите средние значения τ1,τ2,τ3 и τ0 и их абсолютные по-ЭМ
грешности. Рассчитайте периоды колебаний по формуле Т |
|
τi |
. |
|
|||
|
iИ10 |
||
2.Используя данные установки, по формуле (8), рассчитайте эффективное значение модуля кручения системы k.
3.По формуле (10) рассчитайте экспериментальные значения момента инерции параллелепипеда при различных его положениях относительно оси Z (см. рис.4, а, б).
4.По формуле (11) рассчитайте теоретические значения момента инерции параллелепипеда для тех же его положений относительно оси Z ,
что и в п. 3.
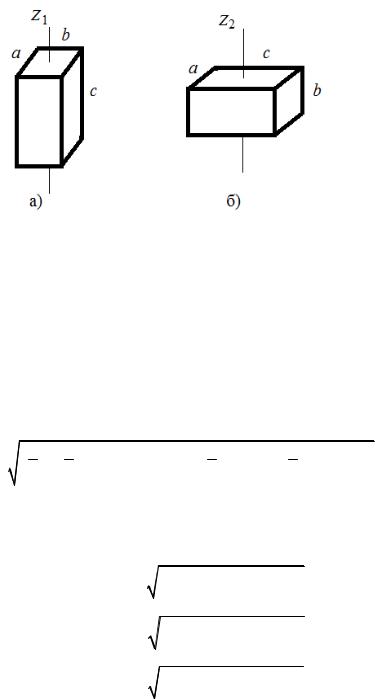
Рис. 4. Схемы расположения прямоугольнго параллелепипеда относительно оси |
||||||||||||||||||||||||||||
О |
|
|
|
|
|
|
|
|
|
|
|
вращения |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Примечан е. |
|
Для положения параллепипеда относительно оси Z1 |
||||||||||||||||||||||||||
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
a 2 b 2 |
|
, |
|
а для |
рис. 4,б, |
||||||||
изображенного |
|
на |
|
рис. 4, а, |
I |
|
|
|
|
|
|
|||||||||||||||||
|
|
mи |
|
|
|
|
|
|
z1т |
|
12 |
|
|
|
|
|
|
|
|
|
|
|||||||
I z2т |
|
|
a |
2 c 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5. Рассчитайте абсолютную погрешность экспериментальнго значе- |
||||||||||||||||||||||||||||
ния момента инерции параллелепипеда при различных его положениях |
||||||||||||||||||||||||||||
относительно осиСZ по формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
IЭаb |
|
|
1 |
|
|
|
τ |
2 |
τ |
02 2 k 2 |
4k2 |
τ |
2 |
τ 2 |
τ |
02 τ0 2 |
||||||||||||
|
|
2 |
|
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
4π |
N |
|
|
|
Н |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
7. Рассчитайте |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
погрешность |
Iт теоретического |
значения |
момента |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
||||||||
инерции, выбрав соответствующую формулу: |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Iт1 m a2 |
a |
2 |
b2 b 2, |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
У |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Iт2 m |
a2 a 2 c2 c 2, |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
М |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Iт3 |
b2 b |
2 |
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
c2 Эc . |
|||||||||||
5.Контрольные вопросы И
1.Опишите содержание метода крутильных колебаний для измерения момента инерции твердого тела. Какие измерения необходимо выполнить в работе?
2.Являются ли крутильные колебания твердого тела гармоническими колебаниями? Ответ обоснуйте.
3.Дайте определение момента инерции тела относительно оси.
4.Почему при изменении оси вращения исследуемого параллелепипеда меняется период его крутильных колебаний?дартной -
5. |
Каким образом в работе учитывается момент инерции рамки, в ко- |
|
торой закрепляется параллелепипед? |
||
6. |
От каких характеристик зависит момент инерции твердого тела? |
|
7. |
Выполните вывод формулы для экспериментального определения |
|
момента инерции твердого тела методом крутильных колебаний. |
||
8. |
Назовите источники погрешности при определении момента инер- |
|
ции твердого тела методом крутильных колебаний. |
||
9. |
Выведете формулу для расчета погрешности экспериментального |
|
значения момента инерции изучаемого тела. |
||
О |
Рекомендуемая литература |
|
|
|
|
10.Савельев И.В. Курс общей физики: Учебное пособие. В 3-х тт. Т.1. Механика. Молекулярная физика. 5-е изд., стер. — СПб.: Изд-во «Лань». 2006 г. С. 134 — 144; 190 — 195.
11.Д.А. Иванов, И.В. Иванова, А.Н. Седов, А.В. Славов. Механика. Молекулярная ф зика и термодинамика: Конспект лекций/ Под ред. А.В.ЯФ
Кириченко. — М.: Издательство МЭИ. 2003. С.52 — 58, 66 — 73. С Н И У М Э И
