§4.8. Линейная зависимость строк и столбцов матрицы.

Заметим, что строки и столбцы матрицы можно рассматривать как арифметические векторы размеров m и n, соответственно. Таким образом, матрицу размеров можно интерпретировать как совокупностьm n-мерных илиn m-мерных арифметических векторов. По аналогии с геометрическими векторами введем понятия линейной зависимости и линейной независимости строк и столбцов матрицы.

4.8.1. Определение. Строка называетсялинейной комбинацией строк с коэффициентами, если для всех элементов этой строки справедливо равенство:

,.

4.8.2. Определение.

Строкиназываютсялинейно зависимыми, если существует их нетривиальная линейная комбинация, равная нулевой строке, т.е. существуют такие не все равные нулю числа

, .

4.8.3. Определение.

Строкиназываютсялинейно независимыми, если только их тривиальная линейная комбинация равна нулевой строке, т.е.

,

4.8.4. Теорема. (Критерий линейной зависимости строк матрицы)

Для того, чтобы строки были линейно зависимыми, необходимо и достаточно, чтобы хотя бы одна из них была линейной комбинацией остальных.

Доказательство:

Необходимость. Пусть строки линейно зависимы, тогда существует их нетривиальная линейная комбинация, равная нулевой строке:

.

Без ограничения общности предположим, что первый из коэффициентов линейной комбинации отличен от нуля (в противном случае можно перенумеровать строки). Разделив это соотношение на , получим

,

то есть первая строка является линейной комбинацией остальных.

Достаточность. Пусть одна из строк, например, , является линейной комбинацией остальных, тогда

то есть существует нетривиальная линейная комбинация строк , равная нулевой строке:

а значит, строки линейно зависимы, что и требовалось доказать.

Замечание.

Аналогичные определения и утверждения могут быть сформулированы и для столбцов матрицы.

§4.9. Ранг матрицы.

4.9.1. Определение. Минором порядка матрицы размераназывается определитель порядка с элементами, расположенными на пересечении некоторых ее строк и столбцов.

4.9.2. Определение. Отличный от нуля минор порядка матрицы размераназываетсябазисным минором, если все миноры матрицы порядка равны нулю.

Замечание. Матрица может иметь несколько базисных миноров. Очевидно, что все они будут одного порядка. Также возможен случай, когда у матрицы размераминор порядка отличен от нуля, а миноров порядка не существует, то есть .

4.9.3. Определение. Строки (столбцы), образующие базисный минор, называются базисными строками (столбцами).

4.9.4. Определение. Рангом матрицы называется порядок ее базисного минора. Ранг матрицы обозначаетсяили.

Замечание.

Отметим, что в силу равноправности строк и столбцов определителя ранг матрицы не меняется при ее транспонировании.

4.9.5. Теорема. (Инвариантность ранга матрицы относительно элементарных преобразований)

Ранг матрицы не меняется при ее элементарных преобразованиях.

Без доказательства.

4.9.6. Теорема. (О базисном миноре).

Базисные строки (столбцы) линейно независимы. Всякая строка (столбец) матрицы может быть представлена в виде линейной комбинации ее базисных строк (столбцов).

Доказательство:

Проведем доказательство для строк. Доказательство утверждения для столбцов может быть проведено по аналогии.

Пусть ранг матрицы размеровравен, а− базисный минор. Без ограничения на общность предположим, что базисный минор расположен в левом верхнем углу (в противном случае можно привести матрицу к этому виду с помощью элементарных преобразований):

.

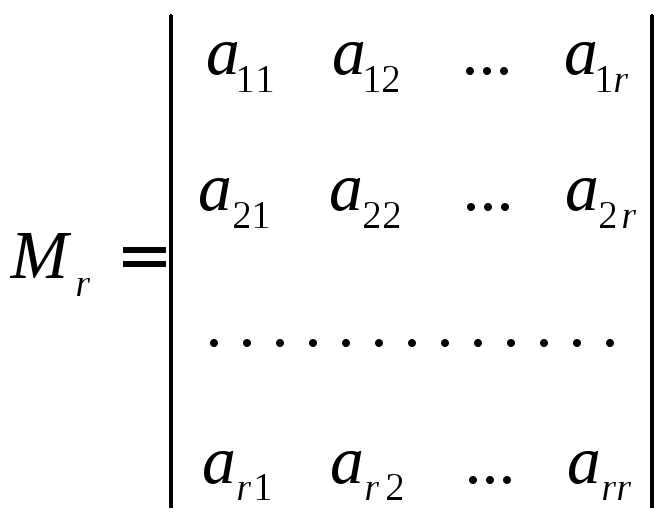Докажем сначала линейную независимость базисных строк. Доказательство проведем от противного. Предположим, что базисные строки линейно зависимы. Тогда согласно теореме 4.8.4 одна из строк может быть представлена в виде линейной комбинации остальных базисных строк. Следовательно, если вычесть из этой строки указанную линейную комбинацию, то мы получим нулевую строку, а это означает, что минор равен нулю, что противоречит определению базисного минора. Таким образом, мы получили противоречие, следовательно, линейная независимость базисных строк доказана.

Докажем теперь, что всякая строка матрицы может быть представлена в виде линейной комбинации базисных строк. Если номер рассматриваемой строки от 1 доr, то тогда, очевидно, она может быть представлена в виде линейной комбинации c коэффициентом, равным 1 при строке и нулевыми коэффициентами при остальных строках. Покажем теперь, что если номер строкиотдо, она может быть представлена в виде линейной комбинации базисных строк. Рассмотрим минор матрицы, полученный из базисного минорадобавлением строкии произвольного столбца:

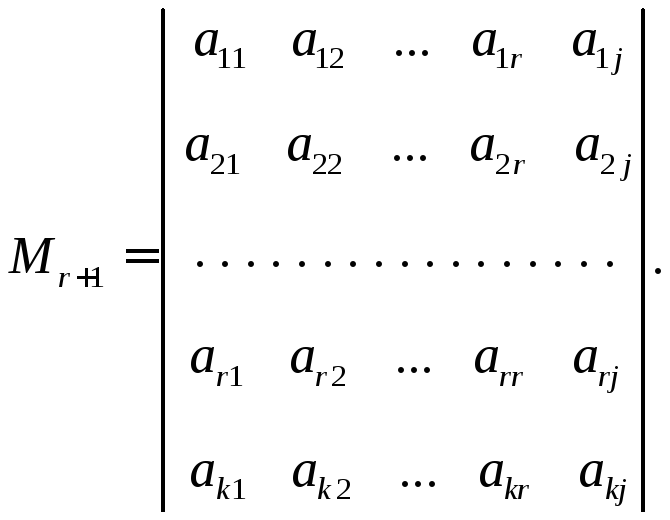
Покажем, что данный минор равен нулю для любого номера строкиотдои для любого номера столбцаот 1 до.

Действительно, если номер столбца от 1 доr, то имеем определитель с двумя одинаковыми столбцами, который, очевидно, равен нулю. Если же номер столбца отr+1 до , а номер строкиотдо, тоявляется минором исходной матрицы большего порядка, чем базисный минор, а это означает, что он равен нулю из определения базисного минора. Таким образом, доказано, что минорравен нулю для любого номера строкиотдои для любого номера столбцаот 1 до. Разлагая его по последнему столбцу, получим:

Здесь − соответствующие алгебраические дополнения. Заметим, что, так как следовательно,является базисным минором. Следовательно, элементы строкиk могут быть представлены в виде линейной комбинации соответствующих элементов базисных строк с коэффициентами, не зависящими от номера столбца :

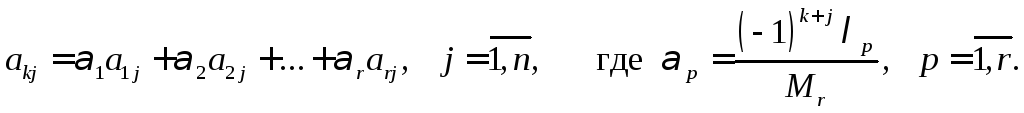
Таким образом, мы доказали, что произвольная строка матрицы может быть представлена в виде линейной комбинации ее базисных строк. Теорема доказана.

Лекция 13

4.9.7. Теорема. (О ранге невырожденной квадратной матрицы)

Для того, чтобы квадратная матрица являлась невырожденной, необходимо и достаточно, чтобы ранг матрицы равен размеру этой матрицы.

Доказательство:

Необходимость. Пусть квадратная матрица размераn является невырожденной, тогда , следовательно, определитель матрицы является базисным минором, т.е.

Достаточность. Пусть тогда порядок базисного минора равен размеру матрицы, следовательно, базисным минором является определитель матрицы, т.е.по определению базисного минора.

Следствие.

Для того, чтобы квадратная матрица была невырожденной, необходимо и достаточно, чтобы ее строки были линейно независимыми.

Доказательство:

Необходимость. Так как квадратная матрица является невырожденной, то ее ранг равен размеру матрицы то есть определитель матрицы является базисным минором. Следовательно, по теореме 4.9.6 о базисном миноре строки матрицы являются линейно независимыми.

Достаточность. Так как все строки матрицы линейно независимы, то ее ранг не меньше размера матрицы, а значит, следовательно, по предыдущей теореме 4.9.7 матрицаявляется невырожденной.

4.9.8. Метод окаймляющих миноров для нахождения ранга матрицы.

Заметим, что частично этот метод уже был неявно описан в доказательстве теоремы о базисном миноре.

4.9.8.1. Определение. Минор называетсяокаймляющим по отношению к минору , если он получен из минорадобавлением одной новой строки и одного нового столбца исходной матрицы.

4.9.8.2. Процедура нахождения ранга матрицы методом окаймляющих миноров.

1. Находим какой-либо текущий минор матрицы отличный от нуля.

2. Вычисляем все окаймляющие его миноры.

3. Если все они равны нулю, то текущий минор является базисным, и ранг матрицы равен порядку текущего минора.

4. Если среди окаймляющих миноров находится хотя бы один отличный от нуля, то он полагается текущим и процедура продолжается.

Пример.

Найдем с помощью метода окаймляющих миноров ранг матрицы

.

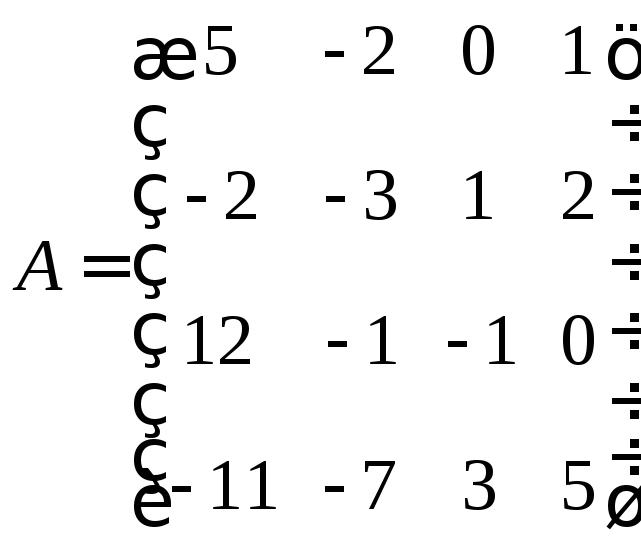Легко указать текущий минор второго порядка, отличный от нуля, например,

.

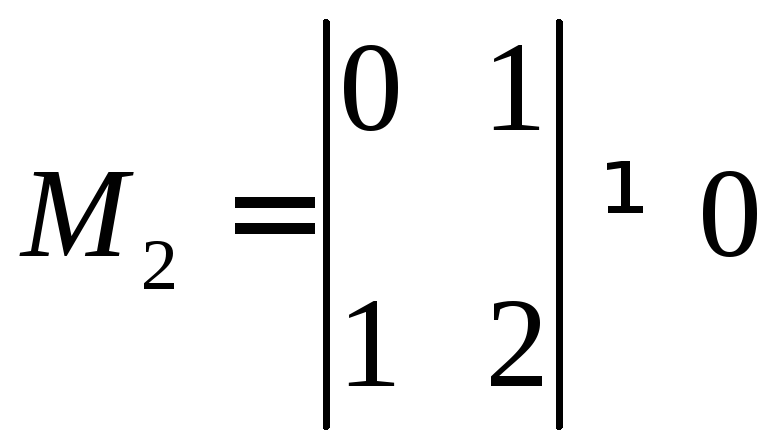Вычисляем окаймляющие его миноры:

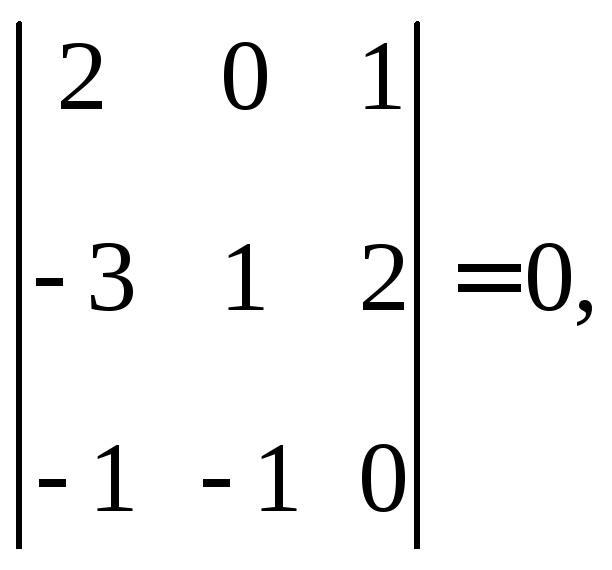
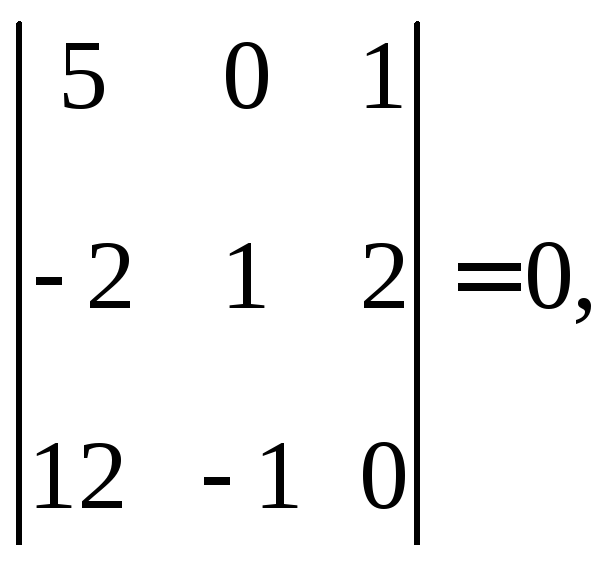
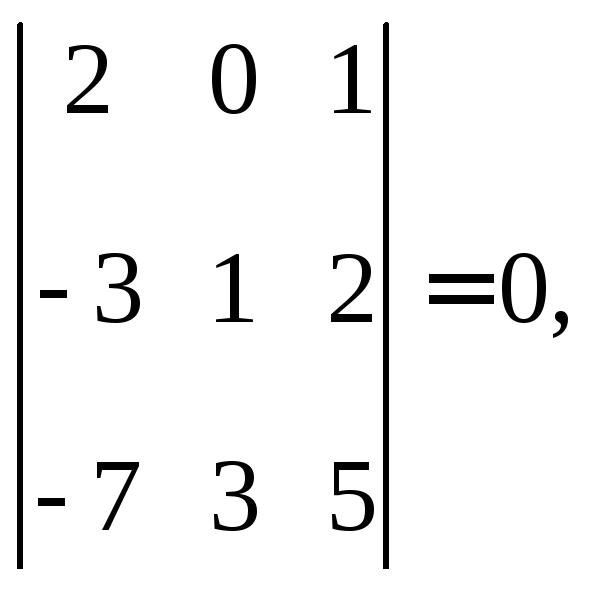
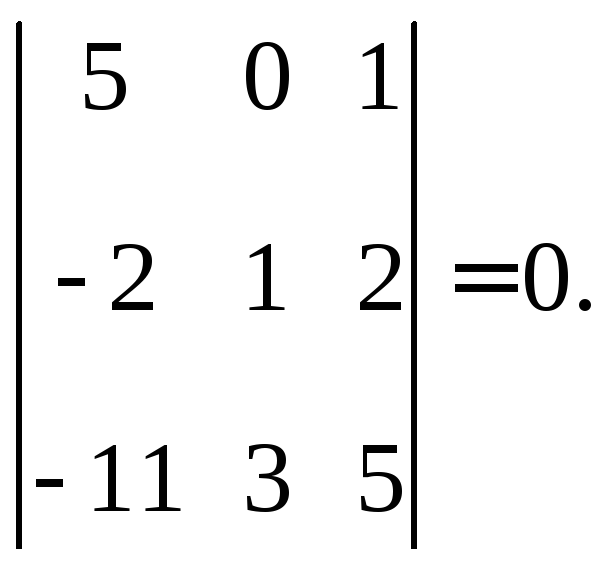
Следовательно, так как все окаймляющие миноры третьего порядка равны нулю, то минор является базисным, то есть

Замечание. Из рассмотренного примера видно, что метод является достаточно трудоемким. Поэтому на практике гораздо чаще используется метод элементарных преобразований, речь о котором пойдет ниже.

4.9.9. Нахождение ранга матрицы методом элементарных преобразований.

На основании теоремы 4.9.5 можно утверждать, что ранг матрицы не меняется при элементарных преобразованиях (то есть ранги эквивалентных матриц равны). Поэтому ранг матрицы равен рангу ступенчатой матрицы, полученной из исходной элементарными преобразованиями. Ранг же ступенчатой матрицы, очевидно, равен количеству ее ненулевых строк.

Пример.

Определим ранг матрицы

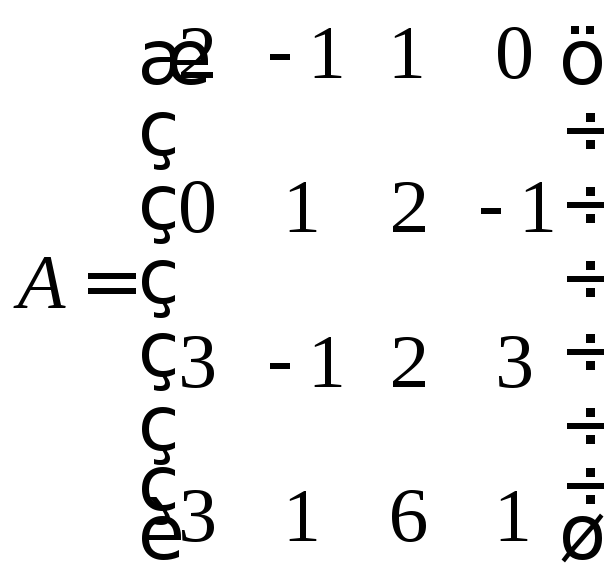
методом элементарных преобразований.

Приведем матрицу к ступенчатому виду:

Количество ненулевых строк полученной ступенчатой матрицы равно трем, следовательно,

4.9.10. Ранг системы векторов линейного пространства.

Рассмотрим систему векторов некоторого линейного пространства. Если она является линейно зависимой, то в ней можно выделить линейно независимую подсистему.

4.9.10.1. Определение. Рангом системы векторов линейного пространстваназывается максимальное количество линейно независимых векторов этой системы. Ранг системы векторовобозначается как.

Замечание. Если система векторов линейно независима, то ее ранг равен количеству векторов системы.

Сформулируем теорему, показывающую связь понятий ранга системы векторов линейного пространства и ранга матрицы.

4.9.10.2. Теорема. (О ранге системы векторов линейного пространства)

Ранг системы векторов линейного пространства равен рангу матрицы, столбцами или строками которой являются координаты векторов в некотором базисе линейного пространства.

Без доказательства.

Следствие.

Для того, чтобы система векторов линейного пространства являлась линейно независимой, необходимо и достаточно, чтобы ранг матрицы, столбцами или строками которой являются координаты векторов в некотором базисе, был равен количеству векторов системы.

Доказательство очевидно.

4.9.10.3. Теорема (О размерности линейной оболочки).

Размерность линейной оболочки векторов линейного пространстваравна рангу этой системы векторов:

Без доказательства.