Лекция 10.

Глава 4. Матрицы.

В этой главе мы рассмотрим основные виды матриц, операции над ними, понятие ранга матрицы и их приложения к решению систем линейных алгебраических уравнений.

§4.1. Основные понятия.

4.1.1. Определение. Матрицей размеров называется прямоугольная таблица чисел, содержащаястрок истолбцов. Числаиназываютсяразмерами матрицы. Введем обозначение матрицы

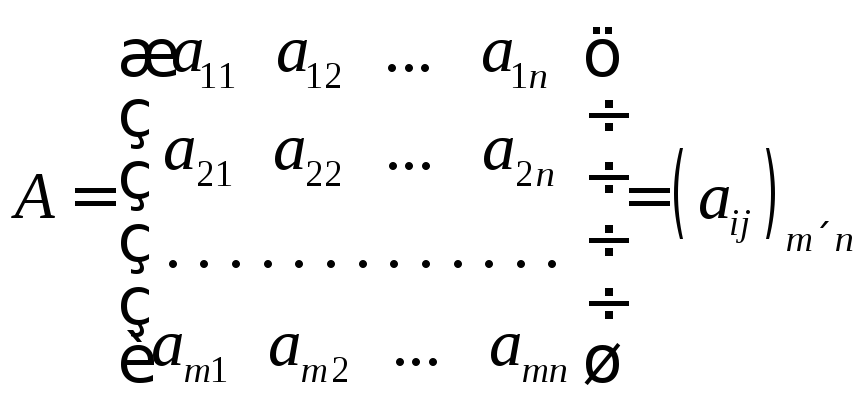
Числа ,называютсяэлементамиматрицы. Таким образом, элемент

расположен на пересечении строкии столбца.

4.1.2. Определение.Две матрицыиодинаковых размеров называютсяравными, если все их соответствующие элементы равны между собой, т.е.

4.1.3. Определение.Матрица, все элементы которой равны нулю, называетсянулевойи обозначается:,

4.1.4. Определение. Матрица называется квадратной, если количество ее строк равно количеству столбцов, т.е. .

4.1.5. Определение. Главной диагональю квадратной матрицы называется диагональ, идущая из левого верхнего угла в правый нижний угол.

4.1.6. Определение. Побочной диагональю квадратной матрицы называется диагональ, идущая из правого верхнего угла в левый нижний угол.

4.1.7. Определение. Квадратная матрица называется верхней треугольной, если все ее элементы, расположенные под главной диагональю, равны нулю.

4.1.8. Определение. Квадратная матрица называется нижней треугольной, если все ее элементы, расположенные над главной диагональю, равны нулю.

4.1.9. Определение. Квадратная матрица называется диагональной, если все ее элементы, отличные от нуля, расположены на главной диагонали.

4.1.10. Определение. Диагональная матрица называется скалярной, если все ее элементы, расположенные на главной диагонали, равны между собой.

4.1.11. Определение. Диагональная матрица называется единичной, если все ее элементы, расположенные на главной диагонали, равны единице. Единичная матрица обозначается . Таким образом,

4.1.12. Определение. Матрица называется ступенчатой, если для любой ее строки под первым слева ненулевым элементом и предшествующими ему нулевыми элементами строки все элементы матрицы равны нулю.

Примеры:

или .

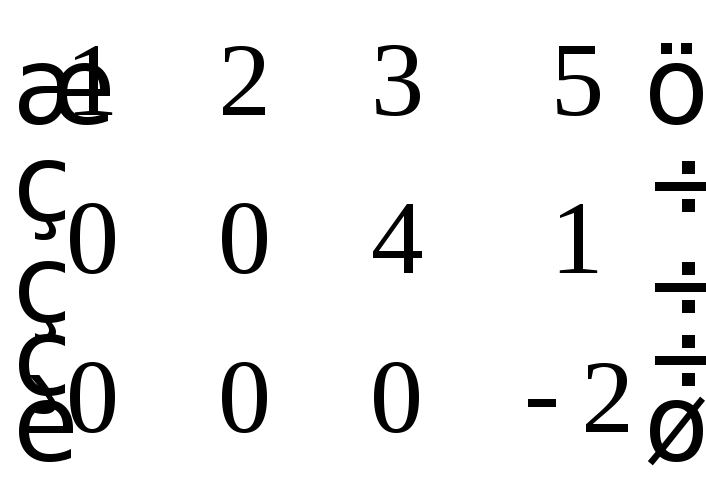4.1.13. Определение. Операция над матрицей размеров , в результате которой ее строки и столбцы меняются местами с сохранением порядка следования, называется операциейтранспонирования. Матрица размеров , полученная в результате транспонирования матрицы, называется транспонированной по отношению к ней и обозначается . При этом

Замечание. Легко показать, что в результате повторного транспонирования мы получим исходную матрицу, т.е. .

§4.2. Линейные операции над матрицами

4.2.1. Определение. Суммой матриц иодинаковых размеров называется матрицатех же размеров, каждый элемент которой равен сумме соответствующих элементов матрици:

,

Замечание. Операция сложения матриц определена только для матриц одинаковых размеров. Если размеры двух матриц не совпадают, то операция их сложения не определена.

4.2.2. Теорема. (Свойства операции сложения матриц)

Для произвольных матриц ,,одинаковых размеровсправедливы следующие свойства:

1.

2.

3. ;

4. .

Доказательство этих очевидных свойств непосредственно вытекает из определения операции сложения матриц.

4.2.3. Определение. Разностью матриц иодинаковых размеров называется матрицатех же размеров, такая, что.

4.2.4. Определение. Произведением матрицы размеровна числоназывается матрицатех же размеров, каждый элемент которой равен произведению соответствующего элемента матрицына число:

,

4.2.5. Теорема. (Свойства операции умножения матрицы на число)

Для произвольных матриц иодинаковых размерови любых действительных чиселсправедливы следующие свойства:

1.

2.

3.

4.

Доказательство очевидным образом вытекает из определений 4.2.1 и 4.2.4.

Замечание. Из приведенных свойств ясно, что множество матриц размеров образует линейное пространство относительно введенных операций сложения матриц и их умножения на числа. В качестве базиса можно, например, взять

, … ,.

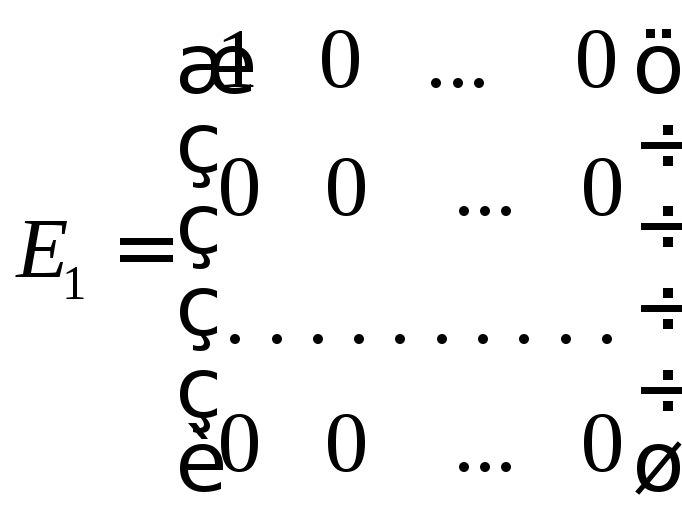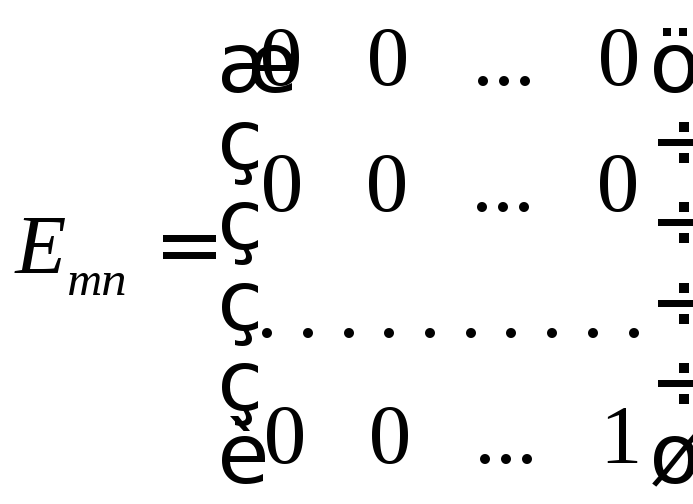Очевидно, любая матрица размеров может быть представлена в виде линейной комбинации приведенных базисных матриц Таким образом, размерность этого линейного пространства