Календарные планы / 2 курс / 4 семестр / ФН / Функциональный анализ / Функциональный анализ_ФН4_Оценочные средства и рейтинг

Функциональный анализ и интегральные уравнения

ФН-2

Функциональный анализ и интегральные уравнения

Для ФН4

Рейтинговая система контроля освоения дисциплины

Планируемые КМ	Объем, час	Неделя проведения	Оценка в баллах
			Максимальная	Минимальная
Семестр 4
ДЗ №1	10	5	30	18
Модуль 1		5	30	18
РК №1	4	10	30	18
Модуль 2		10	30	18
ДЗ №2	10	15	20	12
РК №2	4	15	20	12
Модуль 3		15	40	24
Итоговый рейтинг			100	60

Шкала перевода рейтинговых оценок по всем видам занятий и самостоятельной работы в зачетную оценку:

Рейтинг	Зачетная оценка
60 – 100	зачет
0 – 59	незачет

Типовые варианты заданий

Домашнее задание №1 «Основные понятия функционального анализа

Домашнее задание №2 «Функционалы, операторы, интегральные уравнения»

Рубежный контроль №1

Рубежный контроль №2

Вопросы для подготовки к рубежным контролям

МОДУЛЬ 1: Метрические и номированные пространства

1. Определение метрических пространств. Примеры основных метрических пространств (С[a,b], m,)

2. Неравенство Гельдера.

3. Неравенство Минковского.

4. Полные метрические пространства. Доказать теорему о вложенных шарах.

5. Доказать теорему о сжимающих отображениях.

6. Свойства оператора Вольтерра и его степени.

7. Сепарабельные пространства.

2. Компактные множества в метрических пространствах.

3. Свойства непрерывных функций, заданных на компактных множествах.

4. Критерии относительной компактности в пространствах

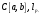
5. Определение нормированных пространств, банаховых пространств. Расстояние от точки до подпространства.

6. Сходимость рядов в нормированных и банаховых пространствах. Критерий Коши сходимости ряда. Абсолютная сходимость рядов в банаховых пространствах.

7. Счетные базисы в банаховых пространствах.

МОДУЛЬ 2: Гильбертовы пространства и линейные функционалы

2. Определение гильбертовых пространств. Доказать теорему о предельном переходе в скалярном произведении и равенство параллелограмма.

3. Определение ортогональных элементов в гильбертовом пространстве. Теорема о разложении гильбертова пространства в ортогональную сумму.

4. Ортонормированные системы. Ряды Фурье в гильбертовых пространствах. Доказать теорему о расстоянии от элемента до подпространства, являющегося линейной оболчкой n первых элементов ортонормированной системы. Доказать неравенство Бесселя.

5. Определение ортонормированного базиса гильбертова пространства. Критерий базисности ортонормированной системы в гильбертовом пространстве (любой элемент есть сумма своего ряда Фурье).

6. Равенство Парсеваля как критерий базисности ортонормированной системы в гильбертовом пространстве.

7. Замкнутость ортонормированной системы как критерий ее базисности в гильбертовом пространстве.

8. Полные ортонормированные системы. Полнота ортонормированной системы как критерий ее базисности в гильбертовом пространстве.

9. Теорема о существовании счетного ортонормированного базиса в сепарабельном гильбертовом пространстве.

10. Теорема об изоморфизме всех гильбертовых сепарабельных пространств.

МОДУЛЬ 3: линейные операторы и интегральные уравнения

2. Определение линейного ограниченного функционала. Cвязь непрерывности и ограниченности линейного функционала.

3. Норма линейного ограниченного функционала. Равносильность различных определений нормы. Связь понятий непрерывности и ограниченности для линейного функционала.

4. Сопряженное пространство. Слабая и сильная сходимости.

5. Общий вид линейного непрерывного функционала в гильбертовом пространстве.

7. Обобщенные функции. Определение и свойства.

2. Линейные операторы. Непрерывность, ограниченность линейных операторов и их связь. Пространство линейных операторов.

3. Обратный оператор. Теорема Банаха. Примеры.

4. Сопряженный и самосопряженный операторы в гильбертовом пространстве.

5. Спектр оператора. Резольвента. Теоремы о регулярных значениях оператора и о его спектре.

6. Компактные операторы в банаховых пространствах, их свойства. Теоремы о собственных элементах компактного оператора. Спектр компактного оператора.

7. Самосопряженные компактные операторы в гильбертовом пространстве и их свойства. Теорема Гильберта - Шмидта.

8. Интегральные уравнения Фредгольма. Оператор Гильберта – Шмидта, его компактность и оценка нормы. Сопряженный оператор.

9. Интегральные уравнения Фредгольма с симметрическими ядрами и их решения.

10. Решение интегральных уравнений Фредгольма с вырожденными ядрами.

Рейтинговые оценки

за выполнение отдельных позиций заданий контрольного мероприятия

Модуль 1

Контрольное мероприятие	Количество заданий	Баллы за задание
ДЗ №1	4 задачи	0; 1; 2

Шкала перевода в рейтинговую оценку:

Набранные баллы	Оценка	Рейтинг
0-5	2 (неуд.)	0
6	3 (удовл.)	18
7	4 (хор.)	24
8	5 (отл.)	30

Модуль 2

Контрольное мероприятие	Количество заданий	Баллы за задание
РК №1	1 теория и 3 задачи	теория – 0; 1; 2; 3; 4 задачи - 0; 1; 2; 3; 4

Шкала перевода в рейтинговую оценку:

Набранные баллы	Оценка	Рейтинг
0-9	2 (неуд.)	0
10-12	3 (удовл.)	18
13-14	4 (хор.)	24
15-16	5 (отл.)	30

Модуль 3

Контрольное мероприятие	Количество заданий	Баллы за задание
ДЗ №2	4 задачи	0; 1; 2

Шкала перевода в рейтинговую оценку:

Набранные баллы	Оценка	Рейтинг
0-5	2 (неуд.)	0
6	3 (удовл.)	12
7	4 (хор.)	16
8	5 (отл.)	20

6дуль 2с выррожденными ядрами.ентами в метрическом пространстве

Контрольное мероприятие	Количество заданий	Баллы за задание
РК №2	12 задач в форме тестов	задачи - 0; 1

Шкала перевода в рейтинговую оценку:

Набранные баллы	Оценка	Рейтинг
0-8	2 (неуд.)	0
9-10	3 (удовл.)	12
11	4 (хор.)	16
12	5 (отл.)	20

35