Модуль 2: линейные операторы и интегральные уравнения

28. Определения полукольца, кольца, - кольца, - алгебры. Определение меры, счетно-аддитивной меры. Продолжение меры с полукольца на минимальное кольцо, порожденное полукольцом. Доказать свойства меры и счетно-аддитивной меры.

29. Внешняя мера, счетная полуаддитивность внешней меры.

30. Лебегово продолжение меры. Измеримые по Лебегу множества и их свойства.

31. Доказать теорему о непрерывности меры Лебега.

32. Измеримые функции и их свойства. Доказать измеримость суммы, разности, произведения и частного измеримых функций. Доказать измеримость предела измеримых функций.

33. Интеграл Лебега от простых функций и его свойства.

34. Общее определение интеграла Лебега и его свойства.

35. Доказать неравенство Чебышева.

36. Доказать абсолютную непрерывность интеграла Лебега.

37. Пространства суммируемых функций , , .

38. Определение линейного ограниченного функционала. Cвязь непрерывности и ограниченности линейного функционала.

39. Норма линейного ограниченного функционала. Равносильность различных определений нормы. Связь понятий непрерывности и ограниченности для линейного функционала.

40. Теорема Хана-Банаха (формулировка). Доказать следствия.

41. Сопряженное пространство. Слабая и сильная сходимости. Второе сопряженное пространство.

42. Общий вид линейного непрерывного функционала в гильбертовом пространстве.

2. Обобщенные функции. Определение и свойства.

43. Линейные операторы. Непрерывность, ограниченность линейных операторов и их связь. Пространство линейных операторов.

44. Обратный оператор. Теорема Банаха. Примеры. Доказать теорему о необходимом и достаточном условии существования обратного оператора.

45. Сопряженный оператор. Доказать теорему о линейности, ограниченности сопряженного оператора и о его норме.

46. Сопряженный и самосопряженный операторы в гильбертовом пространстве. Пример линейного ограниченного интегрального оператора, действующего в пространстве 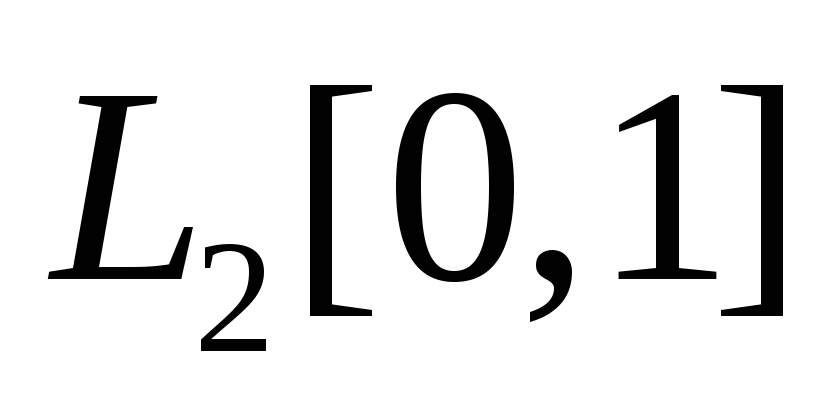, с непрерывным ядром. Сопряженный оператор к этому оператору.

47. Спектр оператора. Резольвента. Теоремы о регулярных значениях оператора и о его спектре.

48. Компактные операторы в банаховых пространствах, их свойства. Теоремы о собственных элементах компактного оператора. Спектр компактного оператора.

49. Самосопряженные компактные операторы в гильбертовом пространстве и их свойства. Теорема Гильберта - Шмидта.

50. Интегральные уравнения Фредгольма. Оператор Гильберта – Шмидта, его компактность и оценка нормы. Сопряженный оператор.

51. Интегральные уравнения Фредгольма с симметрическими ядрами и их решения.

52. Решение интегральных уравнений Фредгольма с вырожденными ядрами.

53. Теоремы Фредгольма для уравнений с произвольными ядрами.

Рейтинговые оценки за выполнение отдельных позиций заданий контрольного мероприятия

Модуль 1

Контрольное мероприятие	Количество заданий	Баллы за задание
ДЗ №1	4 задачи	0; 1; 2

Шкала перевода в рейтинговую оценку:

Набранные баллы	Оценка	Рейтинг
0-5	2 (неуд.)	0
6	3 (удовл.)	3
7	4 (хор.)	4
8	5 (отл.)	5

Контрольное мероприятие	Количество заданий	Баллы за задание
РК №1	1 теория и 3 задачи	теория – 0; 1; 2; 3; 4 задачи - 0; 1; 2; 3; 4

Шкала перевода в рейтинговую оценку:

Набранные баллы	Оценка	Рейтинг
0-9	2 (неуд.)	0
10-12	3 (удовл.)	17
13-14	4 (хор.)	20
15-16	5 (отл.)	23

Модуль 2

Контрольное мероприятие	Количество заданий	Баллы за задание
ДЗ №2	4 задачи	0; 1; 2

Шкала перевода в рейтинговую оценку:

Набранные баллы	Оценка	Рейтинг
0-5	2 (неуд.)	0
6	3 (удовл.)	3
7	4 (хор.)	4
8	5 (отл.)	5

Контрольное мероприятие	Количество заданий	Баллы за задание
Контрольная работа	1 теория и 4 задачи в форме тестов	теория – 0; 1; 2; 3; 4 задачи - 0; 1

Шкала перевода в рейтинговую оценку:

Набранные баллы	Оценка	Рейтинг
0-3	2 (неуд.)	0
4-5*	3 (удовл.)	9
6-7	4 (хор.)	11
8	5 (отл.)	14

^* не менее двух баллов за задачи

Контрольное мероприятие	Количество заданий	Баллы за задание
Рубежный контроль	15 задач в форме тестов	задачи - 0; 1

Шкала перевода в рейтинговую оценку:

Набранные баллы	Оценка	Рейтинг
0-11	2 (неуд.)	0
12-13	3 (удовл.)	12
14	4 (хор.)	15
15	5 (отл.)	19

46