
ТСД. Лекции Силантьевой / лекция_граф_3_14
.docЭЙЛЕРОВЫ ПУТИ И ЦИКЛЫ.
Произвольный путь в графе, проходящий через каждое ребро графа точно один раз, называется ЭЙЛЕРОВЫМ ПУТЕМ. (По вершинам путь может проходить неоднократно, то есть путь может быть не простой). Это значит, что в пути v(1)-v(2)-...-v(m+1) каждое ребро графа появляется один и только один раз как { v(i),v(i+1) } для некоторого i. Если при этом v(1)=v(m+1), то имеем ЭЙЛЕРОВ ЦИКЛ.
Для существования эйлерова пути в связном графе необходимо и достаточно, чтобы граф содержал не более 2 вершин нечетной степени.
В алгоритме поиска эйлерова цикла связный граф G=<V,E> описан двунаправленным списками ZAP[v], а эйлеров цикл представлен последовательностью вершин в рабочем стеке ST; стек SE содержит последовательность полностью обработанных вершин.
Procedure EULER;
Begin
ST <-- 0; SE <-- 0;
 v
<-- произвольная вершина графа G;
v
<-- произвольная вершина графа G;
ST <-- v; {помещаем ее в рабочий стек ST }
While ST<>0 do {пока стек не пуст}
Begin
v <-- upper(ST); {в v - верхний элемент рабочего стека}
If ZAP[v]<>0 {если есть смежные вершины с v}
Then
Begin
u <-- 1-я вершина списка ZAP[v]; {помещаем 1-ю из списка в u}
ST <-- u; {ее помещаем в раб. стек}
ZAP[v] <-- ZAP[v] \ {u}; {удаление ребра v--u из списка для v}
ZAP[u] <-- ZAP[u] \ {v}; {удаление ребра v--u из списка для u}
v<--u {проверяем следующую вершину}
End
Else {иначе, список ZAP[v] пуст}
Begin
v <-- ST; { удаляем вершину v из стека ST}
SE <-- v { помещаем ее в стек SE }
End
End
End.
Сначала выбирается произвольная вершина v. Если есть нечетные, то одна из них.
Вершины с нечетной степенью должны быть конечными (можно их перенумеровать).
В цикле по условию опустошения стека ST строится путь с началом в v.
Вершины строящегося пути размещаются в ST, ребра, входящие в путь, удаляются из графа (соответствующие элементы удаляются из списков ZAP).
Двунапрнавленность списков инцидентности ZAP[v] позволяет устранить ребро {v,u} за время, ограниченное константой. Общая сложность алгоритма: O(m), где m – количество ребер графа.
4
Д ля
графа
ля
графа
1 3 5


2 14



3 13 12 11

4 15 6


5 2


6 8 10 7

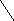
7

 -> 2, 6, 8, 9
-> 2, 6, 8, 9
8 1 9
9 -> 6, 9
один из найденных эйлеровых циклов представлен последовательностью вершин: 1–2 –3 – 4 – 5 – 6 –7– 2 – 8 – 6 – 9 –7 – 8 – 5 –3 – 1. ST –Эйлеров путь
SE 4 – 2 – 7 - 9 – 6 – 8 – 5 – 3 – 1 - последов. обработанных вершин
Гамильтоновы пути в графе (алгоритмы с возвратом)
Пусть
![]() - некоторый граф. Он называется
гамильтоновым,
если в нем
существует простой цикл, содержащий
все вершины графа. Например, каждый
полный граф – гамильтонов, потому что
в нем проведены всевозможные ребра и,
в частности, те, благодаря кот. возможен
обход по всем вершинам. А вот пример
графа, не являющегося гамильтоновым:
- некоторый граф. Он называется
гамильтоновым,
если в нем
существует простой цикл, содержащий
все вершины графа. Например, каждый
полный граф – гамильтонов, потому что
в нем проведены всевозможные ребра и,
в частности, те, благодаря кот. возможен
обход по всем вершинам. А вот пример
графа, не являющегося гамильтоновым:






Общих и легко осуществляемых действий, с помощью кот. можно было бы достоверно выяснить, является ли данный граф гамильтоновым, не существует. Но, имеются достаточные условия на гамильтоновость, кот. проверить легко. Недостаток - даже если ни одно из этих условий не выполняется, граф м.б. гамильтоновым.
Рассмотрим построение путей в графе, проходящих в точности один раз через каждую вершину (а не каждое ребро) графа. Такой путь и соответствующий цикл называются Гамильтоновыми и существуют не для каждого графа, как и Эйлеров путь. Например, в графе:
1

 –> 2, 3
–> 2, 3
2

 –> 1, 3, 4, 5
–> 1, 3, 4, 5
3


 –> 1, 2, 6
–> 1, 2, 6
4 –> 2, 6
–> 2, 6
5
 -> 2, 6, 7
-> 2, 6, 7
6

 -> 3, 4, 5, 7
-> 3, 4, 5, 7
7 -> 5,6
-> 5,6
есть гамильтонов путь 1, 3, 2, 4, 6, 5, 7. В то же время в графе
1 -> 2, 3, 4
-> 2, 3, 4
2
 -> 1, 5
-> 1, 5
3 -> 3, 5
4


 -> 1, 5
-> 1, 5
5

 -> 2, 3, 4, 6
-> 2, 3, 4, 6
6
 -> 5
-> 5
г амильтонова
пути не существует.
амильтонова
пути не существует.
В отличие от эйлеровых путей неизвестно ни одного простого необходимого и достаточного условия для существования гамильтоновых путей.
. Условия Дирака, Оре и Поша, гарантирующие существование в графе гамильтонова цикла.
условие
Дирака.
Пусть
![]() - число вершин в данном графе; если
степень каждой вершины не меньше, чем
- число вершин в данном графе; если
степень каждой вершины не меньше, чем
![]() ,
то граф называется графом
Дирака. Можно
доказать, что каждый
граф Дирака обязательно гамильтонов.
,
то граф называется графом
Дирака. Можно
доказать, что каждый
граф Дирака обязательно гамильтонов.
пример графа Дирака:







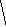
Очевидно, этот граф - гамильтонов. А вот пример гамильтонова графа, не являющегося графом Дирака:





условие
Оре. Если
для любой пары несмежных вершин
![]() выполнено неравенство
выполнено неравенство
![]() ,
то граф называется графом
Оре Можно
доказать, что всякий
граф Оре обязательно гамильтонов.
,
то граф называется графом
Оре Можно
доказать, что всякий
граф Оре обязательно гамильтонов.
пример графа Оре:









пример графа, не являющегося графом Оре, но граф гамильтонов:




Нетрудно заметить, что всякий граф Дирака автоматически является графом Оре. Но вот пример графа Оре, не являющегося графом Дирака:






условие
Поша..
Введем следующую функцию
![]() целого неотрицательного аргумента
целого неотрицательного аргумента
![]() .
Сначала запишем определение формулой,
речь идет о графе
.
Сначала запишем определение формулой,
речь идет о графе
![]() ,
,
для
которого строится функция
![]() :
:
![]() ;
;
написанное
означает, что функция
![]() в каждом целом неотрицательном
в каждом целом неотрицательном
![]() принимает значение, равное количеству
вершин графа
принимает значение, равное количеству
вершин графа
![]() ,
степень которых не превосходит
,
степень которых не превосходит
![]() .
.
Такую
функцию
![]() называют функцией
Поша графа
называют функцией
Поша графа
![]() .
.
построим функцию Поша следующего графа:




Функция будет описана таблично:
-
X
0
1
2
3
4
5
...
f(x)
0
1
3
4
4
4
...
Теперь сформулируем условие Поша.
Графом
Поша называется
граф
![]() ,
удовлетряющий следующим условиям (число
вершин этого графа обозначим через
,
удовлетряющий следующим условиям (число
вершин этого графа обозначим через
![]() ,
его функцию Поша обозначим через
,
его функцию Поша обозначим через
![]() ,
,
![]() будет обозначать целое число):
будет обозначать целое число):
1)
для
![]() выполняется неравенство
выполняется неравенство
![]() ;
;
2)
если
![]() - целое число, то при
- целое число, то при
![]() имеет место неравенство:
имеет место неравенство:
![]() .
.
Можно доказать, что каждый граф Поша обязательно гамильтонов. Легко заметить, что простой цикл на большом числе вершин, графом Поша не является, но, конечно, явяляется га-мильтоновым графом.
Кр. того, нетрудно заметить, что всякий граф Дирака является графом Поша, каждый граф Оре является графом Поша. Обратное в обоих последних случаях неверно. Вот пример: фиксируем какой-нибудь полный граф на достаточно большом числе вершин; добавим к нему еще одну вершину и соединим ее с любыми двумя вершинами в исходном графе; очевидно, вновь полученный граф - гамильтонов; фиксируем в нем к.-н. гамильтонов цикл и удалим из графа какое-нибудь ребро, не включенное в этот цикл; полученный в результате граф будет, как нетрудно проверить, графом Поша; однако, он не будет графом Оре - будут сразу две пары несмежных вершин, сумма степеней которых меньше числа вершин в графе.
Неизвестен даже алгоритм полиномиальной сложности, проверяющий существование гамильтонова пути в произвольном графе. Проблема существования гамильтонова пути принадлежит к классу т.н. NP-полных задач.
Т.е. полный перебор, т.е. n!*n шагов. Для сокращения перебора был разработан класс алгоритмов «с возвратом» (backtracking).
Рассмотрим алгоритм поиска всех гамильтоновых циклов в графе (в глобальном векторе X строится последовательность вершин X[1],…X[k-1] строящегося пути; логический вектор DOP показывает, можно ли вставить вершины в проектируемый путь, n – кол-во вершин графа):
Procedure Ham(k); {}
Begin
For uZAP[X[k-1]] do
If (k=n+1) {если все вершины уже вставлены в путь}
And (u=v0) {и если последняя в-на в пути совпадает с 1-ой}
{т.е. это цикл}
Then Write(X[1],…X[k-1],v0) {печать пути и возможное окончание
алгоритма}
Else
If DOP[u] {если вершину можно вставить в путь}
Then
Begin
X[k] u; DOP[u] False;
If k<= n Then
Ham(k+1); {очередное удлинение пути привело в тупик –}
Else
DOP[u] True;
{необходимо вернуться для следующей попытки}
End;
End; {Ham}
Begin
For vV do DOP[v] True; {инициализация}
X[1] v0; {v0 – произвольная фиксированная вершина графа}
DOP[v0] False;
Ham(2); {начало построения пути длиной 2}
End.
Этот рекурсивный алгоритм имеет сложность не более чем exp(n)
Работу этого алгоритма можно проиллюстрировать процессом поиска в некотором дереве, состоящем из всех возможных последовательностей <x1,…,xk> для графа.
