Этап 2.

5. Шаг 1. Находим управление и состояние .

6. Шаг 2. Находим управление и состояние .

7. …………………..

8. Шаг N. Находим управление и состояние =●

Заметим, что при приближенном решении задач оптимального управления методом динамического программирования остается открытым вопрос о сходимости решения к решениюисходной непрерывной задачи оптимального управления (1), (2).

Пример 1. Решим методом динамического программирования Беллмана задачу оптимального управления

, (8)

, (9)

где - символ целой части числа (т.е. множествоесть множество целых числе от 0 до 4).

Подобно (3), (4) заменим ОДУ (11) его конечно-разностным аналогом

, (10)

а функционал (9) - его приближенным значением, вычисленным по формуле прямоугольников

. (11)

Положим, что .

Обратим внимание на следующее обстоятельство: из (8) и условия следует, что фазовая переменнаяможет принимать только целочисленные значения в интервале.

Этап 1.

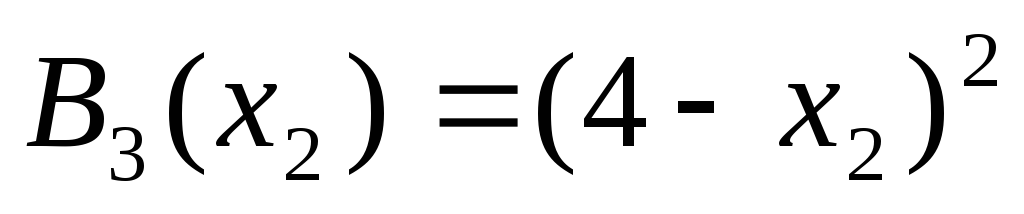1. Шаг 1 . Из условия (6) находим условно оптимальное управление и функцию Беллмана=. Из выражения (8) следует, что. Поэтомуи. Сведем результаты вычисления значений функциив таблицу 1. Прочерки в таблице соответствуют не допустимым управлениям; значения управления и функции Беллмана, выделенные жирным, соответствует оптимальной траектории.

Таблица 1 - Значения функции Беллмана

		0	1	2	3	4
4		4	3	2	1	0
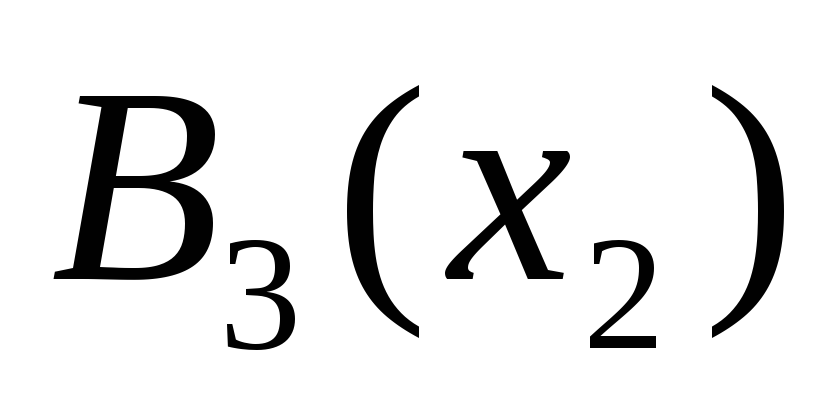
		16	9	4	1	0

2. Шаг 2 .Используя результаты предыдущего шага, из условия (7) находим условно оптимальное управление и функцию Беллмана=- таблица 2.

Рассмотрим, для примера, схему получения значений ,, соответствующих переходу системы из состоянияв состояние. Из состоянияв состояниесистема переходит под действием управленияи этому переходу соответствует значение функции Беллмана, равное 16 (таблица 1). Переход системы из состоянияв состояниеможет быть выполнен только под действием управления. Поэтому==16.

Таблица 2 - Значения функции Беллмана

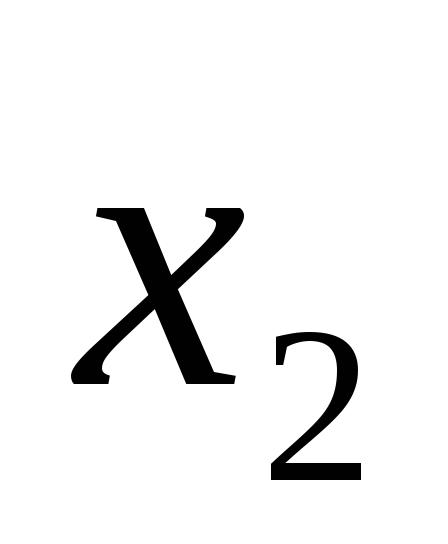
		0	1	2	3	4
0		0	-	-	-	-
		16
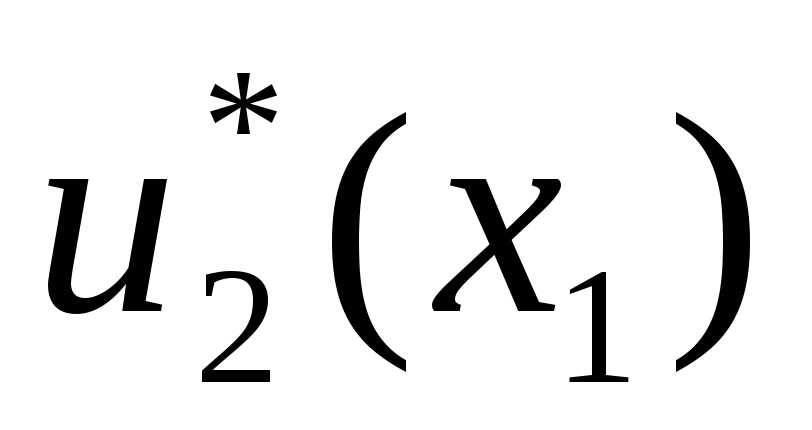
1		1	0	-	-	-
		10	9
2		2	1	0	-	-
		8	5	4
3		3	2	1	0	-
		10	5	2	1
4		4	3	2	1	0
		16	9	4	1	0

Шаг 3 . Используя результаты предыдущего шага, из условия (7) находим условно оптимальное управление и функцию Беллмана=- таблица 3. Прочерки в таблице соответствуют не допустимым управлениям; значения управления и функции Беллмана, выделенные жирным, соответствует оптимальной траектории.

Таблица 3 - Значения функции Беллмана

		0
0		0
		16
1		1
		10
2		2
		8
3		3
		10
4		4
		16

Рассмотрим, для примера, схему получения значений ,, соответствующих переходу системы из состоянияв состояние. Из состояниясистема может перейти оптимально в состояниеили в состояниеПервому переходу соответствует оптимальное управление, второму переходу – оптимальное управление. Указанным переходам соответствует значение функции Беллмана, равное 16 (таблица 1). Переход системы из состоянияв состояниеможет быть выполнен только под действием управления. Поэтому==16.