§7. Приближенное решение задач оптимального управления методом динамического программирования Беллмана

Рассмотрим (только для простоты записи) задачу оптимального управления для стационарной динамической системы и критерием оптимальности, зависящим только от вектора управления:

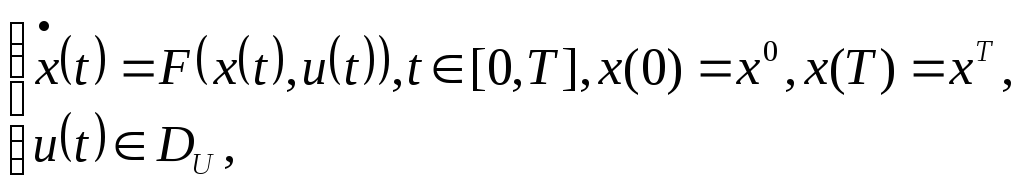(1)

(2)

Обратим внимание на то, что, в отличие от того, как это делалось ранее, для обозначения фазового вектора использована маленькая букваx, а для обозначения вектора управления – маленькая букваu.

Покроем интервал сеткойс шагом(рисунок 1).

Рисунок 1 - Равномерная временная сетка на интервале

Систему ОДУ (1) заменим ее конечно-разностным аналогом

, (3)

а функционал (2) заменим его приближенным значением, вычисленным по формуле прямоугольников

, (4)

где есть-матрица.

Таким образом, задача оптимального управления (1), (2) в дискретной форме имеет вид (3), (4).

Аналогично матрице введем в рассмотрение-матрицуи сформулируем принцип оптимальности (см. параграф 6) для задачи (3), (4).

Утверждение 1 (принцип оптимальности для дискретной системы). Пусть =- оптимальное управление для задачи оптимального управления (3), (4) и пусть=- соответствующая оптимальная фазовая траектория. Тогда для любыхуправлениеи соответствующая траекториябудут оптимальными на интервале времени●

Другими словами, если траектория оптимальна, то и любая ее завершающая часть, начинающаяся из точки, будет оптимальной на последнихшагах. А всякая другая траектория из того же состояния, вообще говоря, не является оптимальной на этих шагах (рисунок 2).

Рисунок 2 - К принципу оптимальности для дискретной системы.

Обозначим значение функционала (4) на завершающих шагах

, .

Тогда если на завершающих шагах управление оптимально, имеет место равенство

=, (5)

где -функция Беллмана последних шагов для дискретной задачи оптимального управления (3), (4).

Из утверждения 1 следует, что на последнем шаге (когда )

=. (6)

Найдем рекуррентное соотношение, связывающее между собой функции ,. Положим для этого, что функцияизвестна. Тогда если наk-ом шаге с начальным состоянием выбрать управление, то процесс перейдет в состояние(начальное для последующихшагов). Если этот переход оптимален, то опять же из утверждения 1 следует искомое соотношение

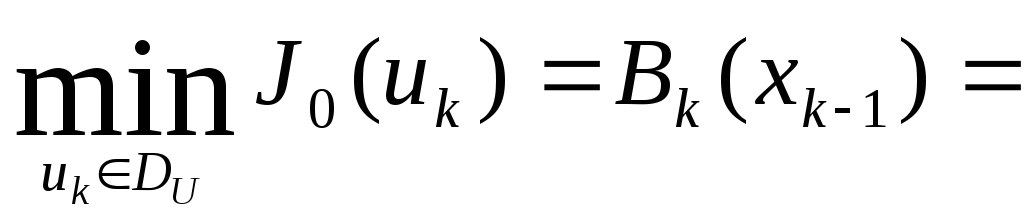
. (7)

Уравнения (6), (7) позволяют последовательно найти функции ,,…,и называютсяуравнениями Беллмана для дискретной системы (3), (4). Отметим, что одновременно с нахождением функций ,,…,оказываются определенными и управления. Поскольку управлениезависит от состояния, это управление называетсяусловно оптимальным управлением.

После нахождения условно оптимальных управлений можно найти искомые управленияпо следующей схеме:

• поскольку состояние известно, находим управление; с этим управлением по формуле (3) находим состояние;

• поскольку состояние известно, находим управление; с этим управлением по формуле (3) находим состояние;

• ……

• поскольку состояние известно, находим управление; очевидно, что=.

Схема приближенного решения задач оптимального управления методом динамического программирования Беллмана

Этап 1

1. Шаг 1. Из условия (6) находим условно оптимальное управление и функцию Беллмана.

2. Шаг 2. Используя результаты предыдущего шага, из условия (7) находим условно оптимальное управление и функцию Беллмана.

3. …………………..

4. Шаг N. Используя результаты предыдущего шага, из условия (7) находим условно оптимальное управление и функцию Беллмана.