§6. Метод динамического программирования Беллмана

Идею метода динамического программирования Беллмана рассмотрим на примере задачи оптимального быстродействия

(1)

(2)

Гипотеза 1. Какова бы ни была отличная от допустимая точка фазового пространства, существует оптимальная (в смысле быстродействия) траектория перехода динамической системы из точкиХ в точку (рисунок 1)●

Рисунок 1 - К гипотезе 1 ()

Время, в течение которого осуществляется оптимальный переход из точки Х в точку , обозначим.

В этих терминах гипотеза 1 может быть сформулирована следующим образом. Для любой точки существует такое управление, под действием которого динамическая система (1) переходит за время, равное, из точкиХ в точку , но за время, меньшее, чем, перейти из точкиХ в точку невозможно.

Гипотеза 2. Функция непрерывна и всюду, кроме, быть может, точки, имеет непрерывные частные производные

●

Пусть теперь - оптимальный процесс перехода системы (1) из состоянияв состояниеи- отрезок времени, в течение которого этот переход происходит;. Другими словами, положим, что

Утверждение 1 (принцип оптимальности). Если процесс оптимален, то процесстакже оптимален.

Доказательство (рисунок 2). Движение по рассматриваемой оптимальной траектории от точки до точкиосуществляется за время, а движение из точкидо точки- в течение времени. Поскольку, быстрее, чем за это время из точкипопасть в точкуневозможно.

Рисунок 2 - К утверждению 1

Действительно, если бы такое движение существовало (пунктир на рисунке 2), то переместившись из точки в точкуза время, а затем из точкив точкубыстрее, чем за время, мы осуществили бы переход извза время, меньшее, чем, что противоречит предположению об оптимальности процесса●

Утверждение 2. Если процесс оптимален, то справедливо уравнение

, (3)

где функция называетсяфункцией Беллмана.

Доказательство. Из принципа оптимальности следует, что есть время оптимального движения из точкив точку, т.е.

. (4)

Заменив в формуле (4) Т на , получим

или

. (5)

Переходя в формуле (5) к пределу при , получим, что на оптимальной траектории выполняется равенство

. (6)

По правилам дифференцирования сложной функции с учетом уравнения (1) из равенства (6) имеем

. (7)

Из принципа оптимальности следует, что соотношение (7) верно для любых . Таким образом, окончательно имеем уравнение (3)

Аналогично утверждению 2 можно доказать справедливость следующего утверждения.

Утверждение 3. Если процесс оптимален, то справедливоуравнение динамического программирования Беллмана

● (8)

Методом динамического программирования Беллмана называется метод решения задач оптимального управления, использующий принцип оптимальности или уравнение динамического программирования Беллмана.

Подчеркнем следующие обстоятельства:

• уравнение динамического программирования Беллмана дает необходимое условие минимума;

• уравнение динамического программирования Беллмана требует выполнения гипотезы 2 относительно неизвестной функции Беллмана 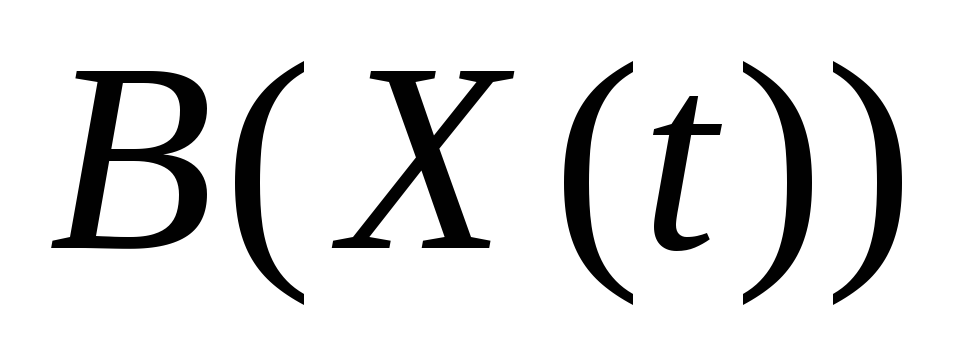. Однако, даже в простейших задачах оптимального управления функцияоказывается не всюду дифференцируемой. По этой причине при решении задач оптимального управления методом динамического программирования уравнение (8) в явном виде не используется - используется принцип оптимальности.

Входные термины:

• задача оптимального управления;

• стационарная динамическая система;

• критерий оптимальности управления;

• вектор фазовых координат динамической системы;

• фазовая траектория динамической системы;

• принцип оптимальности;

• метод динамического программирования Беллмана.

Выходные термины:

• принцип оптимальности для дискретной системы;

• функция Беллмана для дискретной системы;

• уравнения Беллмана для дискретной системы;

• условно оптимальное управление.