§3. Метод приближенного решения задачи оптимального управления, использующий п-систему

Рассмотрим задачу оптимального управления стационарной динамической системой

(1)

(2)

Напомним, что выражения (1), (2) совместно с выражением для соответствующего гамильтониана

_, (3)

сопряженной системой ОДУ для вспомогательной вектор-функции

(4)

и условием максимума

₍₅₎

образуют П-систему задачи оптимального управления (1), (2).

Наиболее точные и аккуратные методы численного решения задач оптимального управления связаны с решением соответствующих П- систем.

Положим, что уравнение (5) можно разрешить относительно , т.е. найти функцию. Тогда формально П-система (1) – (5) сводится к системеуравнений

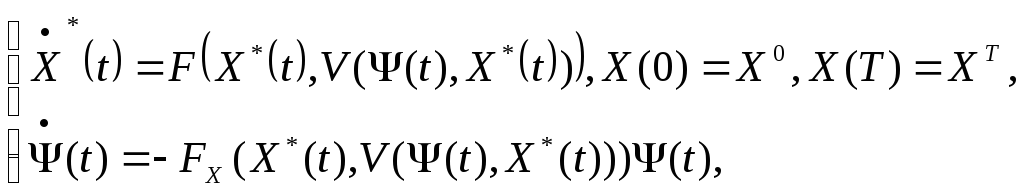(6)

где

Введем в рассмотрение следующую П-процедуру.

1. Задаем некоторые начальные условия для вектор-функции.

2. С заданными начальными условиями ,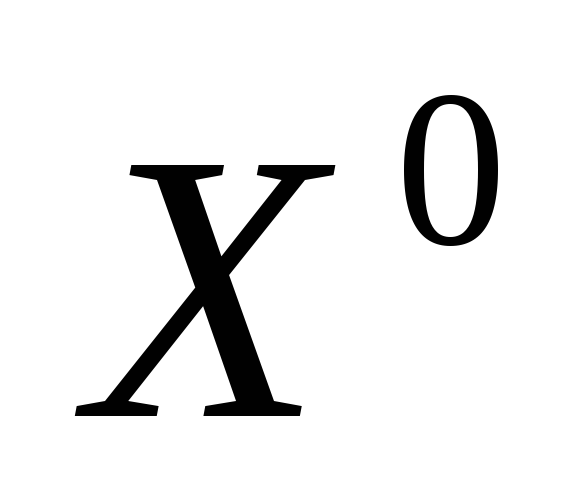решаем задачи Коши (6) – находим функцию,.

3. Находим разность (которая, очевидно, в общем случае не будет равна 0)●

П-процедура устанавливает функциональную зависимость разности от вектора. Обозначим эту функциональную зависимостьZ:

=, (7)

где вектор-функция.

Теперь, формально, решение задачи оптимального управления (1), (2) сводится к решению системы нелинейных алгебраических уравнений (7): найти вектор , при которомили, что тоже самое, при котором .

Чаще всего для решения СНАУ (7) используют метод касательных (метод Ньютона). Напомним схему этого метода для одномерного случая (см. параграф 4.8).

Пусть n=1. Система (7) при этом имеет вид (рисунок 1)

=, (8)

где - соответствующие скалярные константы, а- скалярные функции.

Рисунок 1 - К схеме метода касательных (метода Ньютона). Одномерный случай (n=1)

Линейная функция, аппроксимирующая функцию в точке , записывается в виде

.

Приравняв правую часть этого выражения к нулю, получим итерационную формулу метода касательных

. (9)

В многомерном случае (n>1) итерационная формула (9) имеет вид

, (11)

где - матрица, обратная матрице,

.

Схема метода приближенного решения задачи оптимального управления, использующего П-систему

1. Полагаем счетчик числа итераций .

2. Из каких либо соображений задаем вектор .

3. Выполняем П-процедуру для вектора - вычисляем:

=.

4. Если условие окончание итераций не выполнено (см. ниже), то по формуле (10) вычисляем следующее приближение к , полагаеми переходим к п. 3.

5. В качестве приближения к оптимальному управлению принимаем

●

В качестве условия окончания итераций естественно использовать условие

,

где - некоторая векторная норма, например, евклидова;- требуемая точность выполнения условия=0.

Рассмотрим в заключение основные трудности, возникающие при решении задачи оптимального управления данным методом:

1. Поскольку функция задана неявно, для вычисления - матрицыприходится использовать численное дифференцирование. Для этого на каждой итерации, как минимум, приходитсяраз решать задачи Коши (6).

2. Матрицу на каждой итерации приходится обращать.

3. Метод Ньютона сходится лишь в достаточно малой окрестности решения. Поэтому на практике приходится использовать различные модификации метода Ньютона, обеспечивающие ускорение сходимости.

4. Решение уравнения (8) может быть не единственно.

5. Содержательные соображения для выбора вектора практически отсутствуют. Иногда для выбора этого вектора используют приближенное решение задачи оптимального управления (1), (2) каким-либо другим методом, дающим грубое приближение к.

Входные термины:

• задача оптимального управления;

• динамическая система;

• критерий качества управления.

Выходные термины:

• элементарная операция;

• локальная вариация в фазовом пространстве;

• вариация в фазовом пространстве;

• метод локальных вариаций;

• основной цикл метода локальных вариаций.