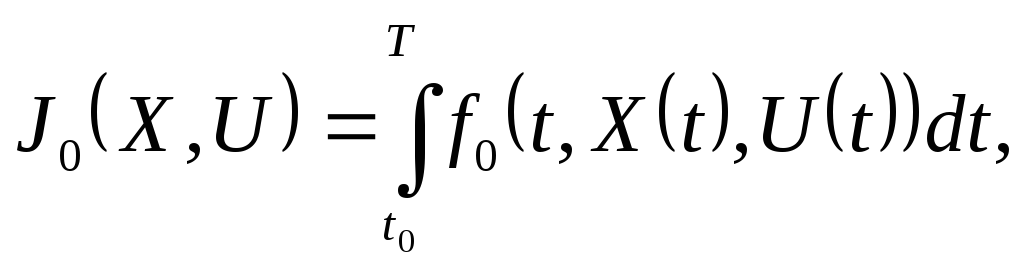Раздел 3

Оптимизация в бесконечномерных пространствах. Задачи оптимального управления и методы их приближенного решения.

Глава 12. Задачи оптимального управления и методы их приближенного решения

Входные термины:

• динамическая система;

• нестационарная динамическая система;

• стационарная динамическая система;

• начальные условия;

• вектор фазовых переменных системы, вектор переменных состояния системы.

Выходные термины:

• задача оптимального управления динамическими системами, задача оптимального управления;

• задача оптимального быстродействия;

• вектор управления;

• множество допустимых значений вектора фазовых переменных системы;

• множество допустимых управлений;

• критерия качества управления динамической системой, критерий оптимальности.

§1. Постановка задачи оптимального управления

Пусть нестационарная динамическая система описывается системой обыкновенных дифференциальных уравнений (ОДУ)

(*)

где - анализируемый период времени (величинаT не обязательно фиксирована!), --вектор начальных условий,--вектор фазовых переменных системы,--вектор управления. В той или иной форме могут быть заданы также условия на конце траектории системы, например, в виде . Заметим, что правильнее было бы последние условия задавать в виде , где- момент достижения системой состояния. Однако для простоты записи мы будем использовать первую запись (если не оговорено противное).

Далее будем использовать описание динамической системы (*) в векторной форме

_,. ₍₁₎

Напомним, что если время t явно не входит в функцию F, то динамическая система, описываемая системой ОДУ (1) называется стационарной.

На вектор в общем случае могут быть наложены ограничения вида

, (2)

где –множество допустимых значений вектора фазовых переменных, – некоторое функциональное пространство, например, пространствонепрерывных на интервалефункций (рисунок 1).

Рисунок 1 - Пример области допустимых значений для одномерной системы (n=1).

На вектор управления также обычно накладываются некоторые ограничения вида

, (3)

где –множество допустимых управлений, – некоторое функциональное пространство, например, пространствофункций «интегрируемых с квадратом» на интервале(рисунок 2).

Используя уравнение (1), формально ограничения на вектор фазовых переменных можно пересчитать в ограничения на вектор управления. Однако, задача такого пересчета сложна и обычно рассматривают и те, и другие ограничения.

В качестве критерия качества управления в задачах оптимального управления обычно используют интегральный функционал вида

(4)

где – некоторая одномерная функция указанных переменных.

Заметим, что здесь и далее обозначение функционала вида (без указания зависимости вектор-функцийот времениt) означает зависимость от этих функций в целом, как элементов соответствующих функциональных пространств. Часто в литературе вместо записив том же смысле используют запись.

Рисунок 2 - Пример множества допустимых управлений для системы с одномерным управлением.. Пространство допустимых управлений, полагается, составляют кусочно-постоянные функции, имеющие на интервалеконечное число разрывов первого рода

Итого, задача оптимального управления динамической системой в достаточно общем виде формализуется следующим образом: найти такой вектор управления , удовлетворяющий условию (3), который на решениях системы ОДУ (1) обеспечивает минимум критерия оптимальности (4) при выполнении ограничений (2) на вектор фазовых переменных.

Возможны и не интегральные формы функционалов качества управления, например:

,

где – некоторое фиксированное время;

Важным частным случаем задачи оптимального управления является задача оптимального быстродействия. Критерий оптимальности получается в этом случае из критерия оптимальности (4) при и имеет вид

.

Пример 1. Тело массой m, находящееся в начальный момент времени в состоянии покоя в точке с координатойx=0, может перемещаться вдоль оси 0x под действием силы тяги двигателя, которым оно снабжено (рисунок 3). Максимальная по величине сила тяги u, которую может развить двигатель, равна a.

При движении тела на него действует сила сопротивления среды F_c, пропорциональная скорости движения тела V, т.е. F_c=-kV, где k – заданный коэффициент пропорциональности.

Расход горючего при работе двигателя пропорционален квадрату развиваемой им силы тяги, т.е. равен γu², где - заданная константа.

Необходимо управлять работой двигателя на промежутке времени таким образом, чтобы при минимальном расходе горючего закон движения тела (т.е. зависимость) как можно меньше отличался от требуемого закона движения.

Рисунок 3 - К примеру 1

Обозначим

.

Таким образом, размерность вектора фазовых переменных системы равна и его можно записать в виде.

По второму закону Ньютона имеем

,

где – ускорение тела.

Итак, движение тела на интервале времени описывает система ОДУ

Так как величина силы тяги в любой момент времени не может превосходить a, имеем место ограничение , т.е. множество допустимых управлений имеет вид

.

Ограничения на вектор фазовых переменных отсутствуют.

Требование постановки задачи о минимальном отличии отможно формализовать различными способами. Обычно используют метрику функционального пространства(гильбертова пространство)

Понятно, что минимуму этого функционала соответствует оптимальный случай.

Кроме того, из постановки задачи следует, что необходимо стремиться к минимуму расхода горючего, т.е. задача является двухкритериальной. Для формализации этого требования введем еще один функционал

Таким образом, в качестве критерия качества управления телом можно использовать функционал

где – весовой коэффициент, учитывающий относительную важность поставленных целей приближенияки экономию горючего●

Входные термины:

• динамическая система;

• нестационарная динамическая система;

• стационарная динамическая система;

• начальные условия;

• вектор фазовых переменных системы, вектор переменных состояния системы;

• задача оптимального управления динамическими системами, задача оптимального управления;

• задача оптимального быстродействия;

• вектор управления;

• множество допустимых значений вектора фазовых переменных системы;

• множество допустимых управлений;

• критерия качества управления динамической системой.

Выходные термины:

• гамильтониан динамической системы;

• сопряженная система ОДУ;

• принцип максимума Л.С.Понтрягина;

• П-система;

• условия трансверсальности;

• задача с подвижными концами;

• динамическая система с параметрами.