5

Работа № 3. Исследование резонансных явлений в линейных электрических цепях

Цель работы – исследование условий возникновения и особенностей проявления резонанса в электрических цепях.

1. Основные положения теории

Резонансом называется режим электрической цепи, при котором собственная частота колебаний участка цепи или всей цепи в целом совпадает с частотой вынужденных колебаний. Различают два вида резонанса: резонанс напряжений и резонанс токов.

0. 1.1 Резонанс напряжений

Резонанс напряжений возникает в цепи, когда ее эквивалентное сопротивление относительно зажимов источника приобретает чисто резистивный характер, при этом реактивные составляющие входного сопротивления взаимно компенсируется. В наиболее простом случае последовательного соединения элементов r,L,C, резонанс возникает при условии, когда, или

где ω₀- резонансная частота контура;- волновое сопротивление контура.

При резонансе Z_ВХ.= r, следовательно,= 0. Ток при резонансе, а так какX_L = X_C, тоU_L0 = U_C0.

Добротность контура Qможет быть определена как

Q = = =

а, следовательно, Qможно определить опытным путем, измеряяU_C0.

При приближении частоты к резонансной напряжения на реактивных элементах резко возрастают. Поэтому такое явление и получило название резонанса напряжений.

Напряжения на индуктивности и емкости достигают максимума на частотах, несколько отличающихся от резонансной. Этот сдвиг зависит от добротности контура и при высокой добротности невелик. Если добротность Q>3, можно условно считать, что максимумыU_CиU_L совпадают с частотой резонанса.

Входное сопротивление контура может быть записано в виде

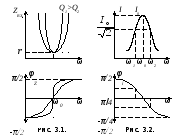
что дает возможность построить амплитудно- и фазочастотную характеристики для Z_ВХ.(рис.3.1). Характер АЧХ и ФЧХ для тока в контуре показан на рис.3.2.

Полоса пропускания – область частот, в которой . Из соотношенияследует, что на границах полосы пропусканияr = ±х,. При таких соотношенияхr и x. Это дает возможность определить частоты на границе полосы пропускания (ω₁,ω₂) по ФЧХ рис.3.2, П = ω₂-ω₁ - абсолютное значение полосы пропускания;S=- относительная полоса пропускания.

Справедливо также соотношение =, гдеd - затухание в контуре.

Граничные частоты могут быть определены по формуле

Избирательностью системы называют ее способность пропускать электрические сигналы в определенной полосе спектра сигналов при существенном подавлении сигналов вне этой полосы. Резонансный контур может выполнять функции избирательной системы.

Избирательность контура при заданной расстройке оценивается в децибелах (дБ) и может быть определена как a= 20lg.

Векторная диаграмма для нагруженного контура при резонансе (рис. 3.3): построение начинаем с параллельного участка - отложим горизонтально вектор токаI_R через сопротивление нагрузки, вектор напряженияU_Rсовпадает по направлению со своим током и равен напряжениюU_C на параллельно включенной емкости, ток через емкостьI_Cопережает свое напряжение на угол/, сумма токовI_CиI_Rравна входному токуI_ВХ., напряжение на индуктивности опережает свой ток, т.е.I_ВХ., на угол/. Проводим прямую линию под прямым углом к векторуI_ВХ., параллельно этой линии проводим пунктир от конца вектораU_Rдо пересечения с векторомI_ВХ., от точки пересечения проводим пунктир параллельноU_Rдо пересечения с прямой линией – получаем параллелограмм, откладываем на диагонали параллелограмма векторU_ВХ., который при резонансе совпадает по направлению сI_ВХ., и векторU_Lна стороне параллелограмма, т.е. «подгоняем» величиныU_ВХ.иU_L.

Для данной схемы напряжение U_C≠U_C0, поэтому напряжениеU_C0находим построением: на перпендикуляре к векторуU_ВХ.находим проекциюU_C . ВеличинуU_C0находим по Пифагору из прямоугольного треугольника. Если величинаU_C значительно превышаетU_ВХ.(более чем в три раза), то единицей под корнем можно пренебречь.

2. Предварительная подготовка

Студенты, пропустившие лаб. работы №1 и №2 и не знающие номер своего стенда, выполняют предварительный расчет для произвольно взятого стенда.

Студенты, записавшиеся на отработку, выполняют предварительный расчет для

произвольно взятого стенда.

Таблица 3.1.

2.1. Для схемы, изображенной на рис.3.4, рассчитать дляR_М= 160 иR_М= 640 Ом : резонансную частотуf₀, добротностиQ, граничные частоты полосы пропусканияf₁ и f₂ , действ. зн. силы тока при резонансеI₀, действ. значения напряжениий на емкости при резонансеU_С0и на границах полосы пропусканияU_С(f₁) и U_С(f₂),R_Ш=100 Ом, активное сопротивление катушки индуктивностиR_LA = 20 Ом, напряжение на генератореU_Г= 2 В.

	ст. № 1	ст. № 2	ст. № 3	ст. № 4	ст. № 5	ст. № 6	ст. № 7	ст. № 8	ст. № 9	ст. № 10
LA , мГн	43,8	45,1	44,9	45,5	46,7	48,1	45,9	45,3	46,3	46,5
CA , мкФ	0,02269	0,02110	0,02338	0,02255	0,02252	0,02155	0,02243	0,02303	0,02393	0,02357

2.2. Рассчитать добротности и резонансные частоты нагруженного контура (рис 3.5) приR_M= 2560 Ом иR_M= 5120 Ом. Записать выражение дляZ _ВХ.(с учетом параллельного соединенияC_A иR_M), выделить мнимую часть и приравнять ее нулю, вычислитьω₀, действительная часть этого выражения равна эквивалентному активному сопротивлению цепиR_ЭКВ.. Вычислить значенияQ =ω₀L_A /R_ЭКВ.. Сделать вывод о влиянии нагрузки на резонансную частоту и добротность. Чему равны добротность и резонансная частота приR_M→ ∞?