TAU_1 / Новая папка / ДЗ 1 ТАУ 12

Методические указания по выполнению

домашнего задания № 1

по дисциплине «ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ»

«Временные характеристики непрерывных линейных

стационарных систем управления»

Цель работы: научиться определять передаточные функции заданной системы, вычислять временные характеристики линейных непрерывных стационарных систем управления с использованием аналитических зависимостей и стандартных функций в пакете MATLAB.

Содержание работы:

1. Определить передаточные функции разомкнутой и замкнутой системы;

2. Записать передаточную функцию замкнутой системы в виде дифференциального уравнения;

3. Определить нули и полюса замкнутой системы;

4. Провести анализ системы во временной области:

Вычислить и построить:

• импульсную переходную функцию (ИПФ) замкнутой системы

• переходную функцию замкнутой системы .

Краткие теоретические сведения

1. Определить передаточные функции разомкнутой и замкнутой системы;

Типовые соединения звеньев

1.Последовательное соединение звеньев:

Передаточная функция последовательного соединения звеньев равна произведению передаточных функций отдельных звеньев.

2. Параллельное соединение звеньев:

Передаточная функция параллельного соединения звеньев равна сумме передаточных функций отдельных элементов.

3. Звено, охваченное обратной связью (рис.1):

Для такой системы справедливы соотношения:

Рис. 1 Соединение с обратной связью

Или , тогда .

Окончательно получим

Передаточная функция замкнутой системы с отрицательной обратной связью (ООС) равна передаточной функции прямой цепи, делённой на 1 плюс произведение передаточной функции прямой цепи на передаточную функцию обратной цепи.

Замкнутую систему называют одноконтурной, если при её размыкании в какой-либо точке получается цепочка из последовательно соединенных звеньев или цепь, не содержащая параллельных и обратных связей.

Участок цепи по ходу сигнала от точки приложения входного сигнала до точки съёма выходного сигнала называется прямой цепью и обозначается .

Участок цепи по ходу сигнала от точки приложения входного сигнала до точки размыкания называется разомкнутой цепью и обозначается

Обычно САУ размыкается в обратной цепи перед элементом сравнения по соответствующему воздействию.

В САУ общая (главная) обратная связь, создающая замкнутый контур, всегда отрицательная.

Для одноконтурной системы с отрицательной обратной связью (ООС) справедливо следующее правило:

Передаточная функция одноконтурной системы с ООС равна передаточной функции прямой цепи, делённой на единицу плюс передаточную функцию разомкнутой цепи.

.

Рассмотрим пример.

Пусть задана структурная схема системы (рис. 2).

Рис. 2. Структурная схема системы управления числом оборотов двигателя с математическими моделями в форме передаточных функций

Определим сначала ПФ внутреннего контура, охваченного местной обратной связью. В прямой цепи этого контура располагается последовательно три звена.

ПФ прямой цепи равна произведению ПФ звеньев

.

ПФ обратной цепи .

Эквивалентная ПФ этого участка системы будет иметь вид:

Обозначим

, тогда

.

Теперь найдём ПФ замкнутой САУ:

, где

Подставляя численные значения параметров, получим ПФ в виде:

2. Записать передаточную функцию в виде дифференциального уравнения;

По известной передаточной функции замкнутой САУ получим дифференциальное уравнение этой системы.

.

Тогда .

Переходя в пространство оригиналов, получим

.

3. Определить нули и полюса передаточной функции замкнутой системы.

Значения , при которых ПФ обращается в нуль, называются нулями ПФ. Нули являются корнями уравнения =.

Значения , при которых ПФ обращается в бесконечность, называются полюсами ПФ. Полюсы являются корнями уравнения .

Передаточная функция имеет нулей и полюсов. Нули и полюса могут быть действительными или комплексно-сопряженными, поэтому их можно изобразить на комплексной плоскости (s-плоскости)

ПФ системы

Последнее выражение является дробно-рациональной функцией, причем коэффициенты ПФ — действительные числа.

Найдем нуль системы: .

Найдём корни уравнения .

Корни последнего уравнения: .

4. Провести анализ системы во временной области:

Импульсная переходная характеристика замкнутой системы :

Из определения передаточной функции следует, что .

Пусть входной сигнал представляет собой единичный мгновенный импульс , изображение которого имеет вид .

Изображение выходного сигнала имеет вид:

.

Найдём импульсную переходную функцию системы .

Если изображение является дробно-рациональной функцией

, то

нахождение оригинала можно осуществить по следующим формулам:

1. Корни простые, вещественные:

. (1)

2. Корни комплексно-сопряженные:

, если , где ; (2)

Импульсная переходная функция системы будет равна , где n - число корней характеристического уравнения.

Переходная функция замкнутой системы .

Пусть входной сигнал представляет собой единичную ступенчатую функцию , тогда изображение единичного сигнала имеет вид .

Изображение выходного сигнала имеет вид .

Найдём переходную функцию системы .

1. Корни простые, вещественные и один корень нулевой, т.е. .

. (3)

2. Корни комплексно-сопряженные и один нулевой:

, если , где ; (4)

Рассмотрим пример. Пусть передаточная функция замкнутой системы имеет вид

.

1. Вычисление корней характеристического уравнения

Характеристическое уравнение имеет вид:

.

Решаем исходное уравнение и находим корня уравнения:

; ; .

Импульcная переходная функция (ИПФ) системы:

Для вещественного корня характеристического уравнения системы используем формулу (1).

1.Определим .

2. Рассчитаем составляющую импульсной переходной функции: .

Обозначим , тогда

Для пары комплексно-сопряженных корней характеристического уравнения системы используем формулу (2).

.

Рис. 3. График импульсной переходной характеристики системы

Определим начальное и конечное значение функции, используя теоремы о начальном и конечном значении.

- теорема о начальном значении

- теорема о конечном значении.

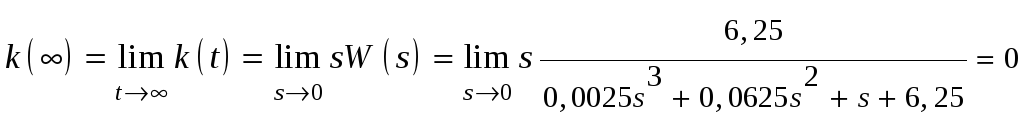
Переходная характеристика замкнутой системы:

Пусть входной сигнал представляет собой единичную функцию . Изображение единичного входного сигнала имеет вид . Тогда изображение выходного сигнала примет вид

Корни характеристического уравнения единичной кратности:

; ; , .

Для расчёта переходной функции используем формулу (3) и (4):

.

График переходной характеристики замкнутой системы показан на рис. 4

Рис. 4. График переходной характеристики системы

Определим начальное и конечное значение функции.

;

.

Домашнее задание должно содержать:

1. Передаточные функции разомкнутой и замкнутой системы, полученные самостоятельно и при помощи стандартных функций MATLAB;

2. Дифференциальное уравнение полученной замкнутой системы;

3. Нули и полюса замкнутой системы;

3. Аналитический расчёт импульсной переходной и переходной функций;

4. Начальные и конечные значения временных функций и ;

5. Графики и , полученные расчётным путём и при помощи стандартных функций пакета MATLAB. Сравнить полученные результаты.

8