TAU_1 / Новая папка / Преоб. Лапласа ТАУ 12

Преобразование Лапласа.

Пусть задана функция вещественного переменного , определённая при . Функция, которая подвергается преобразованию Лапласа, должна обладать следующими свойствами:

1. функция должна быть определена и дифференцируема по всей положительной полуоси ;

2. функция должна быть тождественно равна 0 при , т.е. ( при );

3. функция должна быть ограниченна, т.е. для функции существуют такие положительные числа М и с, что при , т.е. , где с – абсцисса абсолютной сходимости (некоторое положительное число).

Т.о. для некоторой кусочно-непрерывной функции , возрастающей при не быстрее чем , может быть поставлено в соответствие её преобразование Лапласа.

Преобразованием Лапласа называют соотношение вида ,

ставящее функции вещественного переменного в соответствие функцию комплексного переменного ().

При этом называется оригиналом, – изображением, для обозначения соответствия между изображением и оригиналом используют знак соответствия «».

Используется также символическая запись преобразования Лапласа, а именно,

, где – оператор прямого преобразования Лапласа.

- образ функции является функцией комплексного переменного , определяемой при .

Если функция тождественно равна 0 при , то может быть однозначно определена (с точностью до значений в точках разрыва) по своему - образу, т.е. , где - оператор обратного преобразования Лапласа.

Рассмотрим несколько примеров:

1.

;

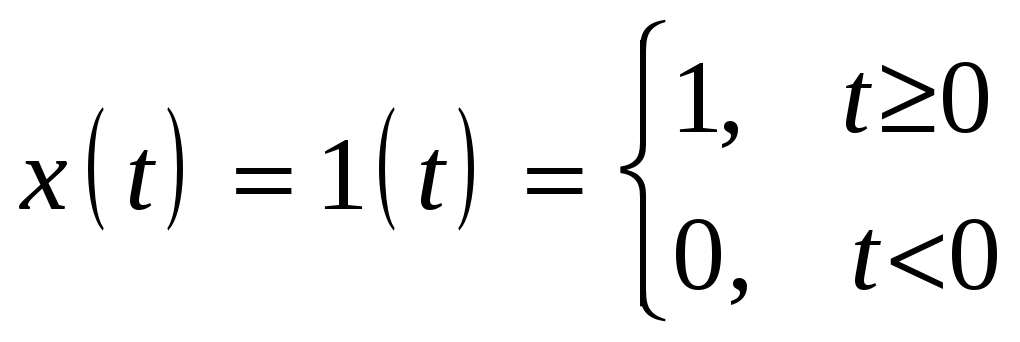
2.

3.

Преобразование Лапласа обладает следующими свойствами:

• Линейности:

если , то , где

• Изменения масштаба во временной области:

если то .

• Смещения аргумента в области изображения (комплексной области):

пусть , тогда

• Смещения аргумента в области оригинала (вещественной области):

пусть , тогда

• Дифференцирования оригинала:

при ненулевых начальных условиях

при нулевых начальных условиях .

• Интегрирования оригинала при нулевых начальных условиях:

.

• Свертки функций в действительной области:

• О предельных значениях:

- теорема о начальном значении

- теорема о конечном значении.

Приведённые свойства преобразования Лапласа позволяют существенно упростить решение дифференциальных уравнений, т.е. cвести решение ДУ к проведению простейших алгебраических операций.

Передаточная функция в преобразованиях Лапласа

Вернёмся к записи дифференциального уравнения в виде (1)

Эту запись можно использовать в компактной форме

.

Пусть функции и являются непрерывными, дифференцируемыми, ограниченными и тождественно равными 0 при .

Применим преобразование Лапласа при нулевых начальных условиях к (1):

Обозначим: ,

.

Запишем полученное выражение в компактной форме

, где

- обычные функции комплексного переменного.

Изображение выходного сигнала системы , т.е. изображение выходного сигнала равно изображению входного сигнала, умноженному на комплексную передаточную функцию системы.

Дадим одно из ключевых в теории автоматического управления определений: Комплексной передаточной функцией (ПФ) системы называется отношение изображения по Лапласу выходного сигнала к изображению по Лапласа входного сигнала при нулевых начальных условиях.

Формально комплексная передаточная функция может быть получена из дифференциального уравнения после замены в нем символа кратного дифференцирования на соответствующую степень и деления многочлена правой части уравнения на многочлен левой части.

Рассмотрим пример: .

Проведём преобразования Лапласа при нулевых начальных условиях:

.

Передаточная функция представляет собой дробно-рациональную функцию, причем в реальной системе порядок числителя не превышает порядка знаменателя , т.е. . Коэффициенты передаточной функции вещественны, поскольку они представляют собой функции от вещественных параметров системы.

Значения , при которых ПФ обращается в нуль, называются нулями ПФ. Нули являются корнями уравнения

.

Значения , при которых ПФ обращается в бесконечность, называются полюсами ПФ. Полюсы являются корнями уравнения

.

Передаточная функция имеет нулей и полюсов. Как нули, так и полюса могут быть действительными или комплексно-сопряженными.

Нули и полюса называются левыми (правыми), если они расположены в левой (правой) части s-плоскости, и нейтральными или нулевыми, если они лежат соответственно на мнимой оси или в начале координат.

Нахождение оригиналов функций по их изображениям

Вычисление оригинала функции по её изображению можно проводить несколькими способами:

1 способ - табличный

При невысоком порядке системы удобно использовать для вычисления оригиналов и изображений стандартную таблицу типовых функций и их изображений.

ТАБЛИЦА ИЗОБРАЖЕНИЙ ТИПОВЫХ ФУНКЦИЙ

Вещественные корни		Комплексно-сопряжённые корни
ОРИГИНАЛ	ИЗОБРАЖЕНИЕ	ОРИГИНАЛ	ИЗОБРАЖЕНИЕ

2 способ - комбинированный.

Разложение передаточной функции системы на простые дроби методом неопределённых коэффициентов и использование таблицы типовых функций и их изображений для вычисления оригинала функции.

Если правильная рациональная дробь, то можно представить в виде произведения линейных и квадратичных сомножителей с действительными коэффициентами.

Корни:

• нулевые () - ; нулевые кратные ;

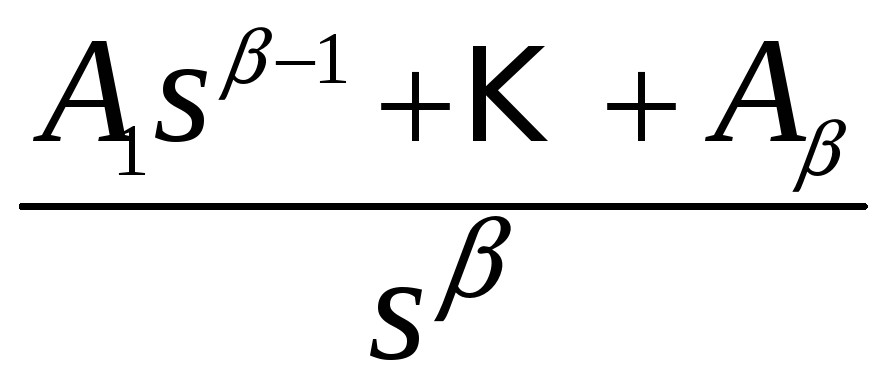• действительные (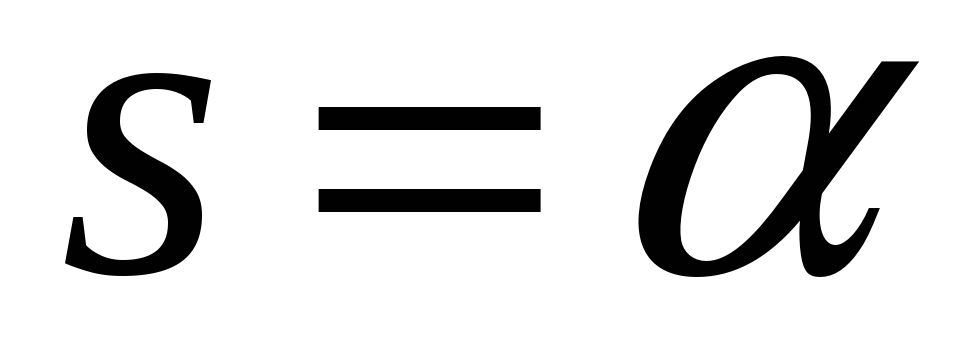) - ; действительные кратные ;

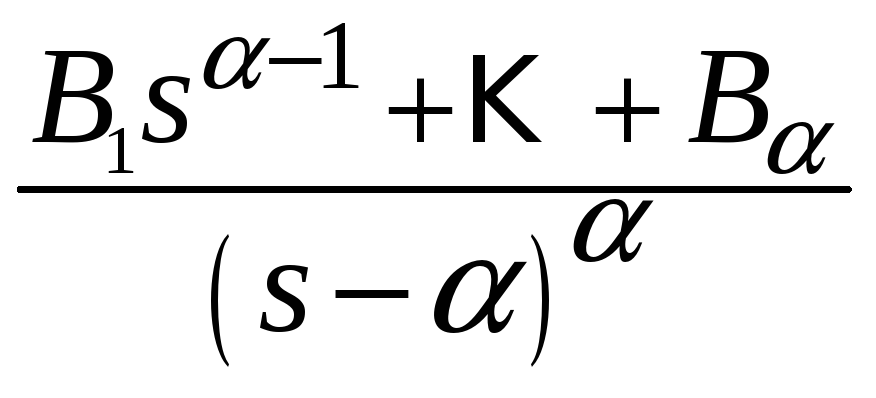• чисто мнимые () - ;

• комплексно-сопряжённые () - ;

,

где и полиномы, соответствующие кратности знаменателя.

Записав в виде суммы дробей, приводят их к общему знаменателю и приравнивают многочлены числителя правой и левой части, определяют коэффициенты и по таблице оригиналов и изображений получают окончательный результат.

3 способ - аналитический

Порядок вычисления оригинала функции по его изображению:

1. Вычислить корни полинома : .

Число корней равно порядку полинома .

2. Выбрать метод определения оригинала (табличный, аналитический, комбинированный).

3. Вычислить производную .

4. Вычислить значения полиномов и при подстановке корней полинома .

5. Вычислить значения коэффициентов при функциях .

Если изображение функции является дробно-рациональной функцией вида

, то

нахождение оригиналов можно осуществить по следующим формулам:

1. Корни простые, вещественные:

.

Пример 1. Определить оригинал функции, если его изображение имеет вид:

.

1. .

2. Корни вещественные.

3. Вычисляем .

.

2 Корни простые, вещественные и один корень нулевой, т.е. .

.

Пример 2. Определить оригинал функции, если его изображение имеет вид:

1. .

2. Корни вещественные и один нулевой

3. Вычисляем .

.

Проверим правильность полученного результата, используя комбинированный метод. Разложим изображение на простые сомножители, определим коэффициенты и по таблице определим оригинал, соответствующий каждой простой дроби.

.

3. Корни комплексно-сопряженные: (считается для одного корня)

, если

Пример 3. Определить оригинал функции, если его изображение имеет вид:

.

1. .

2. Корни комплексно-сопряжённые

3. Вычисляем

4. Расчёт для одного корня: .

Проверим полученный результат, для этого приведём изображение к виду, соответствующему изображениям таблицы типовых функций (стр.4).

4. Корни комплексно-сопряженные и один нулевой:

;

Пример 4. Определить оригинал функции, если его изображение имеет вид:

.

1. .

2. Корни комплексно-сопряжённые и один нулевой

3. Вычисляем

4. Расчёт для одного корня: .

Проверим правильность полученного результата, используя комбинированный метод. Разложим изображение на простые сомножители, определим коэффициенты и по таблице определим оригинал, соответствующий каждой простой дроби.

5. Корни кратные:

.

Пример 5. Определить оригинал функции, если его изображение имеет вид:

Определим корни системы: . Корень является кратным, его кратность равна . Система имеет три корня, поэтому оригинал функции должен содержать три составляющие.

Определим составляющую от вещественного корня, используя формулу (1).

Определим составляющие оригинала для кратного корня

Окончательно имеем

.

Проверить полученный результат можно с использованием комбинированного метода путём разложения на простейшие дроби.

8