
TAU_1 / Новая папка / Моделировние систем управления с помощью МАТЛАВ
.pdf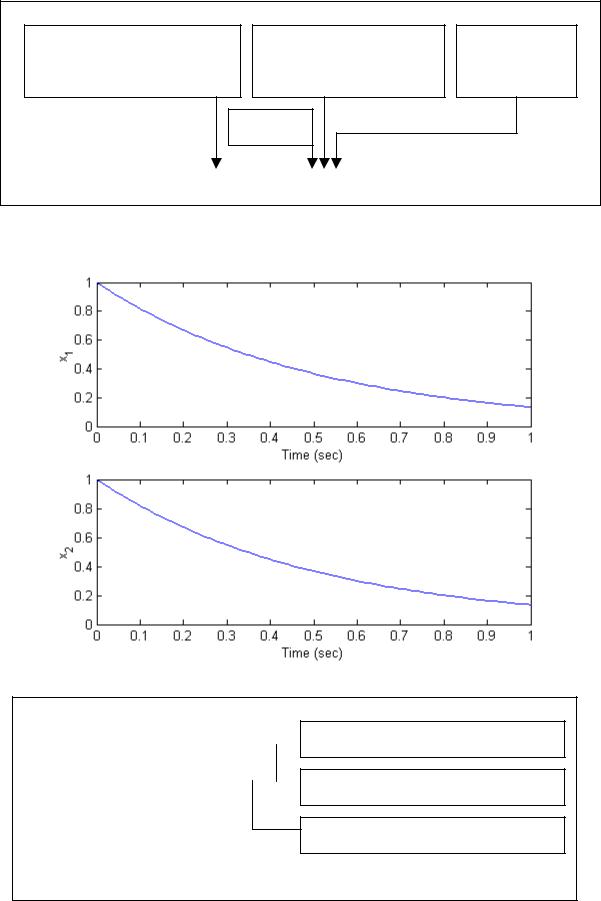
y – выход в момент t |
t – моменты времени, |
Начальные |
T: – вектор состояния |
в которые вычисляется |
условия |
x(t) – состояние в момент t |
реакция |
(по выбору) |
|
u =вход |
|
[y,T,x]=lsim(sys,u,t,x0) |
|
|
Рис. 3.5 Функция lsim для вычисления состояния и выходной переменной |
||
>>A=[0 -2;1 -3]; B=[2;0]; C=[1 0]; D=[0];
>>sys=ss(A,B,C,D);
>>x0=[1 1];
>>t=[0:0.01:1];
>>u=0*t; 

>>[y,T,x]=lsim(sys,u,t,x0);
>>subplot(211), plot(T,x(:,1))
>>xlabel('Time (sec)'), ylabel('x_1')
>>subplot(212), plot(T,x(:,2))
>>xlabel('Time (sec)'), ylabel('x_2')
Модель в переменных состояния
Начальные условия
Нулевой входной сигнал
Рис. 3.6. Вычисление с помощью функции lsim временных характеристик при ненулевых начальных условиях и отсутствии входного сигнала
41
4. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Рассмотрите два полинома:
p(s) = s2 + 2s+1, q(s) = s+1.
Спомощью MATLAB вычислите следующие:
a)p(s)q(s)
б) полюсы и нули G(s)= qp((ss))
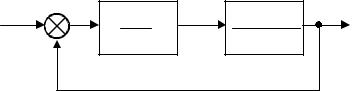
2. Рассмотрите систему с обратной связью, изображенную на рис. 3.1
|
|
Регулятор |
Объект |
Y (s) |
+ |
1 |
X (s) |
|
|
s+ 2 |
|
|
− |
s+1 |
s+3 |
Рис .3.1 Система с отрицательной обратной связью |
|||
а) Вычислите передаточную функцию замкнутой системы с помощью функций
MATLAB series и feedback.
б) Определите реакцию системы на единичное ступенчатое воздействие с помощью функции step и убедитесь, что конечное значение выходной переменной равно 2/5.
3. Дано дифференциальное уравнение x+ 4x+ 4x = y, где x(0)= x(0)= 0 и y(t) есть единичная ступенчатая функция. Получите решение этого уравне-
ния аналитически и проверьте результат с помощью MATLAB, одновременно построив график x(t) с помощью функции step.
4. Система управления положением спутника по одной координате может быть представлена структурной схемой, изображенной на рис. 3.2. Переменные k, a иb являются параметрами регулятора, а J есть момент инерции спутника.
Примите следующие значения J =10,8E + 08, k =10,8E + 08, a =1иb =8.
42
Модель
вращения Регулятор спутника
θ |
d |
(t) |
+ |
k(s+ a) |
1 |
θ(t) |
|
|
|
|
|||
Заданное |
− |
s+b |
Js2 |
Действительное |
||
положение |
|
|
|
положение |
||
Рис. 3.2 Структурная схема системы управления положением спутника по одной координате
а) Напишите программу MATLAB, вычисляющую передаточную функцию замкнутой системы W (s)= θ(s) θd (s).
θd (s).
б) Вычислите и постройте график реакции системы на ступенчатое изменение
входного сигнала величиной 10o.
в) Точное значение момента инерции спутника в общем случае неизвестно и может медленно изменяться во времени. Сравните реакции системы в случаях, когда J уменьшается на 20% и на 50%. Параметры регулятора при этом остаются неизменными. Проанализируйте полученные результаты.
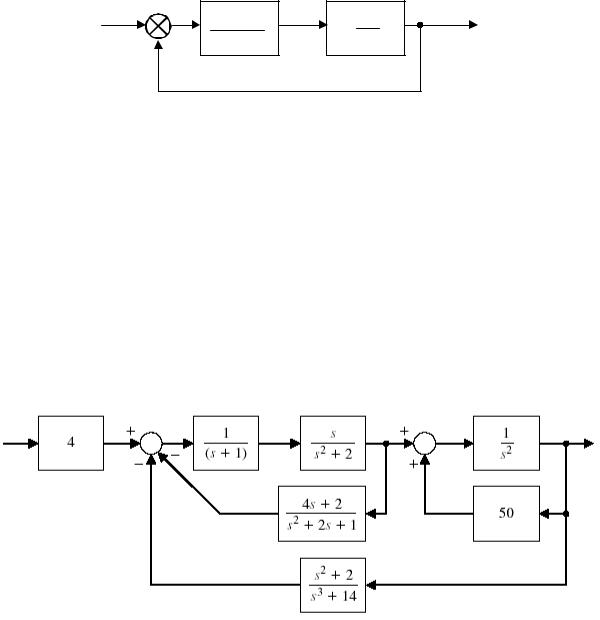
5. Рассмотрите структурную схему системы, представленную на рис. 3.3.
Y (s) |
X (s) |
Рис. 3.3 Структурная схема многоконтурной системы управления
а) С помощью MATLAB упростите структурную схему системы и определите передаточную функцию замкнутой системы.
б) С помощью функции pzmap определите положение полюсов и нулей передаточной функции замкнутой системы.
в) С помощью функций pole и zero вычислите точные значения полюсов и нулей передаточной функции замкнутой системы и сравните с результатами с данными, полученными в п.б).
6. Связь между выходом y(t) и входом x(t) нелинейной системы определяется уравнением
43

y(x) = x2 + xsinx.
Линейная аппроксимация этой зависимости имеет вид: y = ax,
где a – коэффициент подлежащий определению. Определите параметр a экспериментально, разработав программу MATLAB, которая вычисляет и строит график разности между y и y в зависимости от переменного параметра a. Па-
раметр a подбирайте та, чтобы максимальная разность между y и y не пре-
вышала значения 20 при 0≤ x ≤10. Когда будет найдено соответствующие значение a, построите графики y и y в диапазоне 0≤ x ≤10.
7. Система имеет передаточную функцию
X((s)) = (15 z)(s + z)
z)(s + z)
Y s s2 +3s+15
Постройте график реакции системы на сигнал y(t) в виде единичной функции при значениях параметра z =3, 6 и 12.
8. С помощью функции ss получите модель в переменных состояния для систем, имеющих в разомкнутом состоянии следующие передаточные функции:
а) W (s)= |
1 |
, б) W (s)= |
3s2 +10s+1 |
, в) W (s)= |
s+14 |
. |
|||
|
|
|
|
|
|||||
s+10 |
s2 +8s+ 5 |
|
s3 +3s2 + 3s+1 |
||||||
|
|
|
|
||||||
9. С помощью функции tf определите передаточные функции для систем, модели которых в переменных состояния представлены следующими матрицами:
а) A = |
0 |
1 |
|
|
1 |
|
||
|
|
,B = |
,C=[1 0]; |
|||||
|
2 |
4 |
|
|
1 |
|
||
|
|
1 |
1 |
|
0 |
|
|
0 |
б) A = −2 |
0 |
|
4 |
,B = 0 ,C=[0 1 0]; |
||||
|
|
6 |
2 |
|
|
|
|
|
|
|
10 |
|
1 |
||||
в) A = |
|
0 |
1 |
|
,B |
0 |
,C=[1 1]. |
|
|
−1 |
|
|
= |
||||
|
|
−2 |
|
|
1 |
|
||
10. Рассмотрите систему, заданную уравнениями
44
|
0 |
1 |
0 |
0 |
X = 0 |
0 |
1 X+ |
0 u, y =[1 0 0]X. |
|
|
−3 |
−2 |
|
|
|
−5 |
1 |
||
а) С помощью функции tf определите передаточную функцию Y(s) U(s).
U(s).
б) Постройте график реакции системы на начальные условия X(0)=[0 −1 1]T
для 0≤ t ≤10.
в) С помощью функции expm вычислите переходную матрицу состояния и определите X(t) при t =10 для начальных условий из п. (б). Сравните получен-
ные результат с данными их п. (б).
11. Рассмотрите две системы:
|
|
0 |
1 |
0 |
|
|
|
0 |
|
X |
= |
0 |
0 |
1 |
X |
+ 0 u, y =[1 0 0]X |
|||
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
−4 |
5 |
|
|
|
|
|
|
|
|
−8 |
|
|
4 |
|
|||
и
|
0,5 |
0,5 |
0,7071 |
|
0 |
|
X2 = |
−0,5 |
−0,5 |
0,7071 X2 |
+ 0 u, y =[0,7071 −0,7071 0]X2. |
||
|
|
0,7071 |
−8 |
|
|
|
−6,354 |
|
|
4 |
|||
а) С помощью функции tf определите передаточную функцию Y(s) U(s) для
U(s) для
системы (1).
б) Проделайте то же самое для системы (2)
в) Сравните результаты пп. (а) и (б) и прокомментируйте их.
12. Рассмотрите замкнутую систему, представленную на рис. 3.4.
|
|
Регулятор |
Объект |
Y (s) |
+ |
1 |
X (s) |
|
|
1 |
|
|
− |
s+ 2 |
s2 + 2s+ 4 |
|
|
Рис. Замкнутая система управления |
|
а) С помощью MATLAB получите модель в переменных состояния для регулятора.
б) Проделайте то же самое для объекта.
45
в) Используя результаты пп. (а) и (б), с помощью функций series и feedback получите модель в переменных состояния для замкнутой системы и постройте график ее реакции на импульсное входное воздействие.
13. Рассмотрите систему
|
0 |
1 |
0 |
X = |
−2 |
X+ u, y =[1 0]X |
|
|
−3 |
1 |
|
при начальных условиях X(0)=[1 0]T.
С помощью функции isim вычислите и изобразите графически реакцию переменных x1(t) и x2 (t) при u(t) = 0.
ЛИТЕРАТУРА
1.Дьяков В.П., Абраменкова И.В. MATLAB 5.0/5.3. Система символьной математики. М.: Нолидж. – 1999 г. 640 с., ил.
2.Медведев В.С., Потемкин В.Г. Control System Toolbox. MATLAB для сту-
дентов / под общей ред. В.Г. Потемкина – М.: ДИАЛОГ-МИФИ. – 1999. – 287 с.
3.Методы классической и современной теории автоматического управления: Учебник в 3-х т. Т.1: Анализ и статистическая динамика систем автоматического управления / Под ред. Н.Д. Егупова. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. – 748 с.
46
