
TAU_1 / Новая папка / Моделировние систем управления с помощью МАТЛАВ
.pdfМосковский государственный технический университет им. Н.Э. Баумана, Калужский филиал
Ю.Л. Лукашенко, Д.В. Мельников
МОДЕЛИРОВАНИЕ СИСТЕМ УПРАВЛЕНИЯ С ПОМОЩЬЮ
MATLAB
Методические указания по выполнению лабораторных работ по курсу
«Проектирование алгоритмов и программного обеспечения» для студентов специальности
«Системы автоматического управления летательных аппаратов»
Калуга
2003
УДК 681.5:681.3 М 54
Данное руководство издается в соответствии с учебным планом специальности 210500 «Системы управления летательными аппаратами»
Указания рассмотрены и одобрены:
Кафедрой «Системы автоматического управления и электротехники» (ЭИУ3-КФ, КФ МГТУ им. Н.Э. Баумана)
протокол № 5 от 5 марта 2003 г.
Зав. кафедрой ЭИУ3-КФ, |
|
|
д.т.н., профессор |
________________ |
Н.Д. Егупов |
Методической комиссией № _____от____________ 2003 г.
Председатель методической комиссии |
|
|
|
КФ МГТУ им. Н.Э. Баумана, |
|
|
|
к.ф-м.н., доцент |
______________ |
В.И. Дегтярев |
|
Рецензент: |
______________ |
|
Зам. зав. каф. ЭИУ1-КФ, |
|
|
д.т.н., проф., Ю.П. Корнюшин |
|
Авторы: |
______________ |
д.т.н., проф. Ю.Л. Лукашенко, |
|
|
|||
|
______________ |
к.т.н. доц. Д.В. Мельников |
|
АННОТАЦИЯ
В методических указаниях излагаются основы ядра MATLAB, описываются основные функции специализированного пакета прикладных программ Control Systems Toolbox, который позволяет в сочетании с основной программой моделировать системы автоматического управления, описываемых как передаточными функциями, так и в переменных состояния, приводятся задания для самостоятельной работы. Предназначены для студентов специальности 210500 «Системы управления летательными аппаратами».
©Калужский филиал МГТУ им. Н.Э. Баумана, 2003 г.
©Ю.Л. Лукашенко, Д.В. Мельников
|
ОГЛАВЛЕНИЕ |
|
1. |
Основы MATLAB |
4 |
2. |
Моделирование систем управления описываемых |
|
|
передаточными функциями |
21 |
3. |
Моделирование систем управления описываемых |
|
|
в переменных состояния |
37 |
4. |
Задания для самостоятельной работы |
42 |
Литература |
46 |
|

1 ОСНОВЫ MATLAB
Введение
MATLAB – это интерактивная среда для научных и инженерных вычислений. В состав MATLAB входят основная программа (ядро) и специализированные пакеты прикладных программ (toolboxes), состоящие из так называемых М-файлов, расширяющих функциональные возможности основной программы. Один из таких пакетов, Control Systems Toolbox, в сочетании с основной программой дает возможность использовать MATLAB для анализа и синтеза систем управления.
Независимо от того, к какой платформе принадлежит компьютер, или какая операционная система используется, большинство инструкций, функций и команд MATLAB применяются совершенно одинаково. Обычно при работе в среде MATLAB пользователь взаимодействует с компьютером с помощью четырех основных объектов:
1.инструкции и переменные;
2.матрицы;
3.графические изображения;
4.скрипты.
MATLAB интерпретирует и обрабатывает входные данные в виде одного или нескольких этих объектов. Цель данного раздела – рассмотреть каждый из перечисленных объектов, чтобы студент получил начальную подготовку по решению в среде MATLAB задач анализа и синтеза систем автоматического управления.
Инструкции и переменные
Инструкции имеют общий вид, приведенный на рис. 1.1. В MATLAB используется операция присваивания, так что знак равенства «=» означает, что некоторой переменной присваивается выражение справа от этого знака.
Командная строка обозначается двумя направленными вправо стрелками «>>». Пример инструкции приведен на рис. 1.2, где производится ввод матрицы размера 2×2 и ей присваивается имя переменной А. Инструкция выполняется после возврата каретки (нажатие клавиши <enter>). Во всех остальных примерах нажатие этой клавиши подразумевается по умолчанию.
|
|
|
|
>>А=[1 2; 4 6] <ret> |
|
|
||
|
|
Курсор |
|
|
|
|||
|
|
|
A= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
Возврат |
|
||
|
|
|
|
4 |
6 |
|
|
|
|
>>переменная = выражение |
|
|
каретки |
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Рис. 1.1. Форма записи инструкции в |
Рис. 1.2. Ввод и отображение матрицы А |
|||||||
|
MATLAB |
|
|
|
|
|
||
|
|
|
|
4 |
|
|
|
|

После ввода инструкции, завершающегося нажатием клавиши <enter>, матрица А автоматически отображается на экране. Если после инструкции следует точка с запятой (;), то вывод матрицы А на экран подавляется, как показано на рис. 1.3. Тем не менее, присвоение матрице имени А сохраняется, хотя ее вывод на экран подавлен точкой с запятой. При работе с MATLAB будут часто встречаться случаи, когда производятся какие-то промежуточные вычисления, вывод результатов которых на экран не представляет интереса. Поэтому всегда, когда желательно уменьшить количество выводимых данных, необходимо использовать символ точки с запятой. Это также позволяет ускорить решение задачи, т.к. вывод данных на экран требует определенного времени.
В выражениях могут быть использованы обычные символы математических операций, приведенные в табл. 1.1. Порядок выполнения арифметических действий можно изменить с помощью скобок.
|
|
|
|
|
|
|
>> A=[1 2;4 6]; |
|
|
Точка с запятой |
|
|
|
|
|
запрещает вывод |
|
|
||
>> |
|
|
|
|
|
|
|
|
|
|
|
|
|
>> A=[1 2;4 6] |
|
|
|
|
|
|
|
|
|
|
|
||
A = |
|
|
|
|
|
|
1 |
2 |
|
Отсутствие точки с запятой |
|
||
4 |
6 |
|
|
разрешает вывод |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.3. Использование точки с запятой для подавления вывода
Таблица 1.1. Символы математических операций
+ |
Сложение |
- |
Вычитание |
* |
Умножение |
/ |
Деление |
^ |
Возведение в степень |
Если в выражении отсутствуют имя переменной и символ «=», то результату автоматически присваивается имя ans. В MATLAB доступно большинство тригонометрических и элементарных математических функций. Полный перечень этих функций можно найти в руководствах для пользователей MATLAB, а наиболее часто встречающиеся из них приведены в табл. 1.2. Имена переменных должны начинаться с буквы, за которой может быть следовать любое количество букв и цифр (включая символ подчеркивания). Старайтесь, чтобы имя переменной было ограничено 19 символами, т.к. MATLAB запоминает только первые 19 символов. Всегда желательно, чтобы имя переменной отражало смысл той величины, которую она представляет. Например, для переменной, которая представляет скорость самолета (aircraft velocity), можно было использовать имя vel. Обычно не рекомендуется использовать очень длинные имена переменных, хотя MATLAB это и допускает. MATLAB различает верхний и нижний регистры.
5

Таблица 1.2. Распространенные математические функции
sin(x) |
Синус |
acoth(x) |
Гиперболический арккотангенс |
|
sinh(x) |
Гиперболический синус |
exp(x) |
Экспоненциальная функция |
|
asin(x) |
Арксинус |
log(x) |
Натуральный логарифм |
|
asinh(x) |
Гиперболический арксинус |
log10(x) |
Десятичный логарифм |
|
cos(x) |
Косинус |
log2(x) |
Логарифм по основанию 2 |
|
cosh(x) |
Гиперболический косинус |
pow2(x) |
Степень числа 2 |
|
acos(x) |
Арккосинус |
sqrt(x) |
Квадратный кроень |
|
acosh(x) |
Гиперболический косинус |
nextpow2(x) |
Ближайшая степень числа 2 |
|
tan(x) |
Тангенс |
abs(x) |
Абсолютное значение комплекс- |
|
ного числа |
||||
|
|
|
||
tanh(x) |
Гиперболический тангенс |
angle(x) |
Аргумент комплексного числа |
|
|
|
|
Образование комплексного числа |
|
atan(x) |
Арктангенс |
complex(x,y) по действительной и мнимой |
||
|
|
|
частям |
|
atan2(x) |
Четырехквадрантный |
conj(x) |
арктангенс |
||
atanh(x) |
Гиперболический арктангенс |
imag(x) |
sec(x) |
Секанс |
real(x) |
sech(x) |
Гиперболический секанс |
unwrap(x) |
asec(x) |
Арксеканс |
isreal(x) |
asech(x) |
Гиперболический арксеканс |
cpxpair(x) |
csc(x) |
Косеканс |
fix(x) |
csch(x) |
Гиперболический косеканс |
floor(x) |
acsc(x) |
Арккосеканс |
ceil(x) |
acsch(x) |
Гиперболический арккосе- |
round(x) |
канс |
||
cot(x) |
Котангенс |
mod(x,y) |
coth(x) |
Гиперболический котангенс |
rem(x,y) |
acot(x) |
Арккотангенс |
|
Комплексно-сопряженное число
Мнимая часть комплексного числа Действительная часть комплексного числа
Непрерывная функция фазового угла Истинно, если массив действительных чисел
Сортировка комплексносопряженных пар чисел Усечение дробной части числа Округление до меньшего целого Округление до большего целого Округление до ближайшего целого Остаток в смысле модульной арифметики
Остаток от деления
В MATLAB имеется несколько переменных с заранее закрепленными за ними именами. Это pi, Inf, NaN, i, j. На рис. 1.4 приведены три примера. NaN (сокращение от Not-a-Number) используется для обозначения неопределенного (нечислового) результата операции. Inf соответствует +∞ , а pi – числу π. Переменные i и j обозначают мнимую единицу и используются при арифметических операциях с комплексными числами.
С помощью функции who можно вывести на экран список всех переменных, хранящихся в рабочей области. Функция whos позволяет вывести на экран список переменных в рабочей области вместе с дополнительной информацией об их типе, размерности и занимаемой памяти.
6
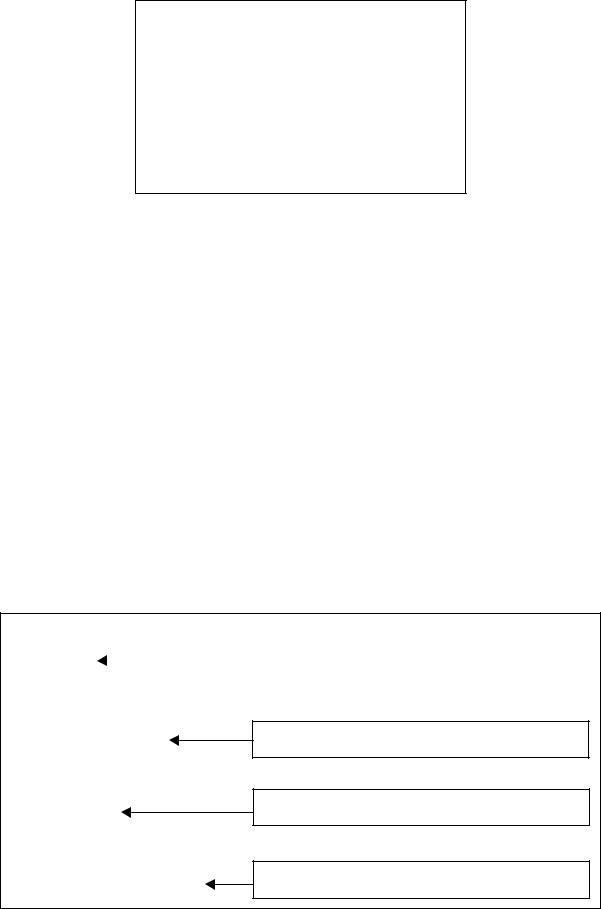
>>z=3+4*i
z =
3.0000 + 4.0000i
>>Inf
ans = Inf >> 0/0
Warning: Divide by zero. ans =
NaN
Рис. 1.4. Три переменные с заранее закрепленными за ними именами: i, Inf, и NaN
Переменные можно удалить из рабочей области с помощью функции clear. Собственно функция clear удаляет из рабочей области все данные (переменные и функции); clear variables удаляет все переменные; clear name1 name2 и т.д. удаляет переменные name1, name2 и т.д.
Все вычисления в MATLAB выполняются с двойной точностью. Однако вывод чисел на экран может осуществляться в разных форматах. По умолчанию нецелые числа выводятся с четырьмя разрядами после десятичной точки, но с помощью функции format можно изменить формат вывода, как показано на рис 1.5. Если задан какой-то определенный формат, то он сохраняет силу до тех пор, пока не будет изменен. Формат вывода не влияет на внутренние вычисления в MATLAB. С другой стороны, количество выводимых разрядов не обязательно соответствует количеству значащих цифр числа. Из других форматов вывода (не указанных на рис. 1.5) отметим format long g (наилучший формат – 15 разрядов с фиксированной или плавающей точкой), format short g (то же самое, что format long g, но с 5 разрядами), format hex (шестнадцатеричный фор-
мат), format (то же, что и format short).
>>pi |
|
|
ans= |
5- разрядное число с фиксированной точкой |
|
3.1416 |
|
|
|
|
|
>> format long; pi |
|
ans= |
15разрядное число с фиксированной точкой |
3.14159265358979 |
>> format short e; pi ans=
3.1416e+00
>> format long e; pi ans= 3.141592653589793e+00
5- разрядное число с плавающей точкой
15разрядное число с плавающей точкой
Рис. 1.5. Иллюстрация четырех форматов вывода чисел
7

Матрицы
MATLAB – это сокращенно матричная лаборатория. Рассмотрим интерактивные возможности MATLAB, облегчающие анализ и синтез систем управления. Начнем с ведения основных понятий, поясняющих действия с матрицами и векторами.
Основной вычислительной единицей является матрица. Векторы и скаляры можно рассматривать как частные случаи матрицы. Матрица обычно заключается в квадратные скобки, [ ]. Элементы столбца отделяются пробелами или запятыми, а строки точками с запятой или возвратом каретки. Предположим, что нам надо ввести матрицу А следующего вида:
|
1 |
A = |
log(−1) |
arcsin(0.8)
−4 j |
2 |
sin(π 2) |
cos(π 3) . |
arccos(0.8) |
exp(0.8) |
|
|
Одним из способов ввода (отнюдь не единственный) приведен на рис. 1.6. Матрицы можно вводить посредством записи нескольких строк, завершая их точкой запятой и возвратом каретки или просто возвратом каретки. Это
очень удобно при вводе больших матриц. Для разделения столбцов можно использовать различные комбинации пробелов и запятых, а для разделения строк
– различные комбинации точек с запятой и возврата каретки, как показано на рис. При вводе матриц нет необходимости в специальных инструкциях, указывающих их тип или размерность; память под матрицы отводится автоматически. Заметим также, что элементы матриц могут быть комплексными числами либо содержать тригонометрические и элементарные математические функции.
>>A=[1,-4*j,sqrt(2); |
|
|
|
|
|
Матрица комплексных |
|||||
|
|
|
|
|
чисел размерности 3×3 |
||||||
log(-1) sin(pi/2) cos(pi/3) |
|
|
|
||||||||
|
|
|
|
|
|
||||||
asin(0.5), acos(0.8) exp(0.8)] |
|
|
|
|
|
|
|||||
A = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Возврат каретки |
|
|
|
1.0000 |
0 - 4.0000i |
1.4142 |
|
|
|
|
|
||||
|
|
|
|
||||||||
0 + 3.1416i |
1.0000 |
|
|
0.5000 |
|
|
|
|
|
||
0.5236 |
0.6435 |
|
|
2.2255 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
>> A=[1 2;4 5] |
|
|
|
|
|
|
Матрица действительных чисел |
|
|||
|
|
|
|
|
|
|
размерности 2×2 |
|
|||
A = |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
45
Рис. 1.6. Матрица с вещественными и комплексными элементами вводится
савтоматическим определением ее размерности и типа элементов
Косновным матричным операциям относятся сложение, вычитание, транспонирование, возведение в степень и так называемые операции над мас-
8
сивами. Символы математических операций над матрицами приведены в табл. 1.1. MATLAB имеет возможность левостороннего и правостороннего деления матриц.
Матричные операции требуют согласование размерностей. Это означает, что при сложении и вычитании они должны иметь одинаковую размерность. Если матрица А имеет размерность n×m, а матрица В – размерность p×r, то A±B имеет смысл только тогда, когда n=p, а m=r. Умножение матриц А*В возможно только в случае m= p. Особым случаем является умножение матрицы на вектор. Предположим, что b есть вектор (столбец) из p элементов. В результате будет получен вектор размерности n×1. Примеры основных матричновекторных операций приведены на рис. 1.7.
>> A=[1 3;5 9]; B=[4 -7;10 0]; |
|
||
>> A+B |
Сложение матриц |
||
ans = |
|
||
|
|
||
5 |
-4 |
|
|
15 |
9 |
|
|
>> b=[1;5]; |
Умножение матриц |
||
>> A*b |
|||
|
|||
ans = |
|
|
|
16 |
|
|
|
50 |
|
|
|
>> A' |
|
Транспонирование матрицы |
|
ans = |
|
|
|
1 |
5 |
|
|
3 |
9 |
|
|
Рис. 1.7. Три основные матричные операции: сложение, умножение и транспонирование |
|||
>> x=[5;pi;sin(pi/2)];y=[exp(-0.5);-13;pi^2];
>> x'*y  Внутреннее произведение ans =
Внутреннее произведение ans =
-27.9384
>> x*y' |
|
|
|
Внешнее произведение |
|
|
|
|
|
ans = |
|
|
|
|
|
|
|
|
|
3.0327 |
-65.0000 |
49.3480 |
|
|
1.9055 |
-40.8407 |
31.0063 |
|
|
0.6065 |
-13.0000 |
9.8696 |
|
|
Рис. 1.8. Внутреннее и внешнее произведение двух векторов
9
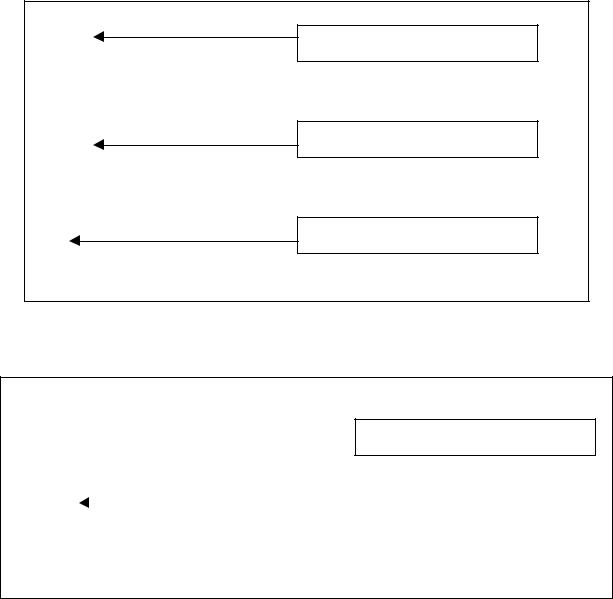
Транспонирование матрицы обозначается символом апострофа (′). С помощью операций транспонирования и умножения можно получить так называемое внутреннее произведение векторов. Поясним это на примере. Предположим, что w и v есть векторы размерности m×1. Тогда их внутреннее произведение находится как w′* v. Внутреннее произведение двух векторов дает скалярную величину. Аналогично можно вычислить внешнее произведение двух векторов как w* v′. Внешнее произведение двух векторов дает скалярную величину размерности m×1 дает матрицу размерности m×m, ранг которой равен 1. Примеры внутреннего и внешнего произведений приведены на рис. 1.8.
Основные матричные операции можно заменить поэлементными действиями с использованием периодически действующего оператора. Такие процедуры известны как операции над массивами. Самые простые операции над массивами приведены в табл. Операции сложения и вычитания являются простейшими и не требуют указания дополнительного периода, соответствующему оператору. Однако при умножении, делении и возведении матрицы в степень обязательно надо указывать точку перед символом операции, как показано в табл. 1.2.
Таблица 1.2. Математические операторы, применяемые к массивам
+ |
Сложение |
- |
Вычитание |
.* |
Умножение |
./ |
Деление |
.^ |
Возведение в степень |
Рассмотрим матрицы А и В размерности 2×2:
a11 |
a12 |
|
|
b11 |
b12 |
|
A = a |
a |
|
, |
B = b |
b |
. |
21 |
22 |
|
|
21 |
22 |
|
Применив оператор умножения массивов, мы получим:
a11b11 |
a12b12 |
|
A.*B = a b |
a b |
. |
21 21 |
22 22 |
|
Элементы произведения А.*В являются произведениями соответствующих элементов А и В. Примеры действий с двумя массивами приведены на рис. 1.9.
Остановимся на представлении данных с использованием двоеточия.
Такое представление, описание которого приведено на рис. 1.10, позволяет сформировать вектор, компонентами которого являются числа, начинающиеся со значения xi и заканчивающегося значением xf , следующие друг за другом с
заданным шагом dx.
10
