Формулы Ньютона-Котеса

Если подынтегральную функцию заменить каким-либо интерполяционным многочленом, то получим квадратурные формулы вида:

где х_к– выбранные узлы интерполяции;A_k– коэффициенты, которые зависят от выбранных узлов, но не зависят от вида функцииf(x);R – остаточный член, определяющий максимальную ошибку при использовании квадратурной формулы;k=0, 1, …,n.

Разбивая отрезок интегрирования [a, b] наnравных частей системой точек

x_k = x₀+kh; k=0, 1, …, n; x₀=a; x_n=b

и вычисляя подынтегральную функцию в полученных узлах

y_k=f(x_k); k=0, 1, …, n,

получают квадратурные формулы для равноотстоящих узлов. Эти формулы называютформулами Ньютона-Котеса. Наиболее удобны при численном интегрировании интерполяционные многочлены невысоких порядков, при использовании которых получают достаточно простые составные формулы.

Формула трапеций.

Формула трапецийполучается в случае использования интерполяционного многочлена 1-го порядка:

Остаточный член имеет вид: Использование формулы трапеций при вычислении определенного интеграла приводит к ошибкегде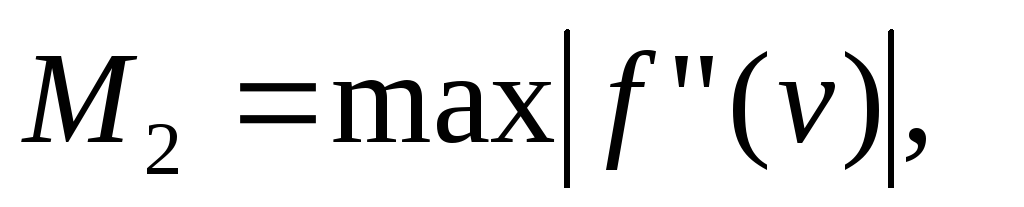

Для нахождения приближенного значения определенного интеграла по формуле трапеций можно использовать алгоритм, схема которого представлена на рис. 5.5.

Ошибка ограничения для метода трапеций больше, нежели чем для других формул Ньютона-Котеса, но его привлекательность заключается в простой реализации. Кроме того, незначительное усложнение алгоритма позволяет существенно снизить погрешность вычислений, поэтому формула трапеций достаточно часто используется (в сочетании с другими формулами).

Рис. 5.5 Алгоритм вычисления определенного

интеграла по формуле трапеций

Формула парабол (Симпсона)

Используя интерполяционный многочлен 2-го порядка (параболу) получают формулу численного интегрирования – формулу Симпсона:

где

На рис. 5.6 показана схема алгоритма, реализующего вычисления по формуле парабол. При реализации формулы число узлов обязательно нечетно, т. е. число участков разбиения интервала интегрирования должно быть четным: n=2m. В алгоритме использован прием, при котором число повторений цикла уменьшается в два раза, т. е. дважды реализуется модификация параметра цикла, что уменьшает время выполнения алгоритма. Метод Симпсона считается одним из наиболее применяемых методов численного интегрирования, обеспечивающим достаточно хорошую точность вычислений.

Рис. 5.6 Алгоритм вычисления определенного

интеграла по формуле Симпсона

Алгоритм вычисления суммы бесконечного ряда

Характерным примером итерационных циклов является задача вычисления суммы бесконечного ряда:

где t_n(x)– слагаемое, зависящее от параметраx (в общем случае) и номераn. Вычисляемая последовательность

где – частная сумма.

Для контроля погрешности можно использовать последовательность

где t_n(x) =s_n(x) –s_n-1(x) – слагаемые рядаn.

.

Условие выхода из итерационного цикла (справедливо при знакопеременном ряде {t_n(x)}):

| t_n (x ) | <.

Алгоритм вычисления бесконечной суммы является модификацией одного из алгоритмов вычисления конечной суммы. Если применение рекуррентных формул нецелесообразно, то вычисления будут наиболее эффективными, если каждое слагаемое определять по общей формуле и полученные значения накапливать в некоторой переменной. Общий вид схемы алгоритма, реализующего вычисление бесконечной суммы с погрешностью с помощью цикла с предусловием, показан на рис. 5.10, а.

Если для вычисления слагаемых используются рекуррентные соотношения

то общая схема итерационного алгоритма для вычисления бесконечной суммы показана на рис. 5.10, б.

Например, тригонометрическая функция sin(x) может быть представлена в виде бесконечной суммы

В данном случае

тогда

Теперь можно определить

Начальное значение слагаемого находим по формуле