
Мат. анализ, 2 часть; 1 семестр(2)
.pdf
Выберем в качестве наименьшее из чисел 1, 2, 3 . Тогда внутри U (t0 ) будут справедливы все три неравенства:
|
|
xR x(t) |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
yR |
y(t) |
|
. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
zR |
z(t) |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из последнего следует, что |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x t xR 2 y t yR 2 z t zR 2 3 2 . |
|||||||||
|
r t R |
|
|
|||||||||||||||||
Итак, для произвольно выбранного числа 0 |
мы нашли такое, что |
|||||||||||||||||||
при x U (t0) |
справедливо неравенство |
|
r t R |
|
, что и означает, что |
|||||||||||||||
|
|
|||||||||||||||||||
limr(t) R .
t t0
Теорема доказана.
Опр. Векторная функции r(t) называется непрерывной в точке t0 , если существует предел r(t) при t t0 и он равен
limr t r(t0).
t t0
Очевидно, определение непрерывности вектор-функции также формально не отличается от определения непрерывности обычной функции. Переформулируем
это определение в терминах приращений.
Пустьt t0 , r t0 x t0 i y t0 j z t0 k .
Придадим аргументу t приращение t .
r t t x t0 t i y t0 t j z t0 t k.
Вектор r r t0 t r t0 называется приращением вектор-функции r(t) в
точке t0 , отвечающим приращению t независимой переменной t (рис. 4).
Очевидно, что
r (x t t0 x(t0))i (y t t0 y(t0)) j (z t t0 z(t0))k,
т.е. |
|
r xi yj zk. |
(2) |
Рис. 4. Приращение вектор-функции.
71

Опр. Векторная функция r(t)называется непрерывной в точке t t0 , если бесконечно малому приращению аргумента t в этой точке отвечает бесконечно малое приращение функции r(t):
lim r 0.
t 0
§3. Производная векторной функции.
Опр. Производной векторной функции r(t) называется предел отношения приращения вектор-функции к приращению аргумента при стремлении последнего к нулю:
r'(t) dr lim r . dt t 0 t
Из формулы (2) и определения производной вектор-функции очевидно, что
dr xi' y' j z'k. dt
Выясним геометрический смысл производной векторной функции. Пусть
начало вектора |
r(t) находится в начале координат. При t t0 конец вектора r |
||||||||
находится в точке M , а при t t0 t – в точке N . Приращение r , |
отвечающее |
||||||||
изменению t , |
r MN (рис. 4). |
|
|
||||||
Поэтому |
|
|
|
|
|
|
|
||
|
|
|
|
r |
|
|
t возрастает |
|
|
|
r |
|
|
MN при t 0 |
|
||||
|
|
|
|
||||||
|
|| MN, |
причем t |
|
|
|
||||
|
|
|
|
|
|||||
|
t |
|
|
r |
|
t убывает . |
|
||
|
|
|
|
|
|
|
MN при t 0 |
|
|
|
|
|
|
t |
|
||||
|
|
|
|
|
|
|
|
||
Иными словами, вектор |
|
r |
параллелен вектору MN и направлен |
в сторону |
|||||
|
t |
||||||||
|
|
|
|
|
|
|
|
||
возрастания переменной t.
Рассмотрим годограф вектор-функции r(t). Очевидно, что отрезок MN есть хорда годографа, а прямая, являющаяся продолжением этого отрезка – секущей годографа. При стремлении t 0 точка N перемещается по годографу, стремясь к точке M . Поскольку предельное положение секущей кривой – есть касательная к этой кривой, то вектор
r' dr dt
направлен вдоль касательной к годографу векторной функции r(t) в точкеt0 в
сторону возрастания переменной t. Наконец, найдем модуль вектора r' :
|r' t0 |
| |
lim |
r |
|
lim |
|
s |
|
lim |
|
l |
|
|
dl |
, |
|
t |
t |
|
||||||||||||
|
|
t 0 t |
|
t 0 |
|
t 0 |
|
|
dt |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где dl – дифференциал длины дуги кривой L. Здесь мы воспользовались тем, что
| r | s |MN |, l ~ s при s 0, а при t 0, очевидно, s 0.
72
Итак, производная векторной функции r(t)– есть вектор, направленный по касательной к годографу этой функции в направлении роста независимой переменной t. Длина этого вектора равна производной длины дуги в точке t0 .
Выясним теперь механический смысл производной векторной функции. Рассмотрим частицу (материальную точку), движущуюся в пространстве
произвольным образом по некоторой траектории (рис. 5). Пусть r(t)– радиусвектор частицы в текущий момент времени t. Тогда, как уже говорилось выше, годограф – это траектория (путь) движения частицы.
Рис. 5. Движение частицы в пространстве.
Опр. Средней скоростью частицы за промежуток времени (t0 ,t0 t)
называется вектор
vср r .
t
Опр. Мгновенной скоростью движения частицы в момент времени t0
называется предел средней скорости за промежуток t при t 0, т.е. вектор
|
limv |
lim |
r |
r'. |
|
v |
|||||
|
|||||
|
t 0 ср |
t 0 t |
|||
§4. Уравнение касательной к пространственной кривой.
Пусть пространственная кривая L задана уравнением:
r x t i y t j z t k.
Пусть M(x0, y0,z0) – произвольная точка, лежащая на этой кривой, и
соответствующая значению t t0 : x0 x(t0), y0 y(t0), z0 z(t0). Поскольку вектор r'(t0 ) x' t0 , y' t0 ,z' t0 направлен по касательной к годографу вектор-функции
r(t), он является направляющим вектором касательной к кривой L. Поэтому уравнение касательной к кривой L в точке M имеет вид:
x x0 |
|
y y0 |
|
z z0 |
|
|
|
|
|
|
. |
x' t0 |
y' t0 |
z' t0 |
|||
73

§5. Правила дифференцирования векторной функции.
Справедливы следующие формулы дифференцирования векторной функции.
1)r1(t) r2(t) ' r1' r2', при условии, что две последние производные существуют.
2)(cr t )' cr ', где c – постоянная.
3) |
f |
t r(t) ' |
f ' t r t f (t)r'(t), где |
f (t) – |
обычная |
функция (R R ). |
|||||
|
|
|
|
|
|
|
|
|
и r'(t). |
|
|
|
Подразумевается существование производных f '(t) |
|
|
||||||||
4) |
(r |
r )' |
r' r r r ', где точка обозначает скалярное произведение двух вектор- |
||||||||
|
1 |
2 |
1 |
2 |
1 |
2 |
|
|
|
|
|
|
функций. Подразумевается существование производных r' и r ' . |
|
|||||||||
|
|
|
' |
|
|
|
|
|
1 |
2 |
|
5) |
|
|
|
где крестик |
обозначает |
векторное |
произведение двух |
||||
(r |
r )' |
r |
r |
r |
r ' , |
||||||
|
1 |
2 |
1 |
2 |
1 |
2 |
|
|
|
|
и r ' . |
|
вектор-функций. Подразумевается существование производных r' |
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
§6. Теорема о производной вектор-функции постоянной длины.
Пусть r t - вектор функция, причем Причем r t const т.е. от t зависит только название вектора r . В этом случае будем называть вектор-функцию r t
вектор-функцией постоянной длины.
Теорема. Производная вектор-функции постоянной длины длины r(t)– есть
вектор, перпендикулярный к самому вектору r(t): r r ' 0.
Доказательство. Производная скалярного квадрата вектора r , очевидно,
равна:
(r r)' r' r r r' 2r r'.
Сдругой стороны, та же производная равна:
r r ' r 2 ' 0,
поскольку
r t const.
Таким образом, r r ' 0.
Теорема доказана.
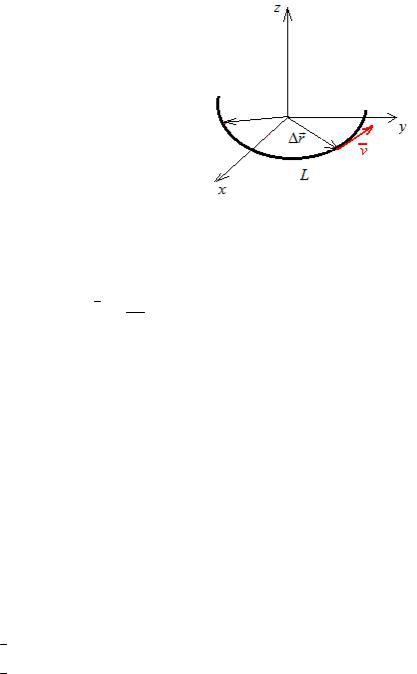
Физический смысл этой теоремы состоит в том, что тангенциальная скорость частицы, движущейся по поверхности сферы (в частности – по окружности), перпендикулярна радиус-вектору частицы.
Геометрический смысл этой теоремы состоит в том, что касательная прямая к сфере (окружности) в точке касания перпендикулярна радиус-вектору этой точки.
74
