Мат. анализ, 2 часть; 1 семестр(2)

7.'(x) 0, в u(a);

8.lim f '(x) A.

x a '(x)

Тогда существует

Замечание. Правило Бернулли-Лопиталя дает достаточное, но необходимое условие

существовать.

Пример. Предел отношения функций

lim x sin x

x x

с неопределенностью существует и равен единице. Действительно,

§6. Раскрытие неопределённостей других видов.

Мы видели, что правило Бернулли-Лопиталя можно использовать для раскрытия

0 = 1 = .

Под этими «символическими» преобразованиями подразумеваются со ответствующие преобразования над функциями, стоящими под знаком предела. Например, первая последовательность преобразований означает следующее:

31

Очевидно, последний предел содержит неопределенность 0 . После преобразования

0

произведения в дробь (преобразования типа неопределенности), используется правило Бернулли-Лопиталя. На практике все выглядит гораздо проще и естественней, чем в теории.

Пример.

x 0 2cosx xsinx

3. На равнее с неопределенностью 1 существуют также неупоминавшиеся ранее неопределенности 00 и 0 . Все три типа неопределенностей преобразуются в неопределенность 0 по одной и той же схеме:

1 eln1 e ln1 e 0

Здесь мы воспользовались результатами первого примера.

§7. Сравнение роста показательной, степенной, и логарифмической функций при x .

Покажем, что при больших x любая показательная функция (с основанием больше единицы) растет быстрее степенной (с положительным показателем), а степенная

– быстрее логарифмической. Нам понадобится следующее определение.

Опр. Факториалом натурального числа n («n-факториал») называется произведение натуральных чисел от 1 до n:

n! 1 2 3 ... n.

Факториал нуля по определению равен единице: 0! 1.

Пример. 5! 1 2 3 4 5 120.

1) Рассмотрим степенную функцию с натуральным показателем f (x) xn , n N и показательную функцию с основанием больше единицы:

32

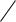
g(x) ax a 1.

Покажем, что показательная функция имеет высший порядок роста, по сравнению со степенной при

x .

Можно показать, что это равенство справедливо не только для натуральной степени:

0 x o(ax ) при x .

Итак, показательная функция при x→+∞ растёт быстрее любой степени x. В частности, x o ( e x ) при x .

2) Рассмотрим теперь степенную функцию с положительным показателем и натуральный логарифм: f (x) x , 0, g(x) ln x. Покажем, что степенная функция имеет высший порядок роста по сравнению с логарифмом при x . Действительно,

Таким образом,

ln x o(x ) при x .

Это равенство справедливо и для логарифма с произвольным основанием a 1: loga x o(x ) при x .

3) С учетом сказанного, очевидно, что показательная функция имеет высший порядок роста по сравнению с логарифмической при x :

loga x o(bx ) при x

(a,b 1).

Лекция № 11

§1. Формула Тейлора.

Пусть функция y f (x), определенная в некоторой окрестности точки x0 ,

дифференцируема в этой точке. Тогда, как известно, приращение данной функции в точке x0 представимо в виде:

y f (x) f (x0) f '(x0) x o( x) , где x x x0 .

Иными словами,

f(x) f(x0) f '(x0)(x x0) o(x x0) при x x0.

Это равенство представляет собой формулу Тейлора 1-го порядка. Как мы видели ранее, оно позволяет сколь угодно точно вычислить значения функции при достаточно малых x . Однако, при больших x точность приближения функции по этой формуле будет плохой. В общем случае, формула Тейлора позволяет приближать функцию f(х) многочленом n-ой степени, причем, выбирая достаточно большое n, можно получить сколь угодно высокую точность приближения.

33

Пусть функция y f (x) определена в некоторой окрестности точки x0 и имеет в этой окрестности все производные, вплоть до (n 1) -го порядка включительно. Построим

многочлен Pn(x), удовлетворяющий следующим условиям:

Эти условия позволяют предположить, что многочлен будет достаточно хорошо приближать функцию f (x) при x близких к x0 , действительно, в точке x0 значение

многочлена совпадает со значением функции, «скорость» изменения значения многочлена

– со «скоростью» изменения значения функции, «ускорение» изменения значения многочлена – с «ускорением» изменения значения функции и т.д.

Будем искать этот многочлен в виде:

...

Pn(n) (x) n(n 1)(n 2) ... 3 2 1 Cn Cnn!

С учетом условий (1), найдем:

Таким образом,

34

Это равенство называется формулой Тейлора n-го порядка, а функция Rn (x) –

остаточным членом формулы Тейлора.

§2. Формула Тейлора с остаточным членом в форме Пеано.

Покажем, что остаточный член формулы Тейлора пренебрежимо мал при х достаточно близких к x0 , точнее, что Rn (x) o((x x0)n ) при x x0 . Тем самым мы убедимся, что многочлен Тейлора действительно хорошо приближает функцию f (x) в

малой окрестности точки x0 .

Rn (x0) 0

Rn '(x0) 0

Из (1) и (3) следует, что Rn ''(x0) 0.

...

Rn(n)(x0) 0

С учетом этого,

Таким образом,

Rn (x) o((x x0)n ) при x x0 .

Остаточный член, записанный в такой форме называется остаточным членом в форме Пеано. Формула Тейлора с остаточным членом в форме Пеано имеет вид:

стремится к нулю при x x0 .

§3. Формула Тейлора с остаточным членом в форме Лагранжа.

Получив остаточный член в форме Пеано, мы показали, что многочлен Тейлора хорошо приближает функцию в малой окрестности точки x0 , но ничего не выяснили о

35

точности этого приближения. Остаточный член можно записать также в другой форме, называемой формой Лагранжа. Остаточный член в форме Лагранжа позволяет оценить погрешность приближения функции по формуле Тейлора.

Теорема (о представимости функции по формуле Тейлора с остаточным членом в

§4. Формула Маклорена.

Выбирая x0 0, получим частный случай формулы Тейлора, называемый формулой Маклорена:

Формула Маклорена с остаточным членом в форме Пеано имеет вид:

Формула Маклорена с остаточным членом в форме Лагранжа имеет вид:

где c 0;x при x 0и c x;0 при x 0 .

§5. Представление по формуле Маклорена элементарных функций.

1. Представим экспоненту y ex по формуле Маклорена.

Таким образом, представление функции y ex по формуле Маклорена с остаточным членом в форме Лагранжа имеет вид:

где c 0;x при x 0и c x;0 при x 0 .

а представление по формуле Маклорена с остаточным членом в форме Пеано:

36

2.Представим по формуле Маклорена функцию y sin x .

...

а представление по формуле Маклорена с остаточным членом в форме Пеано:

3. Аналогичным образом, можно получить представление по формуле Маклорена с остаточным членом в форме Лагранжа и в форме Пеано функции y cosx:

37

Получаем следующее представление по формуле Маклорена с остаточным членом в форме Лагранжа:

и с остаточным членом в форме Пеано:

y x x2 x3 x4 ... 1 n 1 xn o(xn ).

Лекция 12

§6. Применение формулы Тейлора (Маклорена) для вычисления приближенных значений функции.

Рассмотрим конкретный пример применения формулы Тейлора для приближенного вычисления значений функции. Найдем приближенное значение числа e. Число e есть значение функции y ex в точке x 1. Используя представление экспоненты по формуле Маклорена третьего порядка, получим:

e 1 1 1 1 2.63. 2 6

Остаточный член в форме Лагранжа позволяет оценить погрешность этого приближения:

R ec 1 1 0.125, поскольку 0 c 1, а e 3. 4! 8

38

Увеличивая порядок формулы Маклорена, мы увеличим точность приближения. Так, используя формулу Маклорена пятого порядка, найдем:

§7. Асимптоты графиков функций.

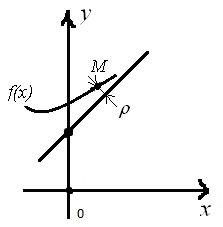
Опр. Асимптотой графика функции называется прямая, расстояние от которой до точки графика стремится к нулю при бесконечном удалении этой точки от начала координат (рис. 1).

Рис. 1. Асимптота графика функции.

Замечание. Очевидно, что при бесконечном удалении точки графика от начала координат хотя бы одна из координат этой точки стремится к бесконечности. Поэтому определение асимптоты можно сформулировать и так:

Опр. Асимптотой графика функции называется прямая, расстояние от которой до точки графика стремится к нулю, когда одна из координат этой точки (возможно обе координаты) стремится к бесконечности.

Существует два вида асимптот: вертикальные и наклонные. Частным случаем наклонной асимптоты является горизонтальная асимптота. Изучим последовательно различные виды асимптот.

графика функции y f (x). Пример вертикальной асимптоты представлен на рис. 2. В

Очевидно, что вертикальная асимптота удовлетворяет общему определению асимптоты: расстояние от точки графика функции y f (x) до прямой x x0 стремится к нулю при стремлении ординаты точки графика к бесконечности ( y ).

39