Elektrotekhnika_Lektsii

Здесь

g 1r - активная проводимость,

bL 1 - индуктивная проводимость.

L

Единица измерения проводимостей - сименс (Сим). Векторная диаграмма токов приведена на рис. 2.12.

ICm

Irm Um

ILm

Im

Рис.2.12

41

jIm

jbC

g

Rl

jbL

Y

Рис.2.13

Комплексная векторная диаграмма токов для уравнения (12) приведена на рис. 2.14.

jIm

Пример 1.

Для схемы, приведенной на рис. 2.15.

42

i1 r1

u(t)

Рис.2.15

Задано:

u(t) 202 sin( t 45o ) ,

Воспользуемся комплексным методом расчета. Запишем комплексы сопротивлений для каждой ветви:

Z1 r1 2,8Ом

43

Мгновенные значения токов запишем в виде:

i1 25sin t

i2 25sin t 57

i3 15,852 sin t 64 22,35sin t 64

Пример 2.

Рис.2.11

Для схемы рис. 2.11 определить сдвиг по фазе между входным током и

напряжения принята за ноль, а фаза тока получилась равной 4 . Сдвиг по

фазе между током и напряжением 4 .

44

P 1 T p(t)dt I 2 r UI cos

T 0

45

амперах, (ВА).

Мощности P и S связаны по закону треугольника мощностей, рис 2.17.

S' Q

P

Рис.2.17

Третья составляющая в этом треугольнике – мощность реактивная

Рис.2.19

Максимальное и минимальное значения мощности соответственно равны 800 и 200 ВА. Определить полную активную и реактивную мощности цепи. Решение:

Размах значений мощности 1000 ВА, амплитудное значение 500 ВА, это полная мощность S. Среднее значение мощности P=800-500=300 Вт.

Реактивная мощность Q 5002 3002 400BAP .

Отношение активной мощности к полной (рис. 2.17) равное косинусу угла сдвига фаз между напряжением и током, называется коэффициентом мощности

46

Для лучшего соотношения между мощностью электрической машины и других приборов и их габаритными размерами коэффициент мощности стремятся сделать максимально возможным.

Высокий коэффициент мощности желателен для уменьшения потерь при передаче энергии по линиям.

Чтобы выразить мощность через комплексы токов и напряжений воспользуемся следующим соображением.

Активная мощность должна быть равна P UI cos , где н j .

Отсюда следует, что при определении комплекса мощности фаза тока должна быть взята с обратным знаком, т.е. комплекс тока должен быть заменен на сопряженный.

Полная комплексная мощность

UIe j UI cos jUI sin P jQ

2.10.Законы Кирхгофа и уравнение энергетического баланса в комплексной форме.

Первый закон Кирхгофа:

Уравнение энергетического баланса:

Sист Sпотр .

Pист Pпотр .

Qист Qпотр .

2.11. Резонанс в цепях синусоидального тока.

Реактивные сопротивления и проводимость являются частотно-зависимыми величинами. Следовательно, при последовательном или параллельном соединении элементов L и C возможна на какой-то частоте полная компенсация реактивных сопротивлений или проводимостей. Режим, при

47

котором наступает компенсация, называют резонансом. При резонансе входное сопротивление цепи становится активным, входное напряжение совпадает по фазе с входным током, а полная мощность будет активной.

Угловая частота, 0 , при которой наступает резонанс, называется

резонансной или собственной угловой частотой цепи. Различают две разновидности резонанса: резонанс напряжений и резонанс токов.

2.11.1. Резонанс напряжений.

Может возникнуть в цепи с последовательным соединением L и C, рис. 2.20а.

48

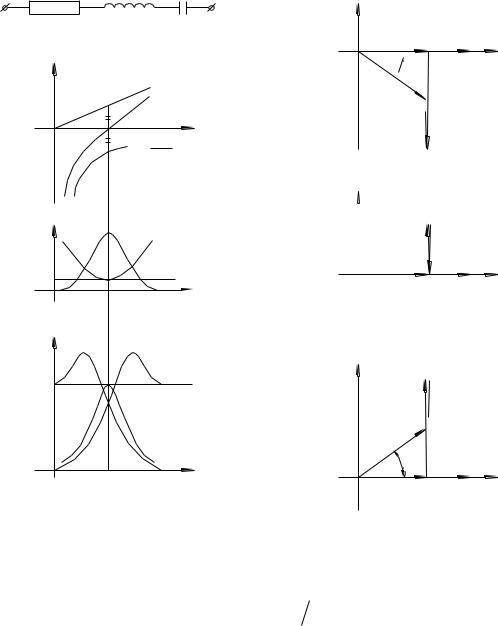
Настройку цепи в резонанс, изменение параметров цепи при частотах , отличных от резонансной можно увидеть, если построить частотные характеристики сопротивлений, тока в цепи и напряжений на r, L, C.

На рис. 2.20б,в,г приведены частотные характеристики реактивных

также амплитудно-частотные характеристики напряжений:

По графику jx определена резонансная частота 0 , по графику можно увидеть, что сопротивление цепи при резонансе минимально и равно активному сопротивлению, по графику I - что ток в цепи при резонансе

максимален. Графики Ur , uL , uC имеют ярко выраженный избирательный характер, т.е. имеют максимальные значения на резонансной

частоте или вблизи нее. Можно также отметить, что напряжения U L и UС

при резонансе могут превышать значение входного напряжения. Это хорошо иллюстрируется с помощью векторных диаграмм напряжения приведенных

значения с характером реактивных сопротивлений на соответствующих частотах. Так при частотах 0 , реактивное сопротивление носит емкостной характер и cos 0 и т.д.

49

2.11.2. Резонанс токов.

Возможен в цепях с параллельным соединением L и C элементов, рис. 2.21а.

Для этой цепи запишем уравнение по первому закону Кирхгофа:

Компенсация реактивных проводимостей и реактивных токов:

50