Задание 2. Пользуясь алгоритмом Евклида вычислить нод и выразить его через исходные числа: (2576; 154).

НОД (2576;154) по алгоритму Евклида (метод деления):

				2576	154
				2464	16
			154	112
			112	1
		112	42
		84	2
	42	28
	28	1
28	14
28	2
0

1. , (Так записывать нельзя, т.к. равенства нет. Либо в строчку, как в теореме деления с остатком, либо использовать функцию [x] – целая часть х.) остаток 112. Продолжаем деление пока остаток не будет равен нулю.

2. остаток 42.

3. , остаток 28.

4. = 1, остаток 14.

5. = 2, остаток 0. Остаток равен нулю, значит НОД равен предыдущему остатку от деления.

Ответ: НОД (2576; 154) = 14.

Исправление:

Шаг 1:

2576	154
2464	16
112

остаток 112. Продолжаем деление пока остаток не будет равен нулю.

Шаг 2:

154	112
112	1
42		остаток 42.

Шаг 3:

112	42
84	2
28		остаток 28.

Шаг 4:

42	28
28	1
14		остаток 14.

Шаг 5:

28	14
28	2
0		остаток 0.

Остаток равен нулю, значит НОД равен предыдущему остатку от деления.

Ответ: НОД (2576; 154) = 14.

Расширенный алгоритм Евклида:

.

Подставим полученные значения в уравнение:

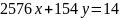
Переносим 14 в левую часть уравнения:

Поделим обе части исходного уравнения на НОД (2576;154) = 14:

НОД (184;11) = 1.

Коэффициенты уравнения:

Найдём частное решение исходного уравнения, используя цепные дроби

Для этого составим дробь, числителем которой будет наибольший по модулю коэффициент перед x или y, а знаменателем наименьший:

Таким образом, частное решение исходного уравнения имеет один из следующих четырех видов: .

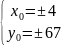Подставляя четыре значения в исходное уравнение, мы понимаем, что решение: . Уравнение приобретает вид:

(А как линейное представление НОД ищется из алгоритма Евклида?)

Ответ 1:

Если 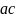  делится на b, с и b взаимно просты, то а делится на b.

Доказательство: так как  , то по теореме о линейном представлении НОД существуют числа u и v, для которых Тогда

Из условия следует, что слагаемое   делится на b, слагаемое  также делится на b. Отсюда, а делится на b.

(Вы не о том. Есть алгоритм нахождения линейного представления НОД через исходные числа на основе алгоритма Евклида.)

Ответ 2: Линейное представление НОД.

Теорема. Существуют целые числа u и v, удовлетворяющие уравнению линейного представления НОД:

Доказательство. Выражения для чисел u и v можно найти с помощью частных q_j из алгоритма Евклида. Из первого равенства алгоритма Евклида следует, что  т.е.

Подставляя это выражение во второе равенство алгоритма, получим

при

Подставляя найденные выражения в третье равенство, получим

при

Выдвинув индукционное предположение о справедливости представления «промежуточного» остатка

при

для всех 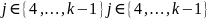из предпоследнего равенства алгоритма Евклида получим

т.е. закон формирования коэффициентов при A и B остается прежним. Но поскольку rk совпадает с НОД(A,B), то последнее равенство и дает требуемое линейное представление НОД: 

(Так и примените это в Вашем случае.)

Решение: Выразим НОД через исходные числа.

Пусть r₁=2576, r₂=154

s₁=1

s₂=0 заданы по условию

t₁=0

t₂=1

Используя формулы вычислим исходные числа.

q	r1	r2	R	S1	S2	S		t1	t2	t
16	2576	154	112	1	0	1		0	1	-16
1	154	112	42	0	1	-1		1	-16	17
2	112	42	28	1	-1	3		-16	17	-50
1	42	28	14	-1	3	-4		17	-50	67
2	28	14	0	3	-4	11		-50	67	-184
	14	0		-4	11		67		-184

Тогда

Значит, исходные числа: (-4) и 67.

Задание 3. Для (2576; 154) найти наименьшее общее кратное. Результат вычисления НОК проверить разложением чисел на простые множители.

Подставим значения в формулу вычисления наименьшего общего кратного через наибольший общий делитель

НОК (2576; 154) =

Ответ: НОК (2576; 154) = 28336

Проверка вычислений при помощи разложения чисел на простые множители:

2576 = 2 · 2 · 2 · 2 · 7 · 23

154 = 2 · 7 · 11

Чтобы определить НОК, необходимо недостающие множители добавить к множителям большего числа и перемножить их:

НОК (2576; 154) = 2 · 2 · 2 · 2 · 7 · 23 · 11 = 28336

Задание 4. Сократите следующие дроби, представив числитель и знаменатель дроби в каноническом виде:

Чтобы привести числитель и знаменатель в каноническую форму нам нужно упростить дробь: .

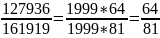(Чем подтвердите, что число 1999 просто?)

Канонический вид:

Исправление:

Чтобы упростить дроби, следует найти НОД (

				161919	127936
				127936	1
			127936	33983
			101949	3
		33983	25987
		25987	1
	25987	7996
	23988	3
7996	1999
7996	4
0

НОД ( .