
ЭАиТЧ Бунина А.В. ПР 8 ИБ-01б
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное образовательное
учреждение высшего образования
«Юго-Западный государственный университет»
Практическая работа №8
По дисциплине «Элементы алгебры и теории чисел»
Вариант №6
Выполнил: Бунина А.В.
студент группы ИБ-01б
Проверил: Добрица В.П.
профессор
Курск, 2021
Задание
1. Решить систему сравнений
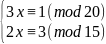 .
.
Так как (3, 20) = 1 и (2,15) = 1, то каждое из сравнений системы имеет решения (однако этого недостаточно для разрешимости системы).
Прибавляя
20 к правой части первого сравнения,
получим:
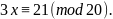
Отсюда,
разделив обе части сравнения на 3, будем
иметь:
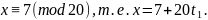
Подставляя это выражение во второе сравнение системы, будем иметь:
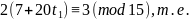
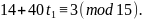
Так
как
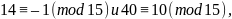 то отсюда получим:
то отсюда получим:
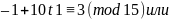
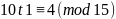
Так как (10, 15) = 5, и 4 не делится на 5, то полученное сравнение не имеет решений, а значит, и сама система не имеет решений.
Задание
2. Решить систему сравнений
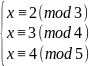 .
.
Из
первого сравнения системы получим:
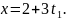
Подставляя
это выражение во второе сравнение
системы, будем иметь:
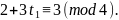
Отсюда
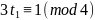 .
Прибавляя
к правой части число 8 = 4∙2, получим:
.
Прибавляя
к правой части число 8 = 4∙2, получим:
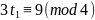 .
Разделив
обе части сравнения на 3, получим:
.
Разделив
обе части сравнения на 3, получим:
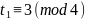
Следовательно,
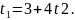
Отсюда
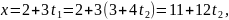 Подставляя это выражение в третье
сравнение системы, имеем:
Подставляя это выражение в третье
сравнение системы, имеем:
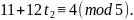
Так
как
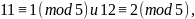 то отсюда получим:
то отсюда получим:
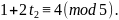
Тогда
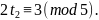 Прибавляя
к правой части сравнения число 5 будем
иметь:
Прибавляя
к правой части сравнения число 5 будем
иметь:
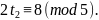
Отсюда,
разделив обе части сравнения на 2,
получим: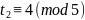
Следовательно,
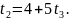 Отсюда
Отсюда
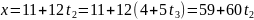 ,
т.е.
,
т.е.
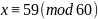 .
Это
и есть решение данной системы сравнений.
.
Это
и есть решение данной системы сравнений.
Проверка:
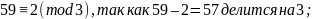
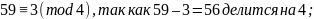
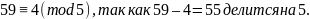
Получили верные сравнения, а значит система решена, верно.
