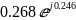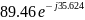Расчётно-графические работы / РГР 2 вар 5.2
.docxМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Тольяттинский государственный университет»
Институт химии и энергетики
Кафедра «Электроснабжение и электротехника»
13.03.02 «Электроэнергетика и электротехника»
Расчетно-графическая работа №2
Задача №2
по учебному курсу «Теоретические основы электротехники – 2»
Вариант 5.2
Группа: ЭЭТб-1901а
Студент: Назаров М.О.
Преподаватель: Шлыков С.В.
Тольятти 2021
«Расчет переходных процессов в линейных электрических цепях с сосредоточенными параметрами»
Цели и задачи:
Рассчитайте переходный процесс классическим методом, для этого величину одного из реактивных элементов (L или С) примите равным нулю. Определите законы изменения переходных напряжений на каждом элементе расчетной цепи. Следует учесть, что ключ S переключается из положения 1 в положение 2 в момент времени t = 0.
Рассчитайте переходный процесс в линейной электрической цепи с двумя реактивными элементами операторным методом. Определите
законы изменения переходных напряжений на каждом элементе расчетной цепи. Следует учесть, что ключ S переключается из положения 2 в положение 3 в момент времени t = 10τ.
Рассчитайте переходный процесс в линейной электрической цепи с двумя реактивными элементами методом переменных состояния и сравните с результатами расчета пункта 2. Следует учесть, что ключ S переключается из положения 2 в положение 3 в момент времени t = 10τ.
Запишите выражения переходных напряжений при переключении ключа S из положения 1, в положение 2 и в положении 3. Постройте графики переходных напряжений по представленным выражениям.
Задача № 2
Запишем исходные данные расчетной электрической цепи постоянного тока.
Источник входного воздействия задается схемой (рис. 1):
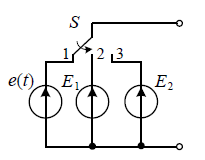
Рисунок 1 - Источник воздействия на расчётную электрическую цепь.
Дальше обратим внимание на саму цепь с нагрузкой, которая задаётся схемой (рис. 2)
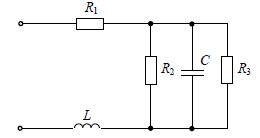
Рисунок 2 – Конфигурация расчётной электрической цепи с нагрузкой
Запишем исходные данные. По формулам, указанным ниже выполняется расчет всех неизвестных параметров.
Таблица 1 - Исходные данные.
Параметр |
Значение |
R1, Ом/км |
30 |
R1, Ом/км |
10 |
R1, Ом/км |
20 |
L, Гн |
0.6 |
C, мкФ |
25 |
E1, В |
150 |
E2, В |
280 |
Em, В |
90 |
ω, рад/с |
120 |
|
-0.3 |
Объединим схемы на рисунках 1 и 2 в одну (рис. 3):
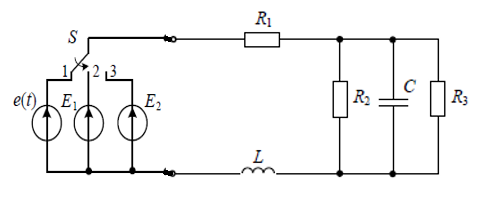
Рисунок 3 - Исходная расчетная электрическая цепь.
Проанализируем исходную электрическую цепь (рис. 3). До коммутации к нагрузке было подключено постоянное напряжение Е. В момент коммутации ключ из положения 1 переключается в положение 2 на источник переменного напряжение e(t). Через нагрузку начинает протекать переменное напряжение.
Найдем докоммутационные значения токов и напряжений. До коммутации источник переменного напряжения отключен от цепи, поэтому можно его временно удалить из схемы.
Анализ схемы дал понять, что электрическая цепь содержит 3 контура. В этих контурах присутствуют источник постоянного напряжения E, активные сопротивления R1,R2,R3, емкость С и катушка индуктивности L. На постоянном токе емкостное сопротивление равно бесконечности. Получается, что ток в цепи до коммутации будет равен нулю.
Если ток в цепи нулевой, тогда, согласно закону Ома, напряжение на сопротивлении R1 (формула 1):

Тогда получается, согласно II закону Кирхгофа, что все входное напряжение приложено к конденсатору (формула 2):
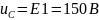
Запишем данные в таблицу 2.
Таблица 2 - Электрические величины в докоммутационном режиме.
i1, i2, i3(0–) |
uR1, uR2, uR3 (0–) |
uC(0–) |
0 |
0 |
0 |
Независимыми начальными значениями являются ток в катушке индуктивности и напряжение на конденсаторе. В нашей схеме присутствует и катушка индуктивности, и конденсатор. Значит, независимым начальным значением будет напряжение на конденсаторе и ток в катушке (формула 3):
Uc = 150 B
Рассчитаем значения в момент коммутации при t = 0+. В момент коммутации ключ S переключается из положения 1 в положение 2 (рис. 1). При этом источник постоянного напряжения Е отключается и подключается источник переменного напряжения e(t).
Конденсатор до коммутации зарядился и имеет полярность. Для упрощения расчетов в момент коммутации конденсатор можно заменить на источник постоянного напряжения или же просто указывать напряжение на конденсаторе. Согласно закону коммутации, напряжение на конденсаторе скачком измениться не может (формула 4):
Uc (0-) = Uc (0+) = 150 B
Пусть ток в цепи будет протекать по часовой стрелке. Составим уравнение по 2 закону Кирхгофа и из него выразим ток в цепи i(0+) (формула 5):
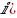
Знак «-» у тока говорит, что на самом деле он протекает в противоположную сторону (против часовой стрелки).
Найдем напряжение на сопротивлении R1 и индуктивность (формула 6, 7):
UR123ком = I1ком ∙ R123 = - 176.597
Запишем данные в таблицу 3.
Таблица 3. Значения электрических величин в момент коммутации.
i1 (0+) |
i2(0+) |
i3(0+) |
uR1(0+) |
uR2(0+) |
uR3(0+) |
uC(0+) |
- 4,816 |
-3,211 |
-1,605 |
-144,488 |
-32,109 |
-32,109 |
150 |
Рассчитаем значения электрических величин в принужденном режиме. Это такой режим, когда ключ S переключился из положения 1 в положение 2 и прошло бесконечно большое время. Расчет напряжений и токов такой электрической цепи выполняется комплексным методом.
Запишем амплитудное комплексное значение напряжения источника ЭДС. (формула 7)

Найдем значение емкостного сопротивления Xc (формула 8):

Найдем амплитудное значение комплексного тока в цепи по закону Ома (формула 9):

Найдем амплитудное комплексное значение напряжения на сопротивлении по закону Ома на 3 резисторах (формула 10):

Найдем амплитудное комплексное значение напряжение на емкости по закону Ома (формула 11):

Запишем данные в таблицу 4.
Таблица 4 - Принужденные значения токов и напряжений.
Комплексные значения в принужденном режиме |
||
Im |
UmR123 |
UmC |
|
|
|
Мгновенные значения в принужденном режиме |
||
iпр(t) |
UR123пр(t) |
UCпр(t) |
0.268∙sin(120t+1.161⁰) |
9.841∙sin(120t+1.161⁰) |
89.46 ∙ sin(120t – 0.41⁰) |
Найдем корни характеристического уравнения. Для этого рассмотрим послекоммутационную схему в свободном режиме. В ней все источники ЭДС заменяются на перемычки, источники тока – на разрывы. Индуктивность заменяется на pL , емкость – 1/pC . В получившейся схеме выполним разрыв любом месте и относительно этого разрыва составим характеристическое сопротивление цепи.
В получившейся электрической цепи два сопротивления подключены последовательно (формула 12):
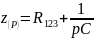
Приравняем характеристическое сопротивление к нулю (формула 48) и найдем неизвестный корень p (формула 13):
P=
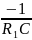
Корень характеристического уравнения отрицательный, значит переходный процесс закончится.
Постоянная времени цепи (формула 14):

Постоянная интегрирования в общем виде рассчитывается (формула 15):
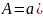
Рассчитаем постоянные интегрирования для тока и напряжений (формулы 15 – 17):



Запишем значения свободных составляющих (формулы 17 – 19):
 А,
А,
 ,
,

Запишем зависимость изменения напряжений и токов от времени при переходном процессе как сумму свободной и принужденной составляющей с учетом значений до коммутации (формулы 17 – 21):
![]()
![]()
![]()
![]()
![]()
Форма графика тока и графика напряжения на сопротивлении совпадает, поэтому график тока строить не будем. Он такой же по форме, как график напряжения на сопротивлении, только в R1 раз меньше. Построим графики напряжений и силы тока на элементах от времени (рисунок 4,5). На 4 рисунке изображен укрупненно момент начала переходного процесса, на рисунке 5 изображена сила тока напряжений на элементах от времени.
Из графиков видно, что выполняется закон коммутации. Напряжение на конденсаторе скачком не изменилось, а ток через конденсатор по форме совпадает с напряжением на резисторе, изменяется скачком.
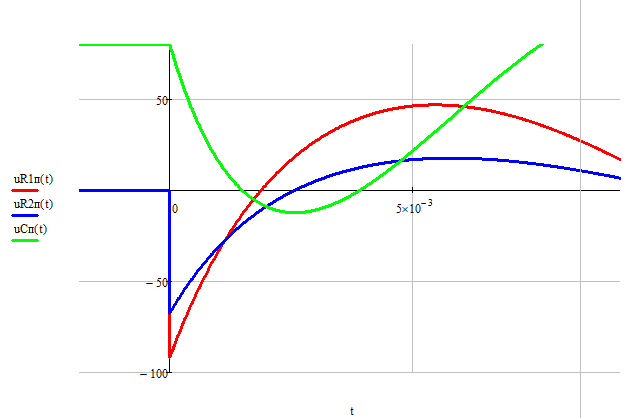
Рисунок 4 - Графики зависимости напряжения на сопротивлении и на емкости от времени.
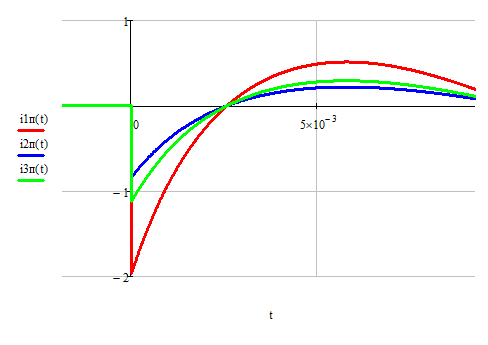
Рисунок 5 - Графики зависимости напряжения на сопротивлении и на емкости от времени на интервале полупериода входного сигнала.
Расчет электрической цепи операторным методом.
Запишем исходные данные расчетной электрической цепи постоянного тока.
Источник входного воздействия задается схемой (рис. 6) и нагрузки (рис. 7):
Рисунок 6 - Источник входного воздействия.
Рисунок 7 – Нагрузка.
Сносим исходные данные в таблицу (табл. 5)
Таблица 5 - Исходные данные
Параметр |
Значение |
R1, Ом/км |
30 |
R1, Ом/км |
10 |
R1, Ом/км |
20 |
L, Гн |
0.6 |
C, мкФ |
25 |
E1, В |
150 |
E2, В |
280 |
Em, В |
90 |
ω, рад/с |
120 |
u, рад |
-0.3 |
Объединим схемы на рисунках и 7 в одну (рис. 8):
Рисунок 8 - Исходная расчетная электрическая цепь.
Проанализируем исходную схему (рис. 8). До коммутации к нагрузке было подключено переменное напряжение e(t). В момент коммутации ключ из положения 1 переключается в положение 2 и 3 на источник постоянного напряжения Е. Через нагрузку начинает протекать постоянный ток.
Найдем докоммутационные значения токов и напряжений. До коммутации источник постоянного напряжения E отключен от цепи, поэтому можно его временно удалить из схемы (рис. 9, 10).
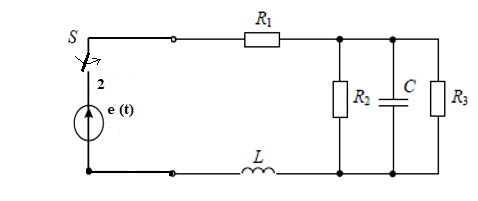
Рисунок 9 - Расчетная электрическая цепь в докоммутационном режиме со 2 ЭДС
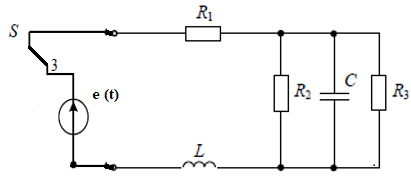
Рисунок 10 - Расчетная электрическая цепь в докоммутационном режиме с 3 ЭДС
Анализ схем (рис. 9,10) показывает, что электрическая цепь содержит всего 3 контур. В этих контурах присутствуют источники переменного напряжения e(t), E1, E2 активных сопротивлений R1, R2, R3 индуктивности L и емкости С. Рассчитаем емкостное сопротивление (формула 22) и индуктивное (формула 23) на переменном токе:

Запишем уравнение по II закону Кирхгофа и выразим из него амплитудное значение комплексного тока в цепи (формула 24):
Запишем уравнение по II закону Кирхгофа и выразим из него амплитудное значение комплексного тока в цепи (формула 25):
Найдем амплитудное комплексное значение напряжения на сопротивлениях по закону Ома до коммутации (формулы 26–28):
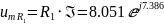 B,
B,

 В.
В.
Комплексные значения токов и напряжений до коммутации |
||||
Im |
UmR1 |
UmC |
UmL |
|
|
|
|
|
|
Мгновенные значения токов и напряжений до коммутации |
||||
i(t) |
0.268∙sin(333.33t+0.246⁰) |
|||
uR1(t) |
8.051∙sin(333.33t+7.386⁰) |
|||
uC(t) |
89.625 ∙ sin(333.33t – 35.692⁰) |
|||
uL(t) |
1.785∙ sin(333.33t – 1.696⁰) |
|||
Значения в момент коммутации t=0- |
||||
i(0-) |
uR1(0-) |
uC(0-) |
uL(0-) |
|
0.247 |
7,386 |
-35.692 |
1.696 |
|
Согласно законам коммутации, в момент коммутации ток через катушку и напряжение на конденсаторе скачком измениться не могут (формулы 29 – 30):
iL (0-) = iL (0+) = -7.734 А,
Uc (0-) = Uc (0+) = -35.692 В.
При выполнении расчетов электрической цепи после коммутации переменные i(t), u(t) замещаются их операторными изображениями I(p), U(p). При переходе от оригинала к изображению источник постоянного напряжения E заменили на его изображение E/P. Индуктивность заменили на последовательное соединение операторного сопротивления p∙L и источник внутренней ЭДС L∙i(0+). Внутреннюю ЭДС L∙i(0+) направили в ту же сторону, куда и ток i(t), протекающий через эту индуктивность. Ёмкость заменили на последовательное соединение операторного сопротивления 1/pS и на источник внутренней ЭДС Uc(0+)/p. Направление внутренней ЭДС Uc(0+)/p противоположно направлению тока через конденсатор.
В результате таких преобразований получилась операторная схема замещения электрической цепи (рис. 11):
Для получившейся схемы составляем уравнение по второму закону Кирхгофа (формула 31):
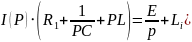
Из уравнения 31 выражаем ток I (p) (формула 32):

Анализируя формулу 32, видим, что степень числителя N(p) ниже степени знаменателя M(p) относительно p. Найдем корни знаменателя
формулы 32. Для этого знаменатель приравняем к нулю и найдем его корни (формулы 33–34):



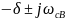
Корни характеристического уравнения получились комплексно- сопряженные, тогда оригинал можно найти по формуле (формула 35):
 ,
,
Где
 можно определить по формуле 36:
можно определить по формуле 36:
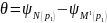 .
.
Объединяем формулу. Получаем конечное выражение для напряжения на конденсаторе (формула 39):
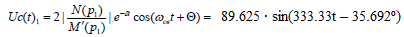
Построим получившиеся графики. Форма тока через все элементы совпадает с напряжением на резисторе, поэтому график тока строить не будем, он в R1 меньше по амплитуде, чем uR1 (t) (рис. 12):
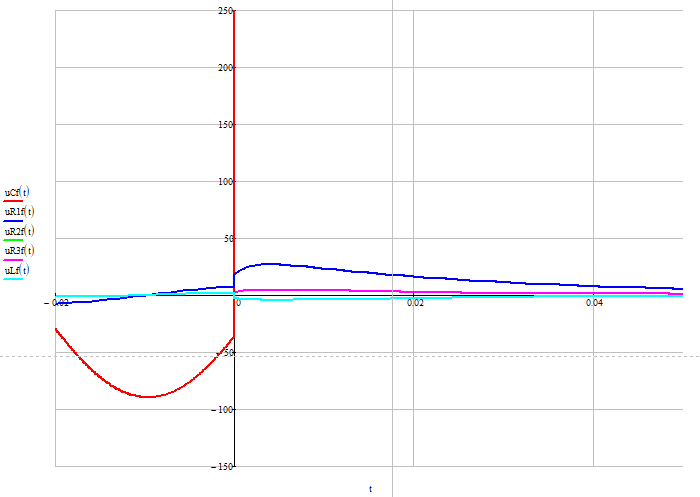
Рисунок 12 - Графики напряжений на элементах
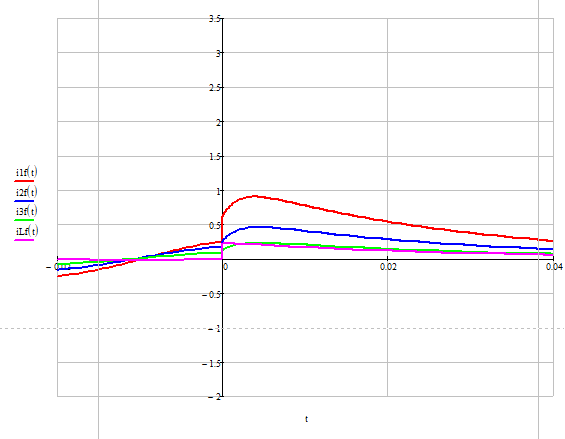
Рисунок 13 - Графики силы тока на элементах
Проанализируем графики. Напряжение на конденсаторе в момент коммутации не изменяется скачком. После окончания переходного процесса напряжение на конденсаторе стремится к напряжению, равному 150 В.
Напряжение на резисторе совпадает по форме с током согласно закону Ома. Этот же ток протекает через катушку индуктивности. Ток через индуктивность в момент коммутации не изменяется скачком. В принужденном режиме ток стремится к нулю.
Напряжение на индуктивности в момент коммутации изменяется скачком, т. к. оно не подпадает по законы коммутации. В установившемся режиме напряжение стремится к нулю.


Воспользуемся
встроенной панелью инструментов «График»
в математическом пакете Mathcad, построим
кривые переходных токов ветвей в
интервале 0˂ t
˂ 5 ∙
 (рис. 14)
(рис. 14)
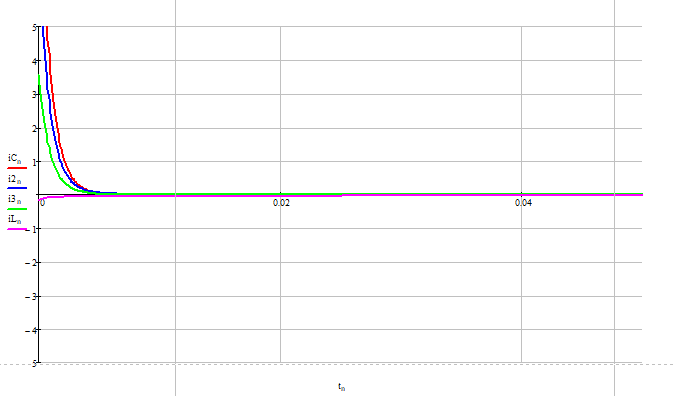
Рисунок 14 - Расчётные переходные токи ветвей

Рисунок 15 - Расчётные переходные напряжения на элементах цепи
амплитудное значение напряжение в переходном процессе на индуктивности превышает в два раза амплитуду напряжения в установившемся режиме. Амплитудное значение напряжения в переходном процессе на конденсаторе превышает амплитуду напряжения в установившемся режиме. Амплитудные значения токов в ветвях с индуктивностью и емкостью превышают амплитуды токов в установившемся режиме.
Вывод:
В данной расчётно-графической работе был определены
Рассчитан переходный процесс классическим методом и определен закон изменения переходных напряжений на каждом элементе расчетной цепи. Рассчитан переходный процесс в линейной электрической цепи с двумя реактивными элементами операторным методом рассчитан переходный процесс в линейной электрической цепи с двумя реактивными элементами методом переменных состояния и сравнен с результатами расчета пунктов, также было замечено, что напряжение на конденсаторе в момент коммутации не изменяется скачком, напряжение на конденсаторе стремится к напряжению, равному 150 В и напряжение на резисторе совпадает по форме с током, так же было замечено, что ток протекает через катушку индуктивности и в момент коммутации не изменяется скачком, но при установившемся режиме напряжение стремится к нулю.

 u,
рад
u,
рад