Практические занятия ЗО

1

Методические указания К паретическим занятиям По дисциплине

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Для студентов заочной формы обучения

2

Практическое занятие №1

ЭЛЕМЕНТЫ КОМБИНАТОРНОГО АНАЛИЗА

Комбинаторные задачи – это задачи, в которых изучаются различного рода соединения (комбинации), составленные из конечного числа элементов по определенному правилу.

Раздел математики, занимающийся решением таких задач, называется

комбинаторикой.

Группы, составленные из каких – либо предметов (элементов) называются соединениями (комбинациями).

Основные правила комбинаторики

Пусть имеется k групп А1, А2, …, Аk, причем i –я группа содержит ni элементов. Тогда справедливы следующие правила.

Правило умножения. Общее число способов N, которыми можно получить упорядоченную совокупность (a1, а2, …, аk), где аi Аi (т.е. выбрать по одному элементу из каждой группы и расставить их в определенном порядке), равно

N = n1 * n2 *…* nk

Задача 1. В группе 30 студентов. Необходимо выбрать старосту, заместителя и профорга. Сколько существует способов такого выбора?

Старостой может быть выбран любой из 30 студентов группы, заместителем – любой из оставшихся 29, а профоргом – любой из оставшихся 28 студентов, т.е. n1 =30, n2 =29, n3 =28. По правилу умножения общее число способов выбора старосты, его заместителя и профорга равно

N = n1 * n2 * n3 = 30 * 29 * 28 = 24360

Задача 2. Два почтальона должны разнести 10 писем по адресам. Сколькими способами они могут распределить работу?

Первое письмо имеет n1 = 2 альтернативы – к адресату его относит либо первый почтальон, либо второй. Для второго и всех последующих писем ni = 2. В силу правила умножения общее число способов распределения писем между двумя почтальонами равно

N = n1 * n2 *…* n10 = 2*2*2*2*2*2*2*2*2*2 = 210 =1024

Правило сложения. Если один элемент из группы Аi можно выбрать ni способами и при этом любые две группы Аi и Аj не имеют общих элементов, то выбор одного элемента или из А1, или из А2, …, или из Аk можно осуществить N способами:

N = n1 + n2 +…+ nk

3

Задача 3. В ящике 100 деталей, из них 30 – первого сорта, 50 – второго, остальные – третьего. Сколько существует способов извлечения из ящика одной детали первого или второго сорта?

Деталь первого сорта может быть извлечена n1 = 30 способами, второго сорта – n2 =50 способами. По правилу суммы существует N = n1 + n2 = 30 +50 = 80

способов извлечения одной детали первого или второго сорта.

Основные формулы комбинаторики (перестановки, размещения, сочетания)

Упорядоченные совокупности (перестановки и размещения) –

последовательный выбор.

Неупорядоченные совокупности (сочетания) – одновременный выбор.

Комбинации без повторений – отобранный элемент не возвращается в генеральную совокупность; все n элементов различны.

Комбинации с повторениями – отобранный элемент перед отбором следующего возвращается в генеральную совокупность; некоторые элементы могут повторяться.

Представьте, что перед вами на столе материализовалось яблоко, груша и банан. Выкладываем фрукты слева направо в следующем порядке:

яблоко / груша / банан Вопрос первый: сколькими способами их можно переставить?

Одна комбинация уже записана выше и с остальными проблем не возникает:

яблоко / банан / груша груша / яблоко / банан груша / банан / яблоко банан / яблоко / груша банан / груша / яблоко

Итого: 6 комбинаций или 6 перестановок.

Вданном случае применима формула перестановок, поскольку определяем

:«Сколькими способами можно переставить n объектов?»

Никаких мучений – 3 объекта можно переставить способами. Вопрос второй: сколькими способами можно выбрать а) один фрукт, б)

два фрукта, в) три фрукта, г) хотя бы один фрукт?

а) Один фрукт можно выбрать, очевидно, тремя способами – взять либо яблоко, либо грушу, либо банан. Формальный подсчёт проводится очевидно рассчитывается п формуле сочетаний, т.е.

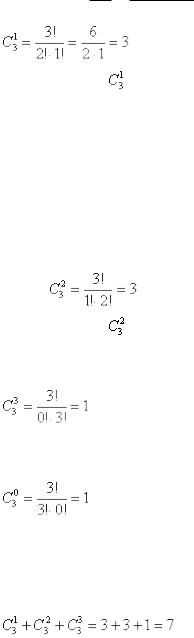
4

«Сколькими способами можно выбрать m объектов из n ?». Поскольку выборка проводится из множества, состоящего из n объектов, то справедливо неравенство 0 m n

Запись в данном случае следует понимать так: «сколькими способами можно выбрать 1 фрукт из трёх?»

б) Перечислим все возможные сочетания двух фруктов: яблоко и груша; яблоко и банан; груша и банан.

Количество комбинаций легко проверить по той же формуле:

Запись понимается аналогично: «сколькими способами можно выбрать 2 фрукта из трёх?».

в) И, наконец, три фрукта можно выбрать единственным способом:

Кстати, формула количества сочетаний сохраняет смысл и для пустой выборки:

способом можно выбрать ни одного фрукта – собственно, ничего не

взять и всё.

г) Сколькими способами можно взять хотя бы один фрукт? Условие «хотя бы один» подразумевает, что нас устраивает 1 фрукт (любой) или 2 любых фрукта или все 3 фрукта:

способами можно выбрать хотя бы один фрукт.

Тут возможно суммирование, поскольку надо вытянуть или1 или2 или 3 фрукта.

Вопрос третий: сколькими способами можно раздать по одному фрукту Даше и Наташе?

Т.е надо вытянуть два фрукта и раздать Наташе и Даше

просто вытащить два фрукта из трех можно способами, перепишу их заново:

яблоко и груша; яблоко и банан; груша и банан.

6

исключить. Пусть ноль находится на 1-м месте, тогда оставшиеся 3

цифры в младших разрядах можно переставить способами. Таким образом, из предложенного набора можно составить:

24 – 6 = 18 четырёхзначных чисел

Ответ: 18

Перестановки с повторениями

В перестановках с повторениями, как и в «обычных» перестановках, участвует сразу всё множество объектов, но есть одно но: в данном множестве один или бОльшее количество элементов (объектов) повторяются.

Задача 3

Сколько различных буквосочетаний можно получить перестановкой карточек со следующими буквами: К, О, Л, О, К, О, Л, Ь, Ч, И, К?

Решение: в том случае, если бы все буквы были различны, то

следовало бы применить тривиальную формулу , однако совершенно понятно, что для предложенного набора карточек некоторые манипуляции будут срабатывать «вхолостую», так, например, если поменять местами любые две карточки с буквами «К» в любом слове, то получится то же самое слово..

Всё предельно просто – всего: 11 карточек, среди которых буква: К – повторяется 3 раза; (к1)

О – повторяется 3 раза; (к2) Л – повторяется 2 раза; (к3) Ь – повторяется 1 раз; (к4)

Ч – повторяется 1 раз; (к5) И – повторяется 1 раз. (к6)

Проверка: 3 + 3 + 2 + 1 + 1 + 1 = 11, что и требовалось проверить.

различных буквосочетаний можно получить. Больше полумиллиона!

Для быстрого расчёта большого факториального значения удобно использовать стандартную функцию Экселя: забиваем в любую ячейку =ФАКТР(11) и жмём Enter.

На практике вполне допустимо не записывать общую формулу и, кроме того, опускать единичные факториалы:

Но предварительные комментарии о повторяющихся буквах обязательны!

Ответ: 554400

7

Размещения

Размещения без повторений. Отобранный элемент перед отбором следующего не возвращается в генеральную совокупность. Такой выбор называется размещением k элементов из n, или последовательным выбором без возвращения.

Размещения – это упорядоченные совокупности k элементов из n, отличающиеся друг от друга либо составом, либо порядком элементов. Общее число способов размещения k элементов из n определяется по формуле

Задача 5

Боря, Дима и Володя сели играть в «очко». Сколькими способами им можно сдать по одной карте? (колода содержит 36 карт)

Решение: здесь важно не только то, какие три карты будут извлечены из колоды, но и то, КАК они будут распределены между игроками. По формуле размещений:

способами можно раздать 3 карты игрокам. Есть и другая схема решения, которая, с моей точки зрения,

даже понятнее:

Найдем с помощью сочетания возможность выбора 3 карт из 36

способами можно извлечь 3 карты из колоды. Теперь 3 карты надо перераспределить между Борей, Димой и

Володей способами: И тогда справедливо:

способами можно сдать по одной карте трём игрокам.

Ответ: 42840

Задача 6

В студенческой группе 23 человека. Сколькими способами можно выбрать старосту и его заместителя?

Решение: способами.

Другой вариант решения: способами можно выбрать двух

человек из группы и способами распределить должности в каждой выборке. Таким образом, старосту и его заместителя можно

выбрать способами.

Ответ: 506

8

Размещения с повторениями

Из множества, состоящего из n элементов, выбирается k элементов, при этом важен порядок элементов в каждой выборке. И всё бы было ничего, но довольно неожиданный прикол заключается в том, что любой объект исходного множества мы можем выбирать сколько угодно раз. Или иначе, отобранный элемент перед отбором следующего возвращается в генеральную совокупность

Задача 7. Имеется 6 флажков разного цвета. Сколько из них можно составить сигналов, если первый флажок после сигнала возвращается в генеральную совокупность флажков, затем отбирается второй.

Задача 8. Байт – единица информации, состоящая из 8 бит, каждый бит равен либо 0, либо 1. Сколько символов можно закодировать с помощью байта.

Сочетания

Сочетаниями называют различные комбинации из k объектов, которые выбраны из множества n различных объектов, и которые отличаются друг от друга хотя бы одним объектом. Иными словами, отдельно взятое сочетание – это уникальная выборка из k элементов, в которой не важен их

порядок (расположение). Общее же количество таких уникальных сочетаний

рассчитывается по формуле .

Задача 9

В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?

Решение: прежде всего, снова обращаю внимание на то, что по логике условия, детали считаются различными – даже если они на самом деле однотипны и визуально одинаковы (в этом случае их можно,

например, пронумеровать).

В задаче речь идёт о выборке из 4 деталей, в которой не имеет значения их «дальнейшая судьба» – грубо говоря, «просто выбрали 4 штуки и всё». Таким образом, у нас имеют место сочетания деталей. Считаем их количество:

способами можно

взять 4 детали из ящика.

9

Ещё раз: что это значит? Это значит, что из набора 15 различных деталей можно составить одну тысячу триста шестьдесят пять уникальных сочетания 4 деталей. То есть, каждая такая

комбинация из четырёх деталей будет отличаться от других комбинаций хотя бы одной деталью.

Ответ: 1365 способами

Формуле необходимо уделить самое пристальное внимание, поскольку она является «хитом» комбинаторики. При этом полезно ПОНИМАТЬ и без всяких вычислений записывать «крайние»

значения: . Применительно к разобранной задаче:

– единственным способом можно не выбрать ни одной детали;

способами можно взять 1 деталь (любую из пятнадцати);

способами можно взять 14 деталей (при этом какая-то одна из 15 останется в ящике);

– единственным способом можно взять все пятнадцать деталей.

Задача 10

Сколькими способами из колоды в 36 карт можно выбрать 3 карты?

Решение: способами можно выбрать 3 карты из 36.

Ответ: 7140

Задача 11 В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми участниками должна быть сыграна одна партия?

Решение Каждая партия играется двумя участниками из 16 и отличается от

других только составом пар участников, т.е. представляет собой сочетания из 16 элементов по 2. Их число равно

Сочетания с повторениями

Характерная особенность этого вида комбинаций состоит в том, что выборка проводится из нескольких групп, каждая из которых состоит из одинаковых объектов.

Задача 12

В кошельке находится достаточно большое количество 1-, 2-, 5- и 10рублёвых монет. Сколькими способами можно извлечь три монеты из кошелька?

10

: Решение: используем формулу сочетаний с повторениями:

способами можно выбрать 3 монеты из кошелька.

Ответ: 20

Домашнее задание

1.Три наборщика должны набрать 20 страниц текста. Сколько существует способов распределения работы между ними.

2.С цифр 1,2,3,4,5 составляют разные трехзначные и четырехзначные числа. Сколько таких чисел можно сложить, если повторение цифр в числах:

а) запрещено; б) возможно.

3.Сколькими способами можно разместить 12 гостей за столом, возле которого стоят

12 стульев.

4.Сколько существует пятизначных чисел, состоящих из цифр 1, 3 в которых цифра 1 повторяется 3 раза, цифра 3 - 2 раза?