Лекция 3

Лекция 3

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛП

Решить задачу линейного программирования – означает найти такие значения переменных, которые удовлетворяют всем ограничениям, а ЦФ достигает искомого экстремума.

Определение 1. Значения неизвестных переменных, удовлетворяющие всем ограничениям задачи линейного программирования, называются допустимыми значениями переменных или планами.

Определение 2. Множество всех планов задачи линейного программирования называется областью допустимых значений переменных (ОДЗ).

Определение 3. План задачи линейного программирования, при котором целевая функция принимает минимальное (или максимальное) значение на ОДЗ называется оптимальным.

Геометрическая интерпретация задач ЛП, позволяет наглядно представить их структуру и выявить их особенности. Задачу ЛП с двумя переменными всегда можно решить графически. Однако в трехмерном пространстве такое решение существенно усложняется, а в пространстве размерность которого больше трех, графическое решение , вообще говоря, невозможно.

Рассмотрим математическую модель общей задачи ЛП в стандартной форме:

Z=c₁x₁+c₂x₂ – max (1)

при ограничениях: a₁₁x₁ + a₁₂x₂ ≤ b₁

a₂₁x₁ + a₂₂x₂ ≤ b₂

– – – – – – (2)

a_m1x₁ + a_m2x₂ ≤ b_m

x₁, x₂ ≥ 0 (3)

Необходимо найти план (точку) X (x1, x2 ) , в которой целевая функция принимает максимальное значение.

Дадим геометрическую интерпретацию элементов этой задачи. Выполнить геометрическую интерпретацию задачи ЛП означает поставить в соответствие каждой части математической модели задачи (целевой функции, системе ограничений, условию неотрицательности) - геометрические образы.

В качестве системы координат возьмем систему координат ХОУ.

Оси Ox ( абсцис) и Oy (ординат) соответственно примем Ox₁ и Ox₂ , а систему координат x₁O x_{2 .}

Условие неотрицательности переменных (3) x₁,x₂ ≥ 0, геометрическим образом является 1-я четверть плоскости.

Геометрическим образом линейного уравнения с двумя неизвестными является прямая

Геометрическим образом линейного неравенства является одна из 2-х полуплоскостей, на которые соответствующая прямая делит всю плоскость x₁Ox₂.

Чтобы определить координаты точек какой полуплоскости, удовлетворяющие заданному неравенству, нужно в левую часть неравенства подставить координаты какой-нибудь точки, лежащей в одной из полуплоскостей. Удобно взять координаты начала – т. (0,0). Если координаты взятой точки удовлетворяют неравенству, то ему будут удовлетворять координаты всех точек, расположенных в той же полуплоскости, что и взятая точка.

Поэтому, чтобы получить геометрический образ системы структурных ограничений (2), необходимо построить прямые (=), соответствующие каждому структурному ограничению:

a₁₁x₁ a₁₂ x₂  b₁

a₂₁x₁ a₂₂ x₂  b₂ (4)

a_m1x₁ a_m2 x₂ b_m

Каждое линейное уравнение a_i1x₁ a_{i 2} x₂ b_i , (i 1,m), в системе уравнений (4),определяет на плоскости x₁Ox₂прямую линию. Каждое неравенство системы (3), есть соответствующая полуплоскость.

Геометрическим образом системы неравенств (структурных ограничений) (2) и условия неотрицательности (3), является общая часть полуплоскостей (многоугольник) расположенная в 1-ой четверти плоскости.

Рассмотрим задачу: max{F(x)= c₁x₁+ c₂x₂|( a_j1x₁+ a_j2x₂)≥(≤)b_j,j=1,m; x₁≥0, x₂≥0}.

Каждое из ограничивающих неравенств определяет полуплоскость, лежащую по одну сторону прямой a (a_j1x₁+ a_j2x₂)=b_j , j = 1,m. ОДЗП получится в результате пересечения m полуплоскостей. Условия неотрицательности позволяют ограничиться рассмотрением положительного квадранта.

На рис. 1 показан один из возможных вариантов ОДЗП в виде замкнутого многоугольника для случая m = 3.

Рисунок 1 - Графическая интерпретация задачи линейного программирования

Координаты x₁ и x₂ любой точки, принадлежащей области, удовлетворяют системе ограничений задачи линейного программирования. Чтобы найти оптимальное решение, зададим функции цели некоторое постоянное значение F₁ = c₁x₁ + c₂x₂ = const и построим прямую F₁, которая будет отсекать на оси ординат (x₁ = 0) отрезок , x₂=F₁/c₂ а на оси абсцисс (x₂=0) – отрезок x₁=F₁/c₁. Если задать другие значения функции цели F₂ , F₃ ,... и изобразить соответствующие линии, то получим семейство параллельных прямых, которые называются линиями уровня функции цели. Направление стрелки показывает направление увеличения целевой функции F₁ < F₂ < F₃ < .... Величину функции цели можно характеризовать расстоянием d от начала координат до линии уровня в соответствии с выражением d=(F₁/F₂)cosα.

В теории линейного программирования доказано, что если оптимальное решение задачи линейного программирования существует и единственно, то оно достигается в некоторой вершине многоугольника решений. Очевидно, что целевая функция достигает максимального значения тогда, когда её линия будет проходить через точку M. Координаты этой точки будут оптимальным решением задачи. Минимальное значение рассматриваемой функции будет достигаться в начале координат. Таким образом, если требуется определить такие x₁ и x₂, которые обеспечивают максимум функции цели, то геометрически это означает, что необходимо провести прямую F = const , проходящую хотя бы через одну вершину области и имеющую максимальное расстояние d от начала координат.

В случае минимизации это расстояние должно быть минимальным. В зависимости от вида ОДЗП и расположения линий уровня могут встретиться случаи, изображенные на рис. 2.

Рис. 2 - Различные варианты решения задач линейного программирования

На рис.2, а функция F достигает минимума в начале координат. При максимизации функции ее линия совпадает со стороной ВС, ограничивающей ОДЗП. Координаты любой точки отрезка ВС будут доставлять максимум функции F, что соответствует бесчисленному множеству оптимальных решений задачи линейного программирования.

На рис. 2, б ОДЗП не замкнута, целевая функция сверху не ограничена, т.е. максимального значения не имеет. Минимальное значение функция принимает в точке A.

На рис. 2, в приведен случай несовместных ограничений, в этом случае функция цели не имеет ни максимума, ни минимума, так как ОДЗП представляет собой пустое множество.

Совокупность любого числа линейных ограничений выделяет в пространстве x₁, x₁,..., x_n некоторый выпуклый многогранник, ограничивающий область допустимых значений переменных (ОДЗП).

Особенности решения задач ЛП тесно связаны с особенностями выпуклых множеств.

Вначале дадим некоторые определения.

Определение 1. Множество точек называется выпуклым, если вместе с его любыми двумя точками ему принадлежит и весь отрезок, соединяющий их.

На рис. 3.1 изображено выпуклое множество (выпуклый многоугольник), а на рис. 3.2 - невыпуклое.

рис. 3.1	рис. 3.2

Определение 2. Пересечение конечного числа выпуклых множеств также выпуклое множество.

Определение 3. Точка выпуклого множества называется угловой (или крайней), если через неё нельзя провести ни одного отрезка, состоящего только из точек данного множества и для которого она была бы внутренней.

Для выпуклого многоугольника угловыми точками являются все его вершины. В пространстве выпуклое множество с конечным числом угловых точек называется выпуклым многогранником.

Утверждение 1. Множеством решений системы m линейных неравенств с n переменными является выпуклый многогранник в n-мерном пространстве (исключая случай, когда система несовместна).

Теорема 1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.

Ранее говорилось, что ограничениями любой задачи линейного программирования являются либо система линейных уравнений, либо система линейных неравенств. Совокупность решений таких систем при условии их совместности, образует выпуклые множества с конечным числом угловых точек. В частном случае, когда в систему ограничений - неравенств входят только две переменные x₁ и x₂ это множество можно изобразить на плоскости.

Рассмотрим систему линейных неравенств с двумя неизвестными:

a₁₁x₁ + a₁₂x₂ ≤ b₁

a₂₁x₁ + a₂₂x₂ ≤ b₂

– – – – – –

a_m1x₁ + a_m2x₂ ≤ b_m

Каждое из неравенств этой системы на плоскости определяет полуплоскость.

Система линейных неравенств называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

Решением системы линейных неравенств называется любая пара чисел (x₁ ; x₂ ), удовлетворяющая всем неравенствам данной системы.

Геометрически решением системы линейных неравенств является множество точек, удовлетворяющих всем неравенствам системы, то есть, общая часть получаемых полуплоскостей. Поэтому геометрически в общем случае решение может быть изображено в виде некоторого многоугольника, в частном случае - может быть линия, отрезок и даже точка. Если система линейных неравенств несовместна, то на плоскости не существует ни одной точки, удовлетворяющей всем неравенствам системы.

Теорема 2. Если задача линейного программирования имеет оптимальное решение, то оно совпадает с одной (двумя) из угловых точек множества допустимых решений.

Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых решений системы ограничений, и наоборот.

Схема решения задач линейного программирования графическим методом:

1. Построить многоугольник решений системы неравенств.

2. Начертить из семейства прямых, соответствующих линейной форме, линию равных значений функции цели. Для построения линии равных значений придадим F некоторое числовое значение. Во многих задачах удобно принять, что F =1. Тогда получим  . Запишем это уравнение прямой в отрезках:

Затем, откладывая на оси   число  , а на оси   - число  , найдём точки пересечения линии равных значений с осями координат. Прямая, проведённая через эти точки, и есть требуемая прямая.

3. Двигать прямую (или линейку) вдоль градиента - вектора   параллельно линии равных значений в сторону многоугольника решений до соприкосновения с многоугольником решений. Если первая встреча с многоугольником решений произойдёт в крайней точке с координатами  , то в этой точке функция цели достигает минимального значения. Если первая встреча произойдёт со стороной многоугольника, то данная функция цели достигает минимума во всех точках этой стороны.

4. Двигаясь дальше, придём к некоторому опорному положению, когда прямая будет иметь одну общую точку   с многоугольником решений. В этой точке функция цели достигает своего максимума.

5. Если первоначально построенная линия равных значений пересекает многоугольник решений, то функция цели достигает минимального значения в вершине многоугольника, расположенной ближе к началу координат, а максимального значения - в вершине, более удалённой от начала координат.

Пример решения задачи графическим методом

Задача. Для изготовления столов и шкафов используется два вида древесины: Д₁ и Д₂. На изготовление одного шкафа необходимо 0,2м³  древесины  Д₁ и   0,1м³  древесины Д₂. На изготовление одного стола нужно  0,15м³  древесины  Д₁и  0,2м³  древесины Д₂. Доход мастерской от реализации одного стола составляет -12 ден. ед., а одного шкафа - 15 ден. ед. Определить, сколько столов и сколько шкафов необходимо изготовить , чтобы обеспечить наибольший доход, если в распоряжении мастерской имеется древесины  Д₁ - 60 м³, а древесины Д₂ - 40м³.

Необходимо записать экономико-математическую модель задачи.

Вид древесины	Вид изделия
	стол	шкаф	запасы
Д1	0,15	0,2	60
Д2	0,2	0,1	40
Доход	12	15

В качестве параметров управления выберем:

Х₁ - количество столов  ,а количество шкафов – Х₂.

Тогда из таблицы легко составить систему ограничений :

и целевую функцию:

, которая стремится к max.

Для удобства, преобразуем неравенства , умножив на 100. Получим

,

где

.

Сокращая первое неравенство на 5, а второе на 10, получим

Далее, для упрощения вычислений введём масштаб 1:100, то есть, в правых частях последней системы неравенств отбросим по два нуля, тогда система запишется в ви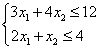де

,где

, найти  .

Дальнейшее решение задачи ведётся по схеме, изложенной выше.

Строим многоугольник решений системы. Для этого построим на координатной плоскости прямые, заданные уравнениями системы. Для этого надо знать какие-либо две точки этой прямой. Ищем точки пересечения каждой прямой с осью абсцисс, подставляя значение   в соответствующее уравнение. Затем ищем точки пересечения каждой прямой с осью ординат, поставляя значение  . Ясно, что решениями системы могут быть только положительные решения. Поэтому многоугольником решений будет четырёхугольник  . Теперь ищем значение максимума функции цели. Линейная форма   геометрически означает семейство параллельных между собой прямых. Среди прямых этого семейства есть опорные прямые mn и MN. Это такие прямые, которые имеют с многоугольником хотя бы одну точку и многоугольник целиком лежит по одну сторону от этой прямой. Как видно из рисунка, прямая mn является опорной, так как она касается многоугольника в точке О и многоугольник целиком лежит правее (или выше) этой прямой. Прямая MN также является опорной, так как имеет с многоугольником общую точку В и многоугольник целиком лежит левее (или ниже) этой прямой. Из рисунка видно, что функция цели достигает максимума в точке B (80, 240) (не забываем про масштаб). Подставляя координаты точки в функцию цели, имеем

.

Таким образом, максимум дохода в сумме 4560 ден. ед. мастерская получит, если изготовит 80 столов и 240 шкафов.

9