
573
.pdf
а) |
б) |
в) |
г)
Рис. 6.2. Примеры колебательных систем
Как и следовало ожидать, эти величины не зависят от массы груза, амплитуды колебаний и способа возбуждения колебаний. Они определяются только длиной маятника (чем больше длина маятника, тем больше период) и ускорением свободного падения g.
Стоит обсудить вопрос об энергии колебаний. Рассмотрим этот вопрос снова на примере колебаний пружинного маятника. Полная энергия колебаний такого маятника будет складываться из кинетической энергии движения груза и потенциальной энергии упругой деформации, запасенной в пружине:
E = |
mv2 |
+ |
kx2 |
= |
mω2 |
A2 |
= |
kA2 |
|
|
|
|
0 |
|
|
. |
(6.7) |
||||
2 |
2 |
2 |
|
2 |
||||||
|
|
|
|
|
|
|
||||
Скорость груза v легко определить, воспользовавшись формулой (6.4):
v= dx = −Aω0 sin(ω0t + ϕ0 ) . dt
Подставляя это выражение и выражение (6.4) в формулу (6.7), получаем:
|
|
|
|
|
m |
2 |
2 |
2 |
|
|
|
|
|
k |
2 |
2 |
|
|
|
|
|
|
|
||
|
E = |
|
|
A |
ω |
sin |
(ω t + ϕ |
) + |
|
|
A |
cos |
(ω t |
+ ϕ |
) = |
|
|||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
2 |
|
|
0 |
|
0 |
|
0 |
|
|
2 |
|
|
|
|
0 |
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
m |
|
A2ω2 sin2 (ω t + ϕ |
) + |
mω2 |
A2 cos2 (ω t + ϕ |
|
) = |
|
||||||||||||||||
|
|
|
0 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
2 |
|
|
0 |
|
|
0 |
0 |
|
|
2 |
|
|
|
|
0 |
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
mω2 A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mω2 |
A2 |
|||||||
= |
|
|
|
0 |
|
[sin2 (ω t + ϕ |
) + cos2 (ω t + ϕ |
)] = |
|
|
0 |
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
|
|
0 |
0 |
|
|
|
|
|
0 |
|
0 |
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Полная энергия колебаний, таким образом, является постоянной величиной и пропорциональна квадрату амплитуды колебаний:
E = |
mω2 A2 |
= |
kA2 |
|
|
0 |
|
. |
(6.8) |
||
|
|
||||
22
Этот результат оказывается справедливым не только для пружинного маятника, но для общего случая колебаний (любой природы). Зависимости основных величин, описывающих процесс, от времени приведены на рис. 6.3.
43

Рис. 6.3. Зависимости от времени физических характеристик колебательной системы (например, пружинного маятника): x — смещение; v — скорость; а — ускорение; K — кинетическая энергия;
W — потенциальная энергия
Коротко рассмотрим еще одну колебательную систему — колебательный контур, состоящий из двух элементов: конденсатора и катушки индуктивности. Первоначально заряжается конденсатор, затем цепь замыкается и в контуре происходит периодический процесс перезарядки конденсатора. На рис. 6.4 приведены пять состояний колебательного контура через четверть периода по времени. Допустим, что при t = 0 одна пластина (верхняя) конденсатора заряжена зарядом +q, другая, соответственно, имеет заряд –q, заряженный конденсатор обладает энергией электростатического поля, которое сосредоточено между его обкладками. Так как цепь в этот момент замкнули, заряд начал перетекать по контуру, через катушку потек электрический ток, в катушке возникло магнитное поле, накапливается энергия магнитного поля. В момент времени t = 0,25Т (T — период колебания) конденсатор разрядился, но ток продолжает течь, конденсатор заряжается (полярность противоположная), при этом энергия магнитного поля катушки переходит в энергию электростатического поля конденсатора. В момент времени t = 0,5Т наблюдается следующая картина: верхняя пластина конденсатора заряжена зарядом –q, другая, соответственно, имеет заряд +q, есть энергия заряженного конденсатора, ток не течет, энергия магнитного поля катушки равна нулю. Далее возникает ток в обратном направлении, энергия магнитного поля катушки растет и достигает максимальной величины в момент времени t = 0,75Т, при этом конденсатор полностью разряжен. Далее идет процесс зарядки конденсатора до исходного состояния: верхняя пластина +q, нижняя пластина –q, это наступает при t = 1Т. Рассмотренные стадии процесса, происходящего в колебательном контуре, можно сопоставить с соответствующими состояниями математического маятника. На рис. 6.4 под изображением каждого состояния колебательного контура приведено соответствующее состояние математического маятника. Энергия заряженного конденсатора соответствует потенциальной энергии маятника, а энергия магнитного поля катушки соответствует кинетической энергии маятника. Период колебания колебательного контура выражается через параметры контура:
|
|
|
|
T = 2π LC . |
(6.9) |
||
Рис. 6.4. Аналогия процессов в колебательном контуре с процессами, происходящими при колебаниях математического маятника
44
6.2. Затухающие колебания
Если на систему, совершающую колебания, будут действовать силы трения, то с течением времени колебания будут затухать. Затухающими колебаниями, таким образом, можно назвать колебания системы, на которую кроме возвращающей силы действуют силы трения. Уравнение, описывающее затухающие колебания, снова получим на примере пружинного маятника. Для этого учтем силу сопротивления среды Fc = −bv , действующую на маятник, которая пропорциональна
скорости его движения v:
a = − |
k |
x − |
b |
v |
(6.10) |
|
|
||||
|
m m |
|
|||
(сравните с (6.2)), и выразим ускорение а и скорость v грузика как производные от координаты x, тогда получим уравнение:
d2 x |
+ 2δ |
dx |
+ ω2x = 0 . |
(6.11) |
|
dt2 |
dt |
||||
|
0 |
|
Уравнение (6.11) описывает затухающие колебания любой природы и называется дифференциальным уравнением затухающих колебаний. Коэффициент δ в этом уравнении называют коэффи-
циентом затухания: δ = b . Коэффициент затухания δ связан с коэффициентом b,
2m
т.е. определяется свойствами среды, в которой совершаются колебания: чем больше δ , тем больше сила сопротивления, оказываемая средой при одной и той же скорости движения. На рис. 6.5, а показана схема пружинного маятника с трением, здесь указана сумма всех сил трения и сопротивления. Выбор зависимости силы сопротивления от скорости (Fc =
= –bv) позволяет решить уравнение (6.11). Решение уравнения (6.11) имеет вид:
x = A e−δt cos(ωt + ϕ |
) , |
(6.12) |
|||
0 |
|
0 |
|
|
|
где циклическая частота равна |
|
|
|
|
|
|
|
|
|
|
|
ω = |
ω 2 |
− δ2 . |
|
(6.13) |
|
|
0 |
|
|
|
|
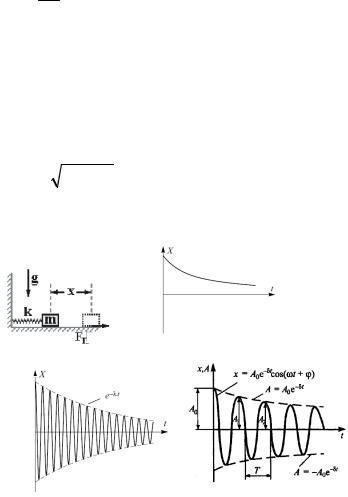
График этого решения изображен на рис. 6.5, в, г.
б)
а)
в) |
г) |
|
|
Рис. 6.5. Затухающие колебания
Из (6.12) видно, что действие сил сопротивления среды приводит к экспоненциальному затуханию амплитуды колебаний со временем (рис. 6.5, б), и тогда смещение равно произведению экспоненты на
синусоиду (рис. 6.5, в). Амплитуда колебания зависит от времени по закону: A = A0e−δt . Величина,
равная отношению амплитуды в момент времени t к амплитуде в момент времени t + T, т.е. через период, называется декрементом затухания, а ее натуральный логарифм — логарифмическим декре-
45

ментом затухания. Полная механическая энергия затухающих колебаний экспоненциально уменьша-
ется с течением времени: E = mω2 A02 e−2δt и переходит в тепло. Из формулы (6.13) видно, что коле-
2
бания возникают не во всякой среде, а только в том случае, когда δ < ω0 . В случае же достаточно плотной, вязкой среды (например, очень вязкое плотное масло), когда δ ≥ ω0 , колебания невозможны. Интересным случаем движения маятников является случай, когда δ = ω0 . В этом случае ω = 0, а x = A0e−δt cosϕ0 , т.е. выведенный из равновесия маятник просто плавно возвращается в положение равновесия и останавливается.
6.3. Вынужденные колебания. Резонанс.
Параметрический резонанс
Рассмотрим теперь более сложный случай колебаний под действием внешней силы F(t), величина которой изменяется со временем. Такие колебания называются вынужденными колебаниями (рис. 6.6).
а)
б)
в)
г)
д)
е)
Рис. 6.6. Вынужденные колебания:
а— рост амплитуды вынужденного колебания; б, в — вынуждающие силы;
г— зависимость конечной амплитуды от частоты вынуждающей силы;
д— с начала действия вынуждающей силы амплитуда растет до определенного уровня, зависящего от сил сопротивления; е — амплитуда резонанса растет
суменьшением коэффициента затухания
Мы ограничимся наиболее интересным случаем периодической внешней силы. Сила зависит от времени по гармоническому закону, F0 — амплитуда приложенной силы; ωF — частота вынуждающей силы:
(6.14)
Уравнение, описывающее такие колебания, с учетом сопротивления среды будет иметь вид:
d2 x |
+ 2δ |
dx |
+ ω2 x = |
F |
cos(ω |
|
|
|
|
|
0 |
t) , |
(6.15) |
||||
dt2 |
dt |
m |
||||||
|
0 |
F |
|
|
а его решение, по прошествии достаточно большого времени от начала колебаний, имеет вид:
|
x ≈ Acos(ωFt) , |
|
|
(6.16) |
|||
где амплитуда колебаний равна: |
|
|
|
|
|||
A = |
|
|
F0 |
m |
|
. |
(6.17) |
|
|
|
|
|
|||
|
|
(ω2 |
− ω2 |
)2 + 4δ2 |
ω2 |
|
|
0 |
F |
|
F |
|
|||
Как видно из рис. 6.6, а и формулы (6.16), по прошествии некоторого времени устанавливаются колебания с частотой, равной частоте ωF воздействия внешней силы. Амплитуда этих колебаний определяется амплитудой F0 внешней силы, коэффициентом затухания δ и соотношением частот ωF и ω0
46
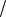
(рис. 6.6, д, е). При этом потери энергии на нагревание окружающей среды компенсируются поступлением энергии от внешнего источника вынуждающей силы. Таким образом, полная энергия установившихся колебаний не меняется. Особенно интересным случаем вынужденных колебаний под действием периодической силы является случай, когда частота вынуждающей силы близка к частоте собственных колебаний: ωF ≈ ω0 . В этом случае резонансная амплитуда установившихся колебаний
(6.17) в значительной степени зависит от коэффициента затухания среды δ и может достигать очень больших значений, если этот коэффициент достаточно мал, причем, независимо от амплитуды вынуждающей силы:
A = lim |
F0 m |
→ ∞ . |
(6.18) |
||
2δω |
|||||
ðåç |
δ→0 |
|
|
||
|
|
|
|
||
F
Явление резкого возрастания амплитуды вынужденных колебаний (рис. 6.6, е) при совпадении частоты вынуждающей силы с собственной частотой системы, способной совершать колебания, называется резонансом.
Явление резонанса важно потому, что оно проявляется достаточно часто. С резонансом сталкивался каждый, кто раскачивал, например, ребенка на качелях. Это довольно трудно сделать, если закрыть глаза и беспорядочно толкать качели. Но если найти правильный ритм, то раскачать качели легко. Наибольшего результата, таким образом, можно достичь лишь тогда, когда время между отдельными толчками будет совпадать с периодом колебаний качелей, т.е. выполняется условие резонанса. С явлением резонанса приходится считаться при конструировании машин и различного рода сооружений. Собственная частота колебаний этих устройств ни в коем случае не должна быть близка к частоте возможных внешних воздействий. Так, например, собственная частота вибраций корпуса корабля или крыльев самолета должна сильно отличаться от частоты колебаний, которые могут возбуждаться при вращении гребного винта корабля или пропеллера самолета. В противном случае возникают вибрации большой амплитуды, которые могут привести к разрушению обшивки и катастрофе. Известны случаи, когда обрушивались мосты при прохождении по ним марширующих колонн солдат. Это происходило потому, что собственная частота колебаний моста оказывалась близкой к частоте, с которой шагала колонна (рис. 6.7).
Вместе с тем явление резонанса часто оказывается весьма полезным. Благодаря резонансу, например, стало возможным использование ультразвуковых колебаний, т.е. звуковых колебаний большой частоты, в медицине: для разрушения камней, которые иногда образуются в организме человека, для диагностики различных заболеваний. По той же причине ультразвуковые колебания могут убивать некоторые микроорганизмы, в том числе и болезнетворные. Явление резонанса в электрических цепях при совпадении их собственных частот с частотами электромагнитных колебаний радиоволн позволяет нам при помощи своих приемников принимать теле- и радиопередачи. Резонансом при совпадении частоты электромагнитных колебаний с собственными частотами колебаний атомов можно объяснить поглощение света веществом. А это поглощение лежит в основе поглощения тепла от Солнца, в основе нашего зрения и даже в основе работы СВЧ-печи.
47

Рис. 6.7. Потеря устойчивости и разрушение моста. Собственная частота колебаний совпала с частотой вынуждающей силы
Увеличить амплитуду колебаний можно еще одним способом — изменяя подходящим образом параметр системы, например, длину нити у математического маятника, или положение центра тяжести у физического маятника. Таким способом раскачивания пользуются любители качелей (рис. 6.8). Это явление называют параметрическим резонансом.
Рис. 6.8. Параметрический резонанс. Циклически изменяется параметр системы
6.4. Сложение колебаний
Сложение колебаний равных частот,
происходящих в одном направлении
Рассмотрим тело, которое колеблется относительно стола, а стол, в свою очередь, совершает колебательные движения относительно пола, в том же направлении. Тогда если рассмотреть движение тела относительно пола, то оно будет тоже колебательным с той же частотой, но с другой амплитудой и с другой начальной фазой. Очень важное требование к этим двум колебаниям (которые мы будем складывать), — чтобы они были гармоническими, т.е. каждое колебание должно описываться законом, например, косинуса. Для решения такой задачи применяется метод векторных диаграмм. Если радиус-
вектор r вращается с угловой скоростью ω, то проекция этого вектора на ось Х будет изменяться по гармоническому закону x = r cos(ωt) (рис. 6.9, а). Если начальная фаза (фаза в момент времени t = 0) вектора амплитуды колебаний равна ϕ , то его начальное положение можно изобразить в виде рис. 6.9,
в. Тогда проекция на ось х будет изменяться по закону x = Acos(ωt + ϕ) . Если тело одновременно участвует в двух колебательных процессах, то под сложением колебаний понимают нахождение закона, описывающего результирующий колебательный процесс. Для сложения колебаний
x1 = A1 cos(ωt + ϕ1) и x2 = A2 cos(ωt + ϕ2 ) используем метод вращающегося вектора амплитуды (метод векторных диаграмм). Так как векторы A1 и A2 (рис. 6.9, б) вращаются с одинаковой угловой скоростью ω, то разность фаз ( ϕ2 − ϕ1 ) между ними остается постоянной. Уравнение результирую-
48

щего колебания будет x = x1 + x2 = Acos(ωt + ϕ0 ) , где амплитуду А и начальную фазу ϕ0 можно вычислить с помощью рис. 6.9, б.
а) |
б) |
в)
Рис. 6.9. Метод векторных диаграмм. Геометрический метод сложения двух колебаний
с одинаковыми частотами
Сложение взаимно перпендикулярных колебаний
Пусть два гармонических колебания одинаковой частоты ω происходят во взаимно перпендикулярных направлениях вдоль осей x и y. Для простоты выберем начало отсчета так, чтобы начальная фаза первого колебания была равна нулю: x = Acos(ωt) , y = Bcos(ωt + α) , где α — разность фаз колебаний, а A и B — их амплитуды. Рассмотрим три частных случая:
а) когда разность фаз равна нулю, α = 0 и y = B x (рис. 6.10, а);
A
б) когда разность фаз равна π, α = π и |
|
y = − |
B |
x (рис. 6.10, б); |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
A |
|
|
|
|
|
||
π |
|
|
π |
|
|
|
|
x2 |
y2 |
||||
в) когда разность фаз равна |
|
α = |
|
|
и уравнение траектории примет вид: |
|
|
+ |
|
|
= 1. Это |
||
|
A |
2 |
B |
2 |
|||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
||
уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам A и B (рис. 6.10, в).
в)
Рис. 6.10. Сложение взаимно перпендикулярных колебаний одинаковой частоты
Если взаимно перпендикулярные колебания происходят с циклическими частотами pω и qω , где p и q — целые числа, x = Acos( pωt), y = Bcos(qωt + α) , то значения координат x и y одновременно повторяются через одинаковые промежутки времени Т0, равные наименьшему общему кратному периодов T1 = 2π pω и T2 = 2π qω колебаний вдоль осей x и y. Траектории замкнутых кривых, которые
получаются в этих случаях, называются фигурами Лиссажу. Вид этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рис. 6.11 показан вид фигур Лиссажу
при трех различных значениях отношения частот (а — 2:1; б — 3:2; в — 4:3) и разности фаз α = π 2 .
Мы рассмотрели в общих чертах колебания некоторых физических систем, изучили основные общие закономерности колебательного процесса. Но мы не выходили за рамки линейных колебаний, ко-
49

гда возвращающая сила линейно зависит от x, по этой причине и получились такие простые гармонические колебания. Но реальные системы даже при малых амплитудах проявляют себя сложным образом — колебания становятся не гармоническими, такие системы называют нелинейными, или ангармоническими. Это может приводить к хаотическому движению, т.е. хаосу.
а) |
б) |
|
в) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.11. Фигуры Лиссажу
7. ВОЛНЫ
7.1. Волновой процесс
Глядя на волны, которые бегут по тихой поверхности воды, невольно понимаешь, что у них есть много общего с колебаниями. Волны — это колебания, которые распространяются в пространстве.
Рис. 7.1. Реальные волны на воде и в фантазии художника
Источником круговых волн, изображенных на рис. 7.1, служит доска, которая вертикально колеблется на поверхности воды. Это периодическое возмущение распространяется по поверхности воды с постоянной скоростью V, образуя волну. Система концентрических окружностей расширяется во времени со скоростью распространения волны, а количество окружностей увеличивается, причем за один период колебания доски Т появляется одно новое кольцо в точке (области) контакта доски с водой. Расстояние между двумя соседними гребнями волны называется длиной волны λ . Максимальное поднятие гребня волны над уровнем невозмущенной воды называется амплитудой волны А. Перечисленные параметры волны не независимы, они связаны между собой соотношением: λ = VT . В природе встречаются различные по масштабам волны (длина волны изменяется от миллиметров до сотен метров). Волновая картина на поверхности и в глубине океана выразительно изображена художником, масштаб течения можно оценить по размерам судна (см. рис. 7.1). Волны другой природы наблюдаются на поверхности тонкой пленки жидкости. Интересная фотография этого явления приведена на рис. 7.2 (фотография взята на сайте foto.ru). Волны образовались на всплеске воды, точнее, на стекающей пленке всплеска. На увеличенном фрагменте хорошо видны волны, которые взаимодействуют между собой.
50
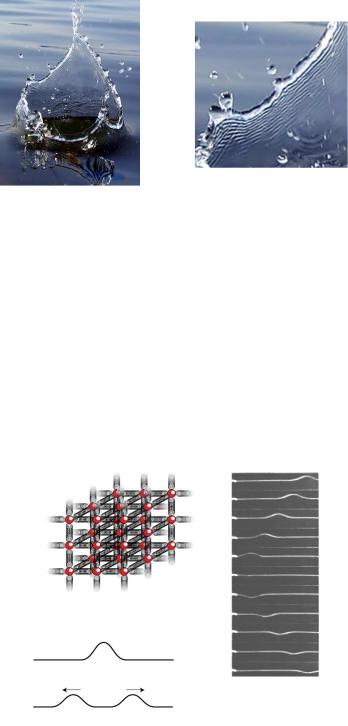
Рис. 7.2. Поверхностные волны на тонкой пленке воды (всплеск), справа — увеличенный фрагмент
Есть волны, которые распространяются в упругой среде. Упругие среды — это твердые тела, жидкости и газы. Рассмотрим, например, твердое тело. Твердое упругое тело можно представить в виде модели: система материальных точек массой m, равномерно расположенных в пространстве и соединенных невесомыми пружинками жесткостью k (рис. 7.3, а). На рисунке массы расположены в вершинах кубиков, заполняющих все пространство. В равновесном состоянии все шарики покоятся на своих местах. Если отклонить один шарик, то возникнет сила, которая будет стремиться вернуть шарик на место, это возвращающая сила. Возмущение, которое мы ввели в систему, будет передаваться от одного шарика к другому, т.е. распространяться во все стороны с некоторой скоростью, которая называется скоростью распространения возмущения. Если отклонять шарик по гармоническому закону, то во все стороны будет распространяться упругая волна. Рассмотрим одномерное упругое тело, например, резиновый жгут. Если отклонить от положения равновесия маленький элемент жгута и отпустить (рис. 7.3, в), то в обе стороны жгута будет распространяться возмущение (рис. 7.3, г). Если конец жгута закреплен, то возмущение, пришедшее к этому концу, отразится и начнет распространяться в обратном направлении (рис. 7.3, б).
а) |
б) |
в)
г)
Рис. 7.3. Модель твердого упругого тела — а; возмущение на одномерном упругом жгуте — в, г; отражение возмущения от закрепленного
конца жгута — б
На рис. 7.3, б показана последовательность процесса распространения возмущения и его отражения от закрепленного конца упругого жгута. Направление возмущения после отражения поменяло знак (смещение было вверх, стало вниз).
Мы рассмотрели волны на поверхности жидкости и волны в упругой среде. Эти волны называют бегущими волнами. Как же описать бегущую волну? Чтобы понять это, давайте сядем в неподвижную относительно берега лодку, которая качается на волнах (лодка поднимается и опускается вместе с волной, т.е. изменяет свое положение по высоте относительно спокойного уровня воды), и будем отмечать положение лодки в зависимости от времени на вертикальной оси координат y. У нас получится знакомый уже график колебаний, которые мы умеем описывать:
51
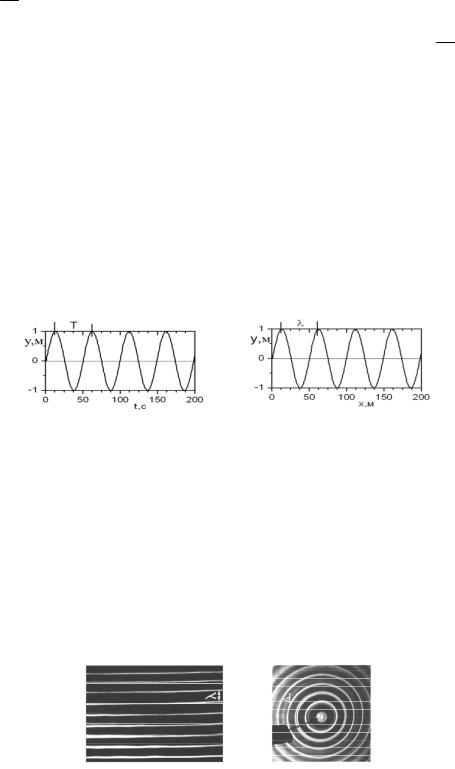
y(t) = Acos(ωt + ϕ0 ) (рис. 7.4, а). Волна, на которой качается лодка, распространяется в направ-
лении х от источника этой волны. Если в это время нас кто-нибудь сфотографирует с берега, то на фотографии мы увидим те же волны, на которых качалась наша лодка, но «замороженные» в некоторый момент времени t = t1. Если теперь провести на фотографии горизонтальную ось x и вертикальную ось y, то мы получим график, который будет отражать пространственную структуру волны в заданный момент времени t1: y(x) = Acos(k0 x + ϕ1) (рис. 7.4, б). Нам известно, что цикличе-
ская частота ω0 колебаний описывает периодичность волны во времени и связана с периодом
волны: ω0 = 2π . Подобным образом, k0 — это волновое число, оно описывает периодичность вол-
T
2π
ны в пространстве и связано с «пространственным периодом» волны λ : k0 = λ . «Простран-
ственный период» волны называется длиной волны, она равна расстоянию между соседними гребнями волны, которое прошел фронт волны за период: λ = VT . Рассмотрев внимательно графики, приведенные на рис. 7.4, замечаем, что смещение зависит и от времени: y = y(t) (x = const), и от расстояния источника волны до точки наблюдения: y = y(x) (t = const), т.е. смещение является функцией двух переменных: y = y(t, x). Объединяя обе эти зависимости, получим уравнение волны:
y(t, x) = Acos(ω0t + k0 x + ϕ0 ) .
Выражая λ через скорость волны и циклическую частоту, для k0 получим: k0 = ω0 . Тогда уравне-
V
ние волны можно записать в виде:
|
y(t, x) = Acos(ω (t − |
x |
)). |
(7.1) |
|||
|
|
||||||
|
0 |
V |
|
|
|||
|
|
|
|
|
|
||
а) |
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7.4. Зависимость смещения колебания волны от времени y(t) при постоянном значении x — а и зависимость смещения колебания волны от координаты y(x) при постоянном значении t — б
В выражении (7.1) знак «–» означает, что волна распространяется слева направо, т.е. в сторону увеличения x. Повторим значения всех величин в выражении (7.1): t — время наблюдения, x — расстояние от источника волны до точки наблюдения, ω0 — циклическая частота волны, V — ско-
рость распространения волны, y (t, x) — смещение частиц среды, в которой распространяется волна, в момент времени t в точке наблюдения x.
Уравнение (7.1) описывает распространение плоской волны. Волна распространяется вдоль координаты x, в сторону возрастания координаты. Создать такую волну можно с помощью тонкого длинного стержня, который должен колебаться на поверхности жидкости. Структура волны показана на рис. 7.5, а. Если в качестве источника колебаний использовать тонкую иглу, то будет наблюдаться круговая поверхностная волна (рис. 7.5, б).
а) |
б) |
Рис. 7.5. Плоская — а и круговая — б поверхностные волны
52
