Федеральное государственное бюджетное образовательное учреждение высшего образования

«Национальный исследовательский университет «МЭИ»

Отчёт по лабораторной работе № 6

По курсу «Изучение параметрических и непараметрических методов первичного анализа временных рядов»

Выполнил студент группы А-03-19

Муромцева Эльвира

Москва 2021

1. Моделирование временных рядов:

• смоделировать переменные: t со значениями от 1 до 100, а затем t² и t³ под именами t , t2, и t3.

• смоделировать два временных ряда, заданные формулами:

1. А-3-19 ‒ ряд E3Log(0.02*t)+VNormal(rnd(1);0;4),

2. А-1-2-3-19 ‒ ряд Е4→EXP(0.03*t)+VNormal(rnd(1);0;4.5)

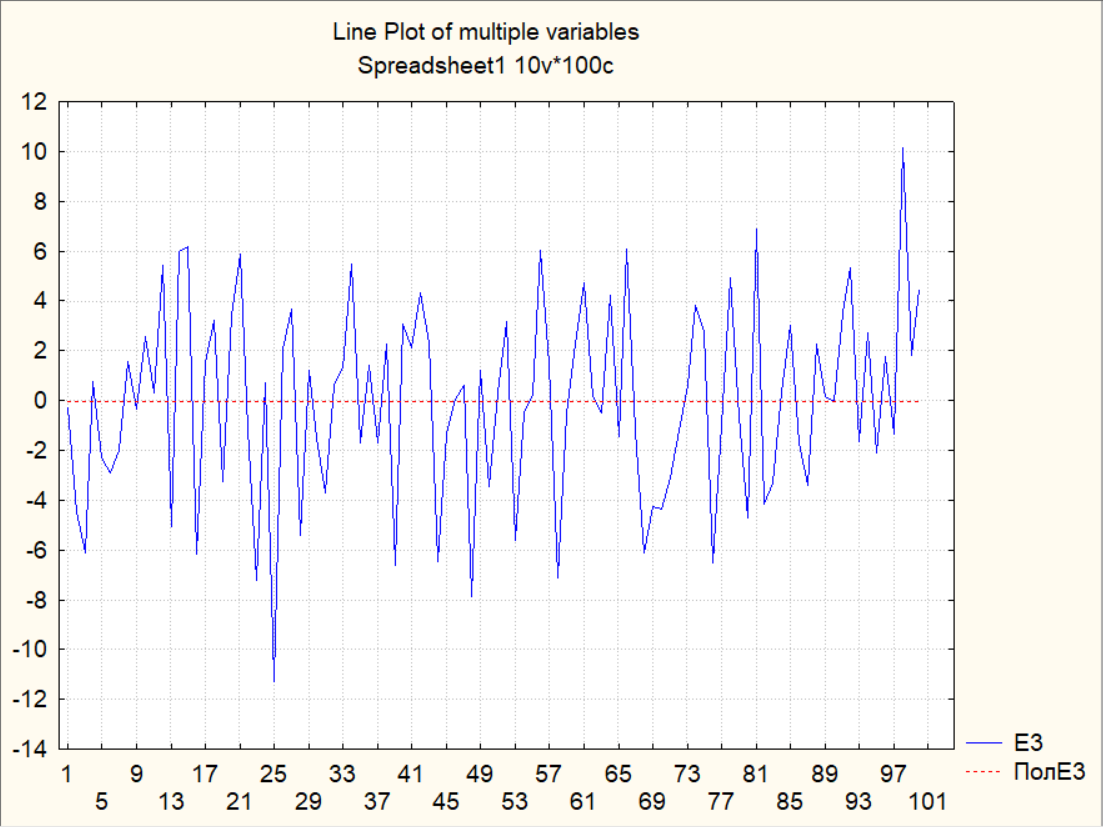
2. Построить линейные графики рядов без аппроксимации и провести визуальный анализ наличия детерминированной компоненты – тренда – во временных рядах, сделать вывод о возможности визуального определения тренда по исходной реализации.

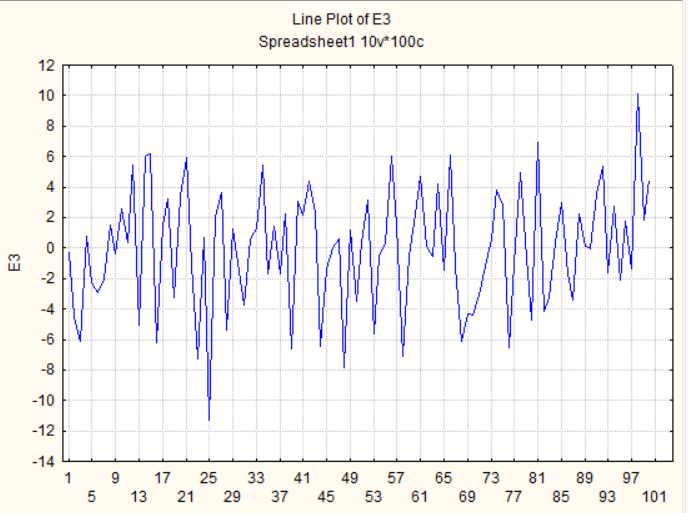
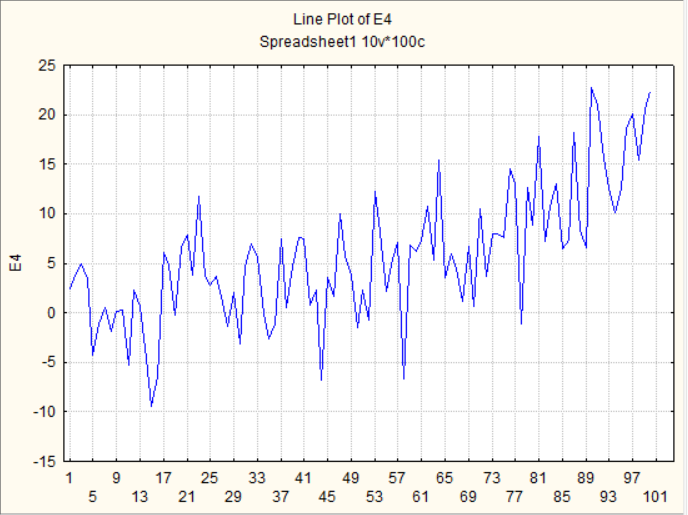
Вывод: с помощью визуального анализа можно сделать вывод об отсутствии тренда у временного ряда E3 и его наличие у E4, так как у 1-го ряда отсутствует явное возрастание значений наблюдений, в отличии от 2-го.

3. Для pяда Еi (i=1 или 2 или 3) провести поиск аномальных измерений, для этого:

• создать линейный график выбранного временного ряда с подгонкой полиномиальной функцией;

• найти и записать координаты двух выделяющихся точек, в качестве которых принять максимальное и минимальное значения; для этого:

- определить максимальное и минимальное значения в разделе «Описательные статистики»

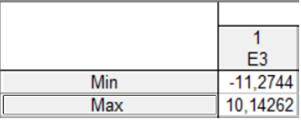
- на графиках рядов определить (хотя бы приближенно) положение этих точек

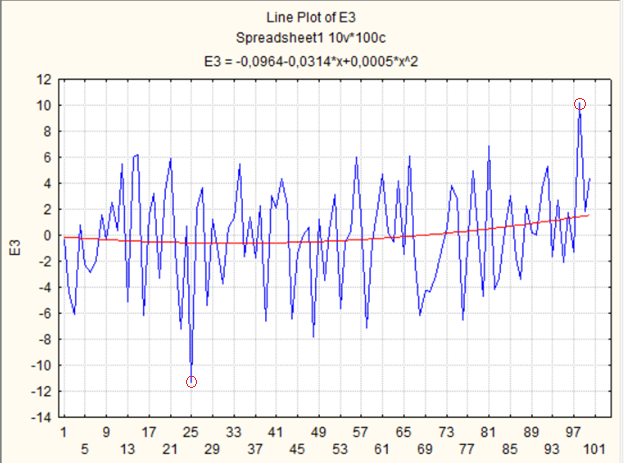
- уточнить положение (номер) точек, найдя их в таблице

4. Для исходных рядов Еi и Е4, рассчитать математические модели тренда в виде кубического полинома вида Y= b0+b1*t+b2*t^2+b3*t^3 или полинома более низкого порядка, при этом:

• для расчетов использовать модуль «Множественная регрессия» («Multiple Regression» см. раздел 2.3) в стандартном режиме, указав зависимую переменную Еi или Е4, а независимые переменные ‒ аргументы ‒ t, t2 и t3;

• получить окно с результатами вычислений – «Результаты множественной регрессии» («Multiple Regression Results») и записать в отчет аналитическое выражение для модели с учетом значимости параметров, т.е. полиномиальное описание тренда;

• при незначимых параметрах понижать степень полинома, чтобы получить полиномиальную модель порядка 2 или 1, или 0 (как среднее по ряду);

E3

Вычисление для:

Полинома 3 степени

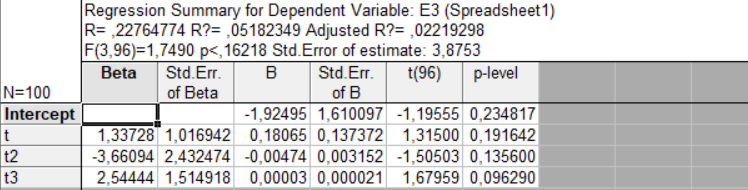
Полинома 2 степени

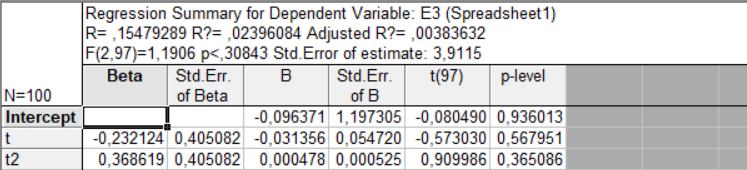
Полинома 1 степени

При вычислении оценок параметров для полиномов 1-3 степени не было получено значимых оценок, поэтому понизим степень до 0, т.е. вычислим среднее по ряду: MeanE3 = -0,0636991602

E4:

Вычисление для:

Полинома 3 степени

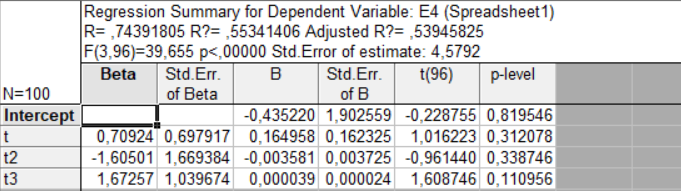
Полинома 2 степени

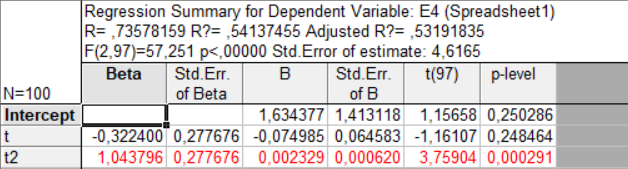
Получили значимую оценку параметра t^2, поэтому полином принимает вид:

ПолE5 = 0.002329*t^2

5. Проверить наличие минимального и максимального значений временного ряда Еi, обнаруженных в п.3, и провести их коррекцию, для чего в режиме табличного представления данных провести редактирование ряда двумя способами:

а) введя вместо максимального измерения значение, полученное линейной интерполяцией соседних измерений (полусумма соседних значений),

Max = (-1.33485+1,793567)/2=0.2293585

б) введя вместо минимального измерения соответствующее значение из полученной ранее аппроксимирующей полиномиальной зависимости.

Min = -0,693147180559945

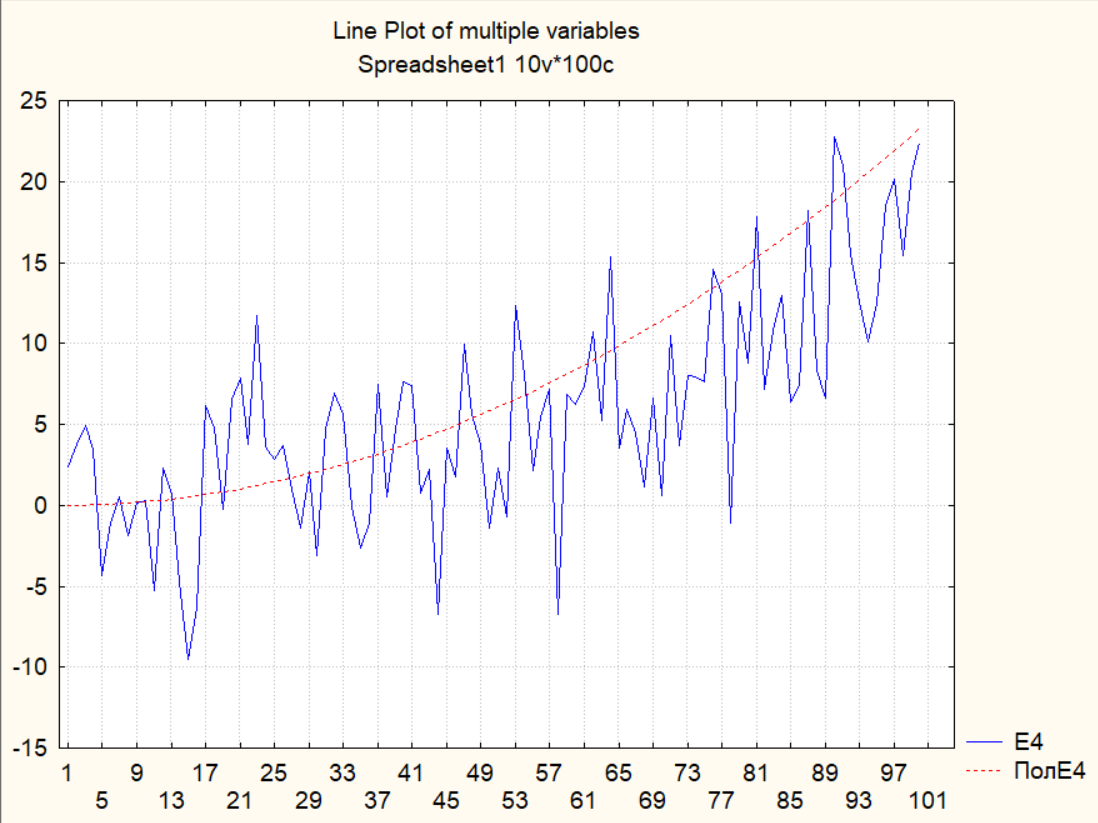
6. Построить на одном рисунке графики исходного ряда и модели тренда (Predicted Value) для обоих рядов.

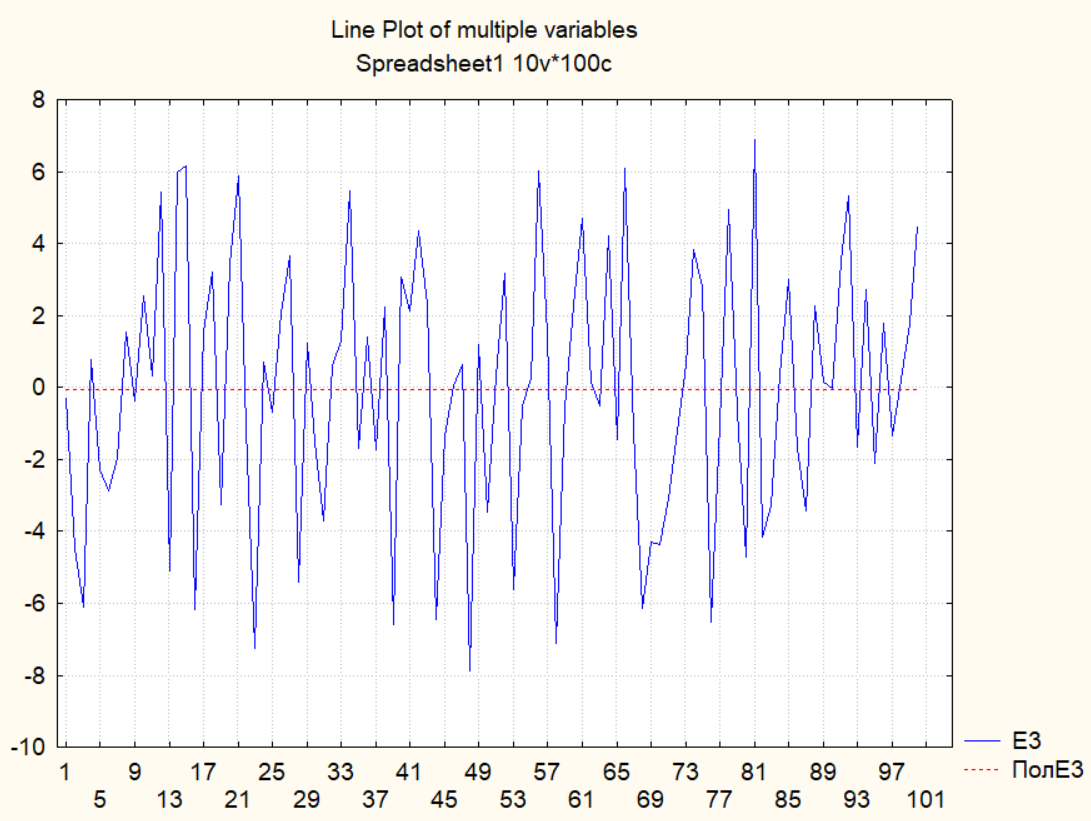
7. Провести начальный статистический анализ рядов с удаленным трендом, т.е. случайных компонент рядов.

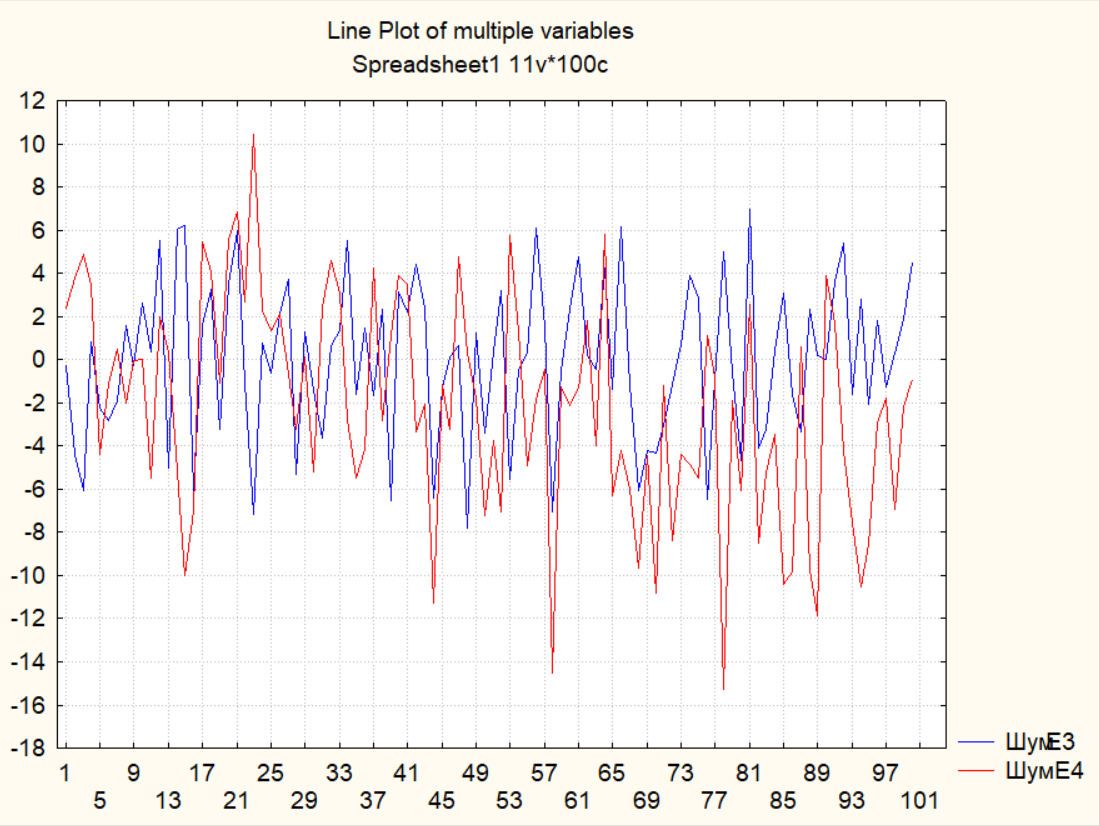
E3:

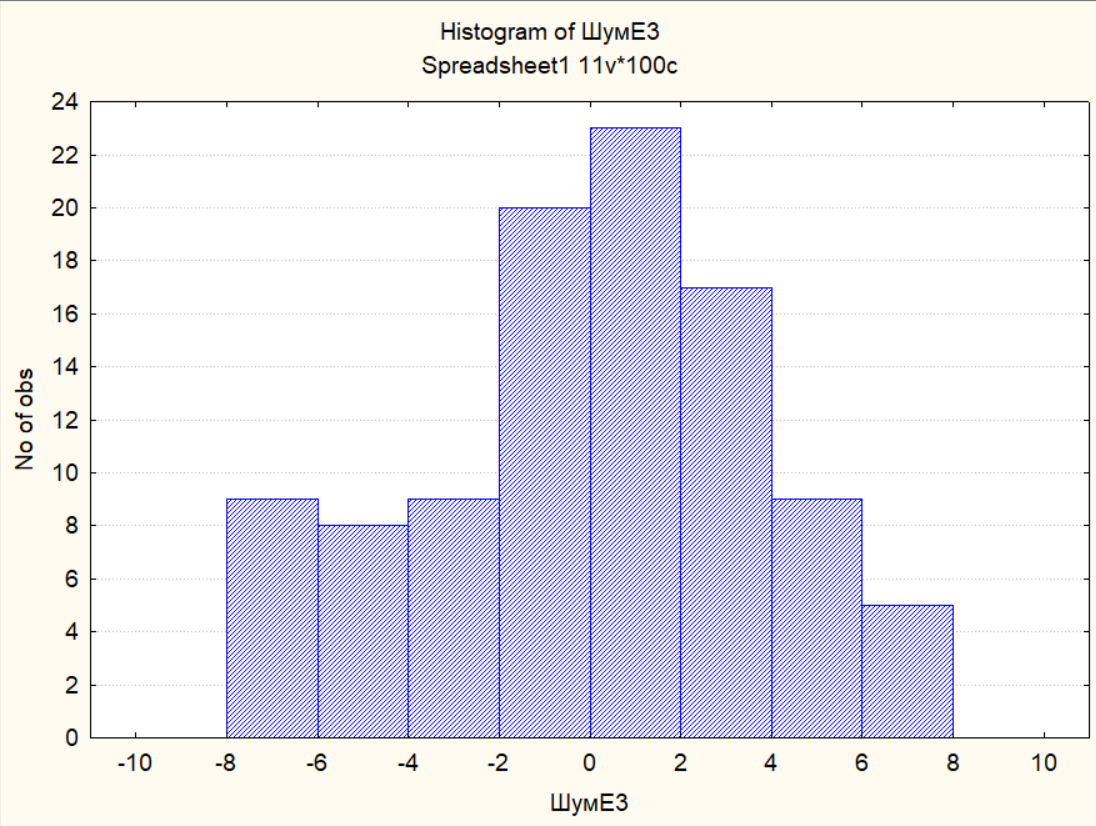
E4:

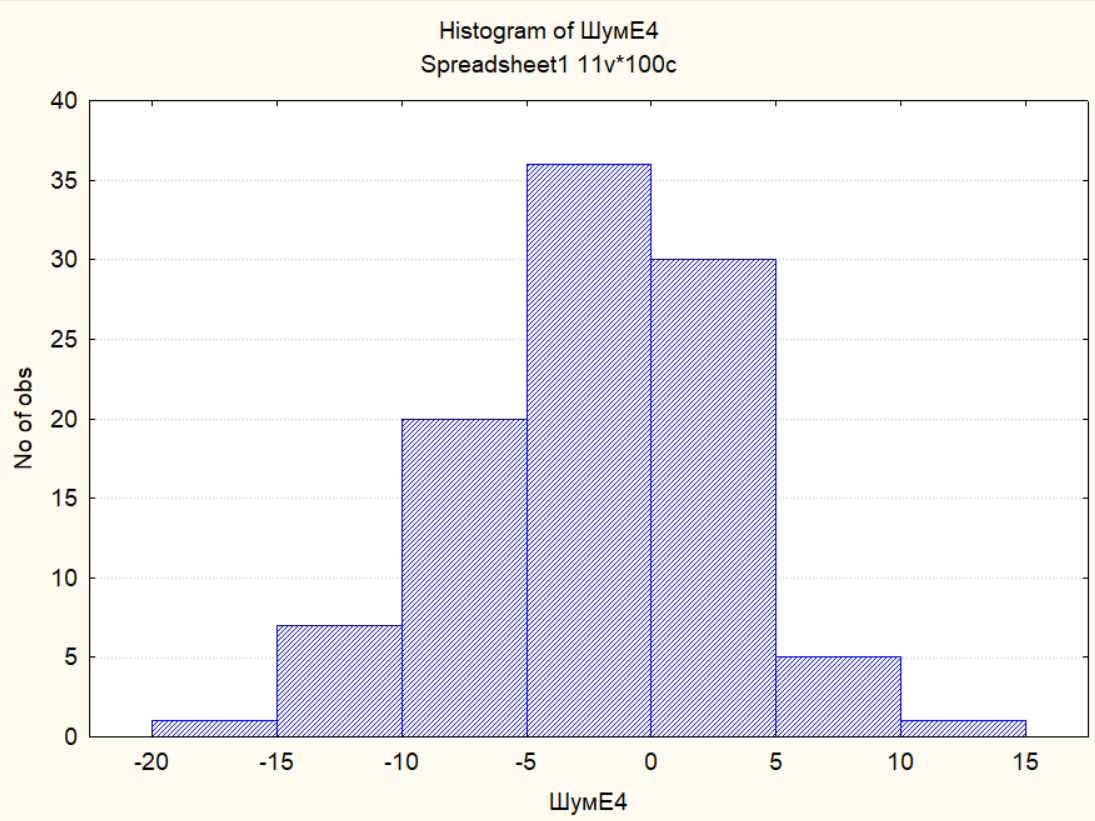
Вывод: по графикам наблюдается отсутствие тренда в рядах, но центрирование произошло только для ряда E3, так как его математическое ожидание 0, по гистограммам можно сделать вывод о том, что наблюдения ВР распределены приблизительно по нормальному закону.