
Fizicheskaya_termodinamika
.pdf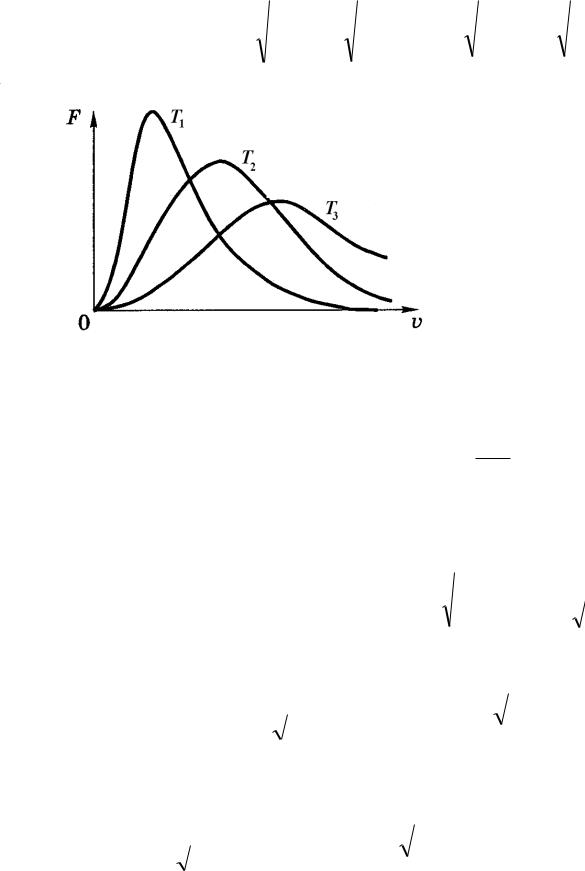
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8kT |
|
|
8RT |
|
|
|
|
4 |
|
|
|
|
|
8 |
|
|
|
|||
m |
M |
вер |
|
|
КВ |
3 . |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
увеличением температуры |
|||||||||||
|
|
|
|
|
|
|
|
|
( Т3 > T2 > T1 ) максимум |
||||||||||||
|
|
|
|
|
|
|
|
|
функции |
|
F(υ) |
|
|
смещается в |
|||||||
|
|
|
|
|
|
|
|
|
сторону |
больших |
скоростей. |
||||||||||
|
|
|
|
|
|
|
|
|
При этом доля молекул, |
||||||||||||
|
|
|
|
|
|
|
|
|
обладающих |
|
|
|
|
малыми |
|||||||
|
|
|
|
|
|
|
|
|
скоростями, уменьшается, а |
||||||||||||
|
|
|
|
|
|
|
|
|
доля |
|
молекул |
|
с |
большими |
|||||||
|
|
|
|
|
|
|
|
|
скоростями |
|
увеличивается. |
||||||||||
|
|
|
|
|
|
|
|
|
Площадь |
|
под |
|
всеми тремя |
||||||||
|
|
|
|
|
|
|
|
|
кривыми |
|
остаётся |
равной |
|||||||||
|
|
|
|
|
|
|
|
|
единице. |
|
|
|
|
|
|
|
|
||||
Аналогично закону распределения молекул по скоростям можно найти закон распределения молекул идеального газа по кинетическим энергиям их теплового
dN
движения. Это распределение устанавливает долю молекул, кинетическая
N0
|
|
|
|
|
|
|
т 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
энергия которых |
|
|
|
|
0 |
|
|
|
|
|
заключена в интервале от |
|
0 |
до |
( 0 d 0 ) . |
||||||||||||||||||||||||||
|
0 |
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Чтобы получить |
|
такое распределение |
нужно |
в |
|
|
законе Максвелла |
перейти от |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 0 |
|
|||
скорости к энергии |
0 по соотношениям |
|
|
|
2 0 |
и |
d |
|
. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
т0 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m0 0 |
|||||||
В результате получаем |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kT |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
dN |
N0 |
|
|
|
|
|
|
exp |
|
|
|
|
|
|
0 d 0 . |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kT |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Введём обозначение |
|
dN |
|
F ( 0 ) d 0 , |
где |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
N0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
kT |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
F ( 0 ) |
|
|
|
|
|
exp |
|
|
|
|
|
|
0 |
|
|
– |
|
функция |
распределения |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
молекул идеального газа по кинетическим энергиям.
По аналогии со средней скоростью найдём среднюю кинетическую энергию поступательного движения молекулы идеального газа:

32
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
||
|
0 |
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|||||||
0 |
F( |
0 )d 0 |
|
|
|
|
exp |
|
|
|
0 d 0 |
|
|
kT |
|
|||||||||
|
3 |
|
|
|
|
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kT |
|
|
|
2 |
|
|||
|
0 |
|
|
|
|
|
|
(kT)2 |
0 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
3 |
kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом |
0 |
|
, что и следовало ожидать. |
|
|
|
|
|
|
|
||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Прямые измерения скоростей теплового движения молекул были впервые выполнены в 1920 г. Штерном в опытах с молекулярными пучками спустя 60 лет после опубликования закона Максвелла.
В качестве исследуемого газа были взяты пары серебра, которое испарялось в вакууме с поверхности платиновой проволоки, нагреваемой электрическим током..
На пути атомов серебра ставился |
||||
цилиндрический экран радиусом |
RA с |
|||
узкой щелью. Атомы серебра, пролетевшие |
||||
сквозь щель, осаждались на стенке второго |
||||
цилиндра |
радиуса |
RВ , |
образуя |
узкую |
полоску |
М 0 . Если |
весь |
прибор вращать |
|
вокруг оси, совпадающей с платиновой |
||||
проволокой, то атомы серебра попадут на |
||||
стенки цилиндра RВ |
в новое место |
М . |
||
По смещению полоски и известной |
||||
угловой скорости вращения прибора можно |
||||
было вычислить скорость движения атомов |
||||
|
RB RB RA серебра |
lMM 0 – длина дуги |
|
|
|
, где |
МM0 . |
||
|
|
|||
|
lMM |
|
|
|
|
0 |
|
|
|
Найденная таким образом скорость движения атомов серебра совпала со скоростью, рассчитанной по МКТ.
Зависимость толщины слоя серебра от места конденсации атомов пропорциональна зависимости атомов в этом месте от их скорости.
Опыт Штерна хорошо согласовался с распределением молекул по скоростям Максвелла.
Барометрическая формула
Молекулы любого газа, как и любые материальные точки всегда находятся в поле тяготения Земли. Если бы не было теплового движения молекул атмосферного воздуха, то все они упали бы на Землю. Если бы не было тяготения, то атмосферный воздух рассеялся бы по всей Вселенной.

33
Для определения закона изменения давления идеального газа с высотой в однородном поле тяготения будем считать, что газ находится в состоянии термодинамического равновесия, так, что его температура Т всюду одинакова. Выделим на высоте y = h столб газа высотой dy и площадью основания S.
Давление газа на нижнее основание столба равно р , а на верхнее основание
– (р +dp). С учётом гидростатического давления ρgdy столба газа получаем
|
|
|
|
|
р ( р dp) g dy |
|
или |
dp g dy . |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
р nkT |
N |
|
kT |
NA m |
|
kT |
|
RT |
|
|
то |
pM |
|
|
||||||||||||||||||||
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
и |
|
||||||||||||||||||
V |
|
|
V M |
|
|
M |
|
RT |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
dp p |
M g |
dy |
|
|
|
|
|
dp |
|
Mg dy |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
RT |
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
RT |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Обозначив давление у поверхности Земли – р0 |
получаем после |
|||||||||||||||||||||||||||||||||||
интегрирования |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
p |
dp |
|
Mg |
h |
|
|
|
|
p |
|
|
Mgh |
|
|
|
|
|
|
|
|
|
Mgh |
|
|
RT |
|
p0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
dy ln |
|
p p |
0 |
e RT |
|
h |
ln |
||||||||||||||||||||||||||||||
p |
RT |
p |
|
|
RT |
gM |
p |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
p |
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Два последних выражения называют барометрическими формулами, позволяющими определить высоту над поверхностью Земли по показаниям барометра.
|
|
|
|
|
|
п п e |
Mgh |
|
т0 gh |
|||
|
р |
|
п |
|
|
|
RT |
п е |
|
kT |
|
|
Так как |
|
|
, то |
|
. |
|||||||
р0 |
|
п0 |
0 |
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
Если учесть, что |
m0 gh W0 – |
|
потенциальная энергия молекулы в |
|||||||||
однородном поле тяготения вблизи поверхности Земли (при условии, что на поверхности Земли W0 0 (h 0) ) то можно записать
W0
п п0 е kT
Эта формула является математическим выражением весьма общего и важного закона – Закона Больцмана для распределения частиц во внешнем потенциальном поле независимо от его физической природы.
Объединив распределения Максвелла и Больцмана получают Закон Максвелла-Больцмана, согласно которому число молекул, компоненты

|
|
|
|
34 |
скорости которых лежат |
в пределах |
от |
x ; y ; z |
до |
( x d x ); ( y d y ); ( z |
d z ) , а |
координаты |
– в пределах |
от |
x; y; z |
|
до |
(x dx); (z dy); (z dz) |
равно |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
W |
1 |
m 2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
A e |
|
|
|
|
|
d x d y d z |
|
||
dN xyz |
|
kT |
|
|
|
||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x |
y |
z |
|
|
|
|
|
|
|
|
|
|
|
, где |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A n |
0 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
– нормировочный множитель; |
|
|||||||||||||
0 |
|
2 kT |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
W W (x; y; z) |
и |
2 |
2 |
|
2 |
2 |
|
||||||||||
0 |
|
0 |
|
|
|
|
|
|
|
x |
|
|
|
y |
z |
|
|
Равновесные флуктуации
Флуктуациями называют случайные отклонения значений какого-либо параметра термодинамической системы от его среднего значения. Возникают флуктуации вследствие хаотического теплового движения частиц макросистемы
(броуновского движения).
Пусть равновесное состояние макросистемы характеризуется некоторым параметром х , среднее значение которого равно < x > . Тогда флуктуации этого параметра определятся как отклонение его значений от среднего:
х = х – < x >.
Средним квадратом флуктуации параметра х называют величину:
 (х)2
(х)2 
 (х
(х  х
х )2
)2 
 х2
х2  2
2 х
х
 х
х
 х
х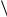 2
2  х2
х2 
 х
х 2 .
2 .
Средней квадратичной флуктуацией называют величину 

 (х)2
(х)2  .
.
Для количественной оценке флуктуаций используют среднюю
|
(х)2 |
|
квадратичную относительную флуктуацию |
х |
. |
|
|
Для всех термодинамических параметров (давление, температура, объём, внутренняя энергия, энтропия) средние квадратичные относительные флуктуации

35
(или просто относительные флуктуации) обратно пропорциональны корню из числа N частиц в системе:
(х)2 |
|
1 |
|
|
~ |
||
х |
N . |
||
|
Коэффициент пропорциональности для равновесных состояний имеет значение порядка единицы.
Статистическое обоснование второго начала термодинамики
Пусть имеются два одинаковых сосуда, соединённых между собой таким образом, что газ из одного сосуда может перетекать в другой и пусть в начальный момент все молекулы газа находятся в одном сосуде. По истечении некоторого времени произойдёт перераспределение молекул, приводящее к возникновению равновесного состояния, характеризующегося равной вероятностью нахождения молекул в обоих сосудах. Самопроизвольный переход в исходное неравновесное состояние, при котором все молекулы сосредоточены в одном из сосудов, практически невозможен. Процесс перехода из равновесного в неравновесное состояние оказывается очень маловероятным, так как размер относительных флуктуаций параметров при больших количествах частиц в сосудах очень мал.
Этот вывод соответствует второму началу термодинамики, утверждающему, что термодинамическая система самопроизвольно переходит из неравновесного состояния в равновесное, тогда как обратный процесс возможен только при внешних воздействиях на систему.
Энтропия и вероятность
Термодинамической величиной, характеризующей направление протекания самопроизвольных термодинамических процессов, является энтропия. Наиболее
вероятному равновесному состоянию соответствует максимум энтропии.
Пусть имеется сосуд объёмом V0 , внутри которого находится одна молекула. Вероятность того, что частица будет обнаружена внутри некоторого
объёма V < V0 , выделенного внутри сосуда, равна Р(1) |
V |
|
|
. Если в сосуде |
|
V |
||
0 |
||
находится не одна, а две частицы, то вероятность их одновременного обнаружения в указанном объёме определяется как произведение вероятностей нахождения в этом объёме каждой из частиц:
|
|
2 |
||
P(2) |
P(1) Р(1) |
V |
|
|
|
||||
|
|
. |
||
|
V0 |
|
||
Для N частиц вероятность их |
одновременного |
обнаружения в объёме V |
||
составит |
|
|
|
|

36
|
N |
|
P(N ) |
V |
|
|
||
|
. |
|
V0 |
|
|
Если в этом сосуде выделить два объёма V1 и V2 то можно записать отношения вероятностей того, что все молекулы находятся в указанных объёмах:
Р2 |
|
N |
|
|
V2 |
|
|
|
|
||
Р1 |
|
. |
|
V1 |
|
||
Определим приращение энтропии в изотермическом процессе
Q A RTV dV
расширения идеального газа от V1 до V2 :
2 |
Q |
V2 |
dV |
|
|
|
|
||
|
|
|
|||||||
S S2 S1 |
R |
V2 |
|
|
V2 |
||||
|
|
R ln |
|
|
N A |
k ln |
|
||
T |
V |
|
|
||||||
1 |
V |
V1 |
|
|
V1 |
||||
|
|
1 |
|
|
|
|
|
|
|
Используя отношение, вероятностей получаем:
|
|
|
|
|
V2 |
|
||
|
N k ln |
|
|
V1 |
|
|
|
|
|
|
V2 |
|
||
|
k ln |
|
|
V1 |
|
|
|
Р2 |
|
|
S S2 S1 |
|
|
||
|
||||
k ln |
Р1 |
|
||
|
|
. |
Полученное выражение не определяет абсолютное значение энтропии в каком-либо состоянии, а только даёт возможность найти разность энтропий в двух различных состояниях.
Для однозначного определения энтропии используют статистический вес G, значение которого выражается целым положительным числом и пропорционально вероятности: G ~ P .
Статистическим весом макросостояния называется величина, численно равная количеству равновесных микросостояний, с помощью которых может быть реализовано рассматриваемое макросостояние.
Переход к статистическому весу позволяет записать соотношение для энтропии в виде формулы Больцмана для статистической энтропии:
N
S k ln G
.
37
Лекция 15
Явления переноса
Термодинамические потоки
Термодинамические потоки, связанные с переносом вещества, энергии или импульса из одной части среды в другую, возникают в случае, если значения тех или иных физических параметров отличаются в объёме среды.
Диффузией называют процесс самопроизвольного выравнивания концентраций веществ в смесях. Скорость диффузии сильно зависит от агрегатного состояния вещества. Быстрее диффузия происходит в газах и очень медленно в твёрдых телах.
Теплопроводностью называют явление, приводящее к выравниванию температуры в различных точках среды. Большая теплопроводность металлов связана с тем, что в них перенос теплоты осуществляется не вследствие хаотического движения атомов и молекул, как, например, в газах или жидкостях, а свободными электронами, имеющими гораздо большие скорости теплового движения.
Вязкостью или внутренним трением называют процесс возникновения силы сопротивления при движении тела в жидкости или газе и затухания звуковых волн при прохождении их через различные среды.
Для количественного описания термодинамического потока вводят величину
J j dS
, где
S
j – плотность термодинамического потока;
dS – вектор элементарной площадки, численно равный элементарной
поверхности dS и направленный по нормали к этой поверхности. |
||
|
|
|
Если термодинамический поток однороден то J j |
S . |
|
В случае диффузии поток J N |
определяет интенсивность переноса частиц |
|
примеси. |
|
|
При теплопроводности величина |
JQ численно равна количеству теплоты, |
|
переносимому за единицу времени. |
|
|
Для явления вязкости величина |
J р характеризует перенос импульса. |
|

38
Если рассматриваемая термодинамическая система находится в состоянии близком к равновесию, то плотность термодинамического потока пропорциональна градиенту соответствующей физической величины в той же точке.
|
|
|
|
|
|
|
|
|
|
Описание явлений переноса в газах |
|
|
|
|
|
|
|
|
||||||||||||||
|
Рассмотрим диффузию примеси |
одного газа с |
концентрацией |
п1 |
и |
|||||||||||||||||||||||||||
плотностью |
1 в другом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
J N1 |
DS |
dn1 |
|
и |
J 1 DS |
d 1 |
, где |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
dx |
dx |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
D |
1 |
|
|
– |
коэффициент диффузии. Единицей измерения в СИ является м2/с. |
|||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
С учётом выражений для длины свободного пробега |
|
|
|
|
и средней |
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
п 2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
8kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
скорости |
|
|
|
|
|
получаем для коэффициента диффузии: |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
m0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
1 |
|
|
4kT |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 п |
m |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Видно, что коэффициент диффузии возрастает с повышением температуры |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
D ~ |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
и уменьшается при увеличении концентрации молекул |
|
D ~ |
|
. |
||||||||||||||||||||||||||||
|
n |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Последнее связано с уменьшением длины свободного пробега, что приводит к более частым соударениям диффундирующих частиц с молекулами газа.
|
|
При описании теплопроводности в качестве переносимой величины |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
kT , которая при |
|||||||
выступает |
энергия теплового движения молекулы газа |
|||||||||||||||||||
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
наличии градиента температуры зависит от координаты х . |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
JQ S |
dТ |
|
, |
где |
|
|
||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
cV |
cV |
|
|
4m0kT |
|
|
|
|
|
|
||||||
3 |
3 |
|
|
|
– |
теплопроводность. Единицей |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
теплопроводности в СИ является Вт/(м.К). |
|
|
|
|
|
|||||||||||||||
сV |
– удельная теплоёмкость газа при постоянном объёме, Дж/(кг.К); |
|||||||||||||||||||
|
п т0 |
– плотность газа. |
|
|
|
|
|
|||||||||||||

39
При описании вязкости газа в качестве переносимой величины выступает
импульс молекулы |
т0и при упорядоченном движении газа в направлении, |
||||||||||||
перпендикулярном оси ОХ. Поток импульса |
|||||||||||||
|
|
|
|
|
|
|
|
J S |
du |
|
|||
|
|
|
|
|
|
|
|
dx , где |
|||||
|
|
|
|
|
|
|
|
|
p |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
и – скорость упорядоченного движения молекул; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
4т0kT |
|
|
– вязкость. Единицей вязкости в СИ является |
|||
3 |
3 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||
паскаль-секунда (Па.с). При нормальных условиях вязкость газов ~ 10 5 Па.с.
Величина J p представляет собой силу, с которой взаимодействуют слои
газа, двигающиеся в перпендикулярном оси ОХ направлении.
Температурная зависимость вязкости аналогична соответствующей
зависимости для теплопроводности: ~ 
 Т . От концентрации молекул (плотности газа) вязкость и теплопроводность не зависят.
Т . От концентрации молекул (плотности газа) вязкость и теплопроводность не зависят.
Между коэффициентами переноса существуют общие соотношения
cV сV D .
Полученные соотношения дают возможность по экспериментально
измеренным значениям , , D определять длину свободного пробега молекулы газа λ и её эффективное сечение σ.
Эффузия в разреженном газе
Эффузией называют процесс истечения разреженного газа из отверстия, характерные размеры которого много меньше длины свободного пробега молекул.
Пусть имеется заполненный разреженным газом сосуд, разделённый перегородкой с небольшим отверстием. Размер отверстия и толщина перегородки намного меньше длины свободного пробега молекул газа.
Если стенки одной части сосуда поддерживать при температуре Т1 , а другой – при температуре Т2 , то плотность потока
молекул из первой части сосуда во вторую и наоборот можно определить по формулам

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
j1 |
1 |
|
1 |
n1 |
|
|
p1 |
|
|
|
|
|
2 |
|
|
j2 |
1 |
2 |
n2 |
|
p2 |
|
2 |
|
|
|||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
9 m0k |
|
и |
6 |
|
|
|
|
|
|
9 m0k . |
|||||||||||||||
|
|
|
T1 |
|
|
|
|
|
T2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Если газ в двух частях сосуда находится |
в равновесии |
то |
j1 j2 и |
|||||||||||||||||||||||||||||||||
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
p1 |
|
|
|
|
p2 |
|
|
|
p |
p |
|
при |
Т |
|
Т |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
2 . |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
T1 |
|
|
|
|
|
T2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Видно, что условие равновесия для разреженного газа существенно отличается от условия равновесия для неразреженного газа, длина свободного пробега молекул которого много меньше характерного размера отверстия в перегородке сосуда. Для неразреженного газа равновесие наступает при равенстве давлений в обеих частях сосуда.
Физический вакуум
Когда длина свободного пробега молекул превышает характерный размер сосуда, говорят, что достигнут вакуум, и газ находится в состоянии
ультраразряжения.
Поведение ультраразреженного газа существенно отличается от поведения газов при обычных условиях. Отсутствует внутреннее трение (вязкость) и
теплопроводность газа. |
l может иметь место в |
Вакуум – понятие относительное: условие |
|
малых порах даже при атмосферном давлении. |
|
В технике обычно принимают l 0,1 м. |
|
Мерой степени разрежения газа служит отношение средней длины свободного пробега молекул газа и характерного линейного размера сосуда, в
котором находится газ: |
|
|
l – |
|
|
|
|
||
|
|
|
|
низкий вакуум |
|
||||
|
|
|
|
~ l |
– средний вакуум |
|
|||
|
|
|
l |
– |
высокий вакуум. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
Характеристика |
|
|
|
|
Вакуум |
|
||
|
Давление, |
|
|
низкий |
|
средний |
высокий |
сверхвысокий |
|
|
мм. рт. ст. |
|
|
760 – 1 |
|
1 – 10-3 |
10-3 – 10-8 |
10-8 и менее |
|
|
Концентрация, |
|
|
|
|
|
|
|
|
|
м-3 |
|
|
1025 – 1022 |
|
1022 - 1015 |
1019 – 1014 |
1014 и менее |
|
|
Зависимость |
от |
|
Не зависит |
Определя- |
Прямо про- |
Теплопровод- |
||
|
давления коэффи- |
|
|
от |
|
|
ются пара- |
порциональ- |
ность и вяз- |
|
циентов , |
|
|
давления |
|
метром |
ны |
кость практи- |
|
|
|
|
|
|
|
|
/ l |
давлению |
чески отсутс- |
|
|
|
|
|
|
|
|
|
твуют |
