4.2.2. Операции с полиномами
1. Представление полинома р(х) = аn хn + an−1 xn−1+ ... + а2 x2 + а1 х + а0 в MATLAB осуществляется следующим образом: p=[ аn an-1... а2 а1 а0]. Также возможно построение многочлена по заданным корням (при помощи функции poly). Создайте два полинома пятой степени двумя способами.
Для символьного отображения полинома по вектору заданных коэффициентов служит команда poly2sym:
>> c=[1 2 3 4 5];
>> poly2sym(c) % вектор коэффициентов может быть непосредственно введен в poly2sym:
ans = 1*x^4+2*x^3+3*x^2+4*x+5.
2. Умножение и деление полиномов осуществляются при помощи функций conv и dconv соответственно. Произведите обе эти операции над созданными полиномами. Для помощи по синтаксису функций используйте команду help.
3. Приближение данных полиномом осуществляется с использованием функции polyfit(x, y, n), где x и y – это заданные значения аргумента и функции, n – порядок полинома. Выполните приведенный пример приближения данных полиномом третьего порядка:
>> x=1:7; % заданный аргумент
>> y=[15, 10, 2, 47, 23, 78, 10]; % заданная функция
>> p=polyfit(x,y,3); % формирование полинома
>> x2=1:0.1:7; % точки для построения полинома
>> y2=polyval(p,x2); % вычисление значений функции
>> plot(x,y,x2,y2) % построение результата
4.2.3. Задание на самостоятельную работу
1. Вычислите в соответствии с вариантом:
1) |
|
6) |
|
2) |
|
7) |
|
3) |
|
8) |
|
4) |
|
9) |
|
5) |
|
10) |
|
)
)
)
2. Аппроксимируйте с наименьшей среднеквадратической ошибкой полиномом произвольного порядка зависимость a sin(kx)+bcos(lx) y на интервале от 0 до 2π. Значения коэффициентов возьмите из табл. 4.2.
Таблица 4.2
Коэффициенты |
Номер варианта |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
a |
1 |
3 |
2 |
8 |
5 |
10 |
9 |
4 |
6 |
7 |
b |
2 |
4 |
3.5 |
15 |
3 |
25 |
1.4 |
7 |
13 |
29 |
k |
1 |
2 |
3.1 |
2.2 |
0.7 |
2.3 |
4.5 |
2 |
1 |
0.8 |
l |
0.5 |
0.6 |
5 |
8 |
1.5 |
0.2 |
3 |
1.6 |
5 |
3 |
Формула для вычисления среднеквадратической ошибки для двух векторов x1 и x2 длиной n:
4.3. Содержание отчета
Отчет должен содержать цель лабораторной работы, краткое описание и синтаксис используемых команд, результаты выполнения всех пунктов программы работы.
Лабораторная работа 5 Введение в среду моделирования matlab Simulink
Цель работы: знакомство с основными возможностями среды MATLAB Simulink. Получение базовых навыков создания моделей в среде MATLAB Simulink.
5.1. Основные сведения
Simulink – полностью интегрированная с MATLAB графическая среда, предназначенная для моделирования и анализа динамических систем. Модель системы в среде MATLAB Simulink представляется в виде блочно-функциональной схемы. Создание моделей осуществляется перемещением в рабочую область редактора стандартных блоков из библиотеки, настройки их параметров и связей между ними. К основным достоинствам Simulink можно отнести широкий выбор стандартных блоков, возможность создания пользовательских блоков, гибкие настройки среды моделирования.
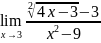
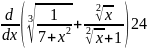
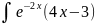