9

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Факультет безопасности (ФБ)

Кафедра безопасности информационных систем (БИС)

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Отчёт по лабораторной работе 4

по дисциплине «Численные методы»

		Студент гр.731-2
		__________ Батаев А.С.
		11.11.2022
		Руководитель: Доцент кафедры КИБЭВС
		__________ __________ Якимук А.Ю.
		11.11.2022

Томск 2022

Оглавление

Y

1 Введение 3

2 Ход работы 4

2.1 Вычисление интеграла 4

2.2 Метод левого прямоугольника 4

2.3 Метод правого прямоугольника 4

3 Заключение 6

1 Введение

Вариант:

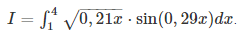
Рисунок 1.1 – Вариант

Необходимо рассчитать значение данного интеграла следующими методами: 1) методом левых прямоугольников; 2) методом правых прямоугольников; 3) методом трапеций; 4) методом Симпсона.

Листинг программы представлен в Приложении А.

2 Ход работы

2.1 Вычисление интеграла

Для дальнейшей проверки, посчитаем интеграл:

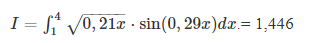
2.2 Метод левого прямоугольника

.

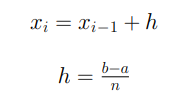
Где h – шаг сетки.

Формула метода левых прямоугольников:

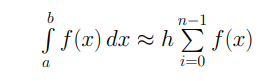
2.3 Метод правого прямоугольника

Формула метода правых прямоугольников:

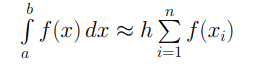
2.4 Метод трапеций

Формула метода трапеций:

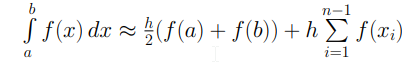
2.5 Метод Симпсона

Формула метода Симпсона:

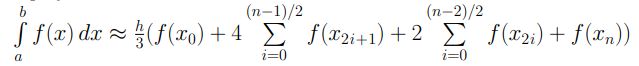
2.6 Результат работы программы

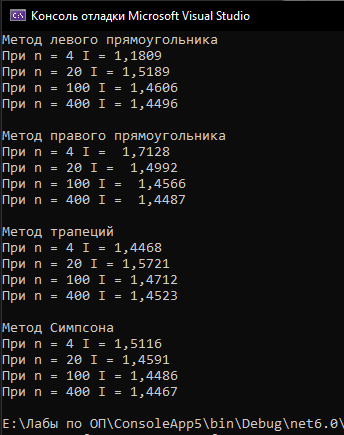
Рисунок 1– Скриншот работы программы

Таблица 1 - Результаты

Метод	X=4	X=20	X=100	X=400
Метод левого прямоугольника	1.1809	1.5189	1.4606	1.4496
Метод правого прямоугольника	1.7128	1.4992	1.4566	1.4487
Метод трапеций	1.4468	1.5721	1.4712	1.4523
Метод Симпсона	1.5116	1.4591	1.4486	1.4467

3 Заключение

В результате выполнения данной лабораторной работы были получены навыки разработки программ, использующих в своей работе методы левых, правых прямоугольников, а также метод трапеций и метод Симпсона.

Приложение A

(Обязательное)

Код приложения

namespace chm4

{

class Program

{

const double a = 1;

const double b = 4;

public static int[] n = {

4,

20,

100,

400

};

static void Main(string[] args)

{

MethodLeft();

MethodRight();

MethodTrapeze();

MethodSimpson();

}

static double Function(double x)

{

return Math.Sqrt(0.21 * x) * Math.Sin(0.29 * x);

}

static void MethodLeft()

{

Console.WriteLine("Метод левого прямоугольника");

double I, h;

for (int i = 0; i < 4; i++)

{

h = (b - a) / n[i];

I = 0;

for (double x = a; x < b; x += h)

{

I += Function(x);

}

I *= h;

Console.WriteLine($"При n = {n[i]} I = {Math.Round(I, 4)}");

}

}

static void MethodRight()

{

Console.WriteLine();

Console.WriteLine("Метод правого прямоугольника");

double I, h;

for (int i = 0; i < 4; i++)

{

h = (b - a) / n[i];

I = 0;

for (double x = a + h; x <= b; x += h)

{

I += Function(x);

}

I *= h;

Console.WriteLine($"При n = {n[i]} I = {Math.Round(I, 4)}");

}

}

static void MethodTrapeze()

{

Console.WriteLine();

Console.WriteLine("Метод трапеций");

double summ, h, I;

for (int i = 0; i < 4; i++)

{

h = (b - a) / n[i];

summ = 0;

for (double x = a + h; x < b; x += h)

{

summ += Function(x);

}

I = h / 2 * (Function(a) + Function(b)) + h * summ;

Console.WriteLine($"При n = {n[i]} I = {Math.Round(I, 4)}");

}

}

static void MethodSimpson()

{

Console.WriteLine();

Console.WriteLine("Метод Симпсона");

double x, h, summ1, summ2, I;

for (int z = 0; z < 4; z++)

{

h = (b - a) / n[z];

I = summ2 = summ1 = 0;

for (int i = 0; i <= (n[z] - 1) / 2; i++)

{

x = a + (2 * i + 1) * h;

summ1 += Function(x);

}

for (int i = 0; i <= (n[z] - 2) / 2; i++)

{

x = a + 2 * i * h;

summ2 += Function(x);

}

I = h / 3 * (Function(a) + 4 * summ1 + 2 * summ2 + Function(b));

Console.WriteLine($"При n = {n[z]} I = {Math.Round(I, 4)}");

}

}